Пусть имеется n наблюдений разбитых на m однородных групп, внутри каждой из которых предполагается одинаковая дисперсия. В этом случае сначала модель оценивают обычным МНК и находят остатки. По остаткам внутри каждой группы оценивают дисперсии 
ошибок групп как отношение сумм квадратов остатков к количеству наблюдений в группе. Далее данные каждой j-й группы наблюдений делятся на 
и к преобразованным подобным образом данным применяется обычный МНК для оценки параметров.
Если случайные ошибки подчиняются AR(1) модели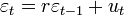 
, то без учета первого наблюдения преобразование P будет заключаться в следующем: из текущего значения переменных отнимаются предыдущие, умноженные на 
:
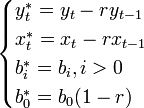
Данное преобразование называется авторегрессионным преобразованием. Для первого наблюдения применяется поправка Прайса — Уинстена — данные первого наблюдения умножаются на 
. Случайная ошибка преобразованной модели равна 
, которая по предположению есть белый шум. Следовательно применение обычного МНК позволит получить качественные оценки такой модели.
Поскольку коэффициент авторегрессии неизвестен, то применяются различные процедуры доступного ОМНК.
Процедура Кохрейна-Оркатта.
Шаг 1. Оценка исходной модели методом наименьших квадратов и получение остатков модели.
Шаг 2. Оценка коэффициента автокорреляции остатков модели (формально её можно получить также как МНК-оценку параметра авторегрессии во вспомогательной регрессии остатков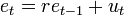 
)
Шаг 3. Авторегрессионное преобразование данных (с помощью оцененного на втором шаге коэффициента автокорреляции) и оценка параметров преобразованной модели обычным МНК.
Оценки параметров преобразованной модели и являются оценками параметров исходной модели, за исключением константы, которая восстанавливается делением константы преобразованной модели на 1-r. Процедура может повторяться со второго шага до достижения требуемой точности.
Процедура Хилдрета — Лу.
В данной процедуре производится прямой поиск значения коэффициента автокорреляции, которое минимизирует сумму квадратов остатков преобразованной модели. А именно задаются значения r из возможного интервала (-1;1) с некоторым шагом. Для каждого из них производится авторегрессионное преобразование, оценивается модель обычным МНК и находится сумма квадратов остатков. Выбирается тот коэффициент автокорреляции, для которого эта сумма квадратов минимальна. Далее в окрестности найденной точки строится сетка с более мелким шагом и процедура повторяется заново.
Процедура Дарбина.
Преобразованная модель имеет вид:
Раскрыв скобки и перенеся лаговую зависимую переменную вправо получаем
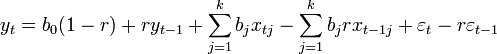
Введем обозначения 
. Тогда имеем следующую модель
Данную модель необходимо оценить с помощью обычного МНК. Тогда коэффициенты исходной модели восстанавливаются как 
.
Список литературы.
1. Айвазян С.А, Мхитарян В.С. Прикладная статистика и основы эконометрики: Учебник. – М.: ЮНИТИ, 1998. – 1022 с.
2. Катышев П.К, Пересецкий А.А. Сборник задач к начальному курсу эконометрики. – М.: Дело, 1999. – 72 с.
3. Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов / Под ред. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА, 2002. – 311 с.
4. Магнус Я.Р, Катышев П.К, Пересецкий А.А. Эконометрика. Начальный курс: Учебник для экон. спец. - М.: Дело, 2000. – 400 с.
5. Практикум по эконометрике: Учебное пособие / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2001. – 192 с.
6. Унифицированные методические указания по написанию и оформлению рефератов, контрольных, курсовых и дипломных работ для студентов БИЭФ /Составитель Э.С. Круглова. – Калининград: БИЭФ, 2003. – 42 с.
7. Эконометрика: Учебник для вузов / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2001. – 344 с.