Контрольная работа
По дисциплине: Эконометрика
Работу выполнила
студентка группы 15-ВФК-М
Левченко Яна Александровна
«___» ____________ 2015 г.
Работу проверил
к.э.н., доцент
Настин Юрий Яковлевич
«___» ____________ 2015 г.
Калининград
Содержание
1. Задача №1. Линейная парная регрессия. 3
2. Задача №2. Множественный регрессионный анализ. 10
3. Теоретические вопросы.. 19
3.1 Коэффициент ранговой корреляции Спирмена. 19
3.2 Обобщённый метод наименьших квадратов. 22
Список литературы.. 27
Задача №1. Линейная парная регрессия.
1.1. Нанести в координатах ХY точки на плоскость (построить корреляционное поле).
Решение. Для наглядности выберем наши данные из табл.1. в табл. 3.
Таблица 3
| xi | |||||||
| yi |
На рис. 1 представлено корреляционное поле. Как видно, оно должно хорошо аппроксимироваться прямой линией. Зависимость между Х и Y тесная и прямая.
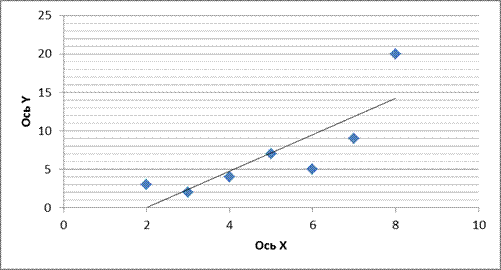
Рис.1
1.2. Найти методом наименьших квадратов уравнение регрессии Y по Х в линейной форме:
 =b0+ b1x.
| (1) |
Решение. Расчетные формулы для неизвестных параметров регрессии:
(2)
На основе табл. 3 рассчитаем необходимые суммы, входящие в формулу (2).
Таблица 4
| xi | yi | x2 | xiyi | (xi-  )2
|  xi
| ei2=( xi-yi)2
|
| 0,06 | 8,644 | |||||
| 2,42 | 0,176 | |||||
| 4,78 | 0,608 | |||||
| 7,14 | 0,02 | |||||
| 9,5 | 20,25 | |||||
| 11,86 | 8,18 | |||||
| 14,22 | 33,41 | |||||
| 71,29 |
= 5; ȳ = 7,14; 
= 45,14;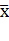 
2 = 29 (3)
Искомые оценки параметров регрессии и само уравнение регрессии:
b1 = (45,14-(5,7,14))/29-25 = 9,44/4=2,36
|
|
b0 = 4,14-2,26*5=-4,66
= 2,36*5-4,66=11,8-4,66=7,14.
1.3. Построить линию регрессии на координатной плоскости XY.
Решение. Искомую линию проще всего построить по двум точкам (см. рис. 1), например (2; 0,06) и (8,00; 14,22).
1.4. Показать графически и аналитически, что линия регрессии проходит через точку (
, 
).
Решение. Из графика на рис.1 видно, что линия регрессии проходит через точку “средних” ( =5; =7,14). Проверим это аналитически: =2,36*5-4,66= 7,14, что и требовалось доказать.
1.5. На сколько вырастет средний объем продаж при увеличении х на 1.
Решение. При увеличении торговой площади на 1 (100 м2) в среднем объем продаж увеличится на b1= 2,36 (т.е. на 23600 руб./день).
1.6. Имеет ли смысл свободный член в уравнении регрессии.
Решение. Свободный член b0=-4,66 смысла не имеет, т.к. при нулевой торговой площади положительного объема продаж быть не может.
1.7. Вычислить коэффициент корреляции между переменными X и Y.
Решение. Используем формулу:
(4)
Здесь известно все, кроме
S2y= 83,43- 7,142 = 32,45; Sy = 5,70
S2х = 29-25= 4; Sх = 2
Окончательно rxy = (45,14 – 5*7,14)/5,7*2 = 9,44/11,4 = 0,83
Полученное значение коэффициента корреляции говорит о высокой (почти функциональной) зависимости объема продаж от размера торговой площади.
1.8. Определить графически и аналитически прогнозное среднее значение объема продаж для проектируемого магазина "СИ" с торговой площадью х=11 (напомним, что это 1100 м2).
Решение. Прогнозное значение из рис.1 и из формулы совпадают:
=2,36*11 – 4,66 = 21,3 (213000 руб./день)
1.9, а) Найти 95%-ный доверительный интервал для среднего прогнозного значения объема продаж.
Решение. Оценка значения условного МО Мх=11(Y) равна 21,3. Чтобы построить доверительный интервал для СВ х=11, нужно оценить дисперсию ее оценки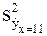 
.
|
|
Для этого определим дисперсию возмущений (см. табл. 4, графы 4-6):
S2 = 71,29/(7-2) = 14,26; S= 3,78.
Искомая дисперсия
S2 х=11 = 14,26* 
+ 
= 20,4; S х=11 = 4,52
Для статистики Стьюдента 
число степеней свободы k = n – 2 = 7 – 2 = 5. По табл. П2 находим значение t0,95;5=2,57 критерия Стьюдента. Искомый 95%-ный доверительный интервал для среднего прогнозного значения объема продаж магазина "СИ":
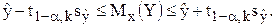
Нижнее значение интервала: 21,3-2,57*4,52 = 9,68.
Верхнее значение интервала: 21,3 + 2,57*4,52 = 32,92.
Окончательно интервал имеет вид:
9,68 £ Mx(Y) £ 21,3.
1.9, б). Найти 95%-ный доверительный интервал для индивидуального прогнозного значения объема продаж xo=11.
Решение. Чтобы построить доверительный интервал для СВ хo=11, нужно оценить ее дисперсию:
S2 х=11 =14,26*(1+1/7+36/28)=14,26*2,43=34,65; S х=11 =5,89.
Нижнее значение интервала: 21,3-2,57×5,89=6,16.
Верхнее значение интервала: 21,3+2,57×5,89=36,44.
Окончательно интервал имеет вид:
6,16 £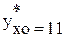 
£ 36,44.
Как и следует из теории, этот интервал больше предыдущего и большой по величине. Коэффициент осцилляции для него:
Ко=(R/ 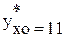)100%= ((36,44 – 6,16)/21,3)100%=142%.
1.10, а) Найти с надежностью 0,95 интервальные оценки коэффициента регрессии b1.
Решение. Общая формула для расчета интервала:
b1-D £ b1 £ b1+D,
где D = 2,57*3,78/(
)=1,84.
Нижнее значение интервала: 2,36-1,84=0,52.
Верхнее значение интервала: 2,36+1,84=4,2.
Окончательно интервал имеет вид:
0,52 £ b1 £ 4,2.
1.10, б) Найти с надежностью 0,95 интервальные оценки дисперсии возмущений s2.
Решение. Найдем по табл.П3 (критерий Пирсона) табличное значение статистики хи-квадрат: 
|
|
Формула для доверительного интервала
s2нижн. = (7*14,26)/13,02 = 7,67; s2верхн. = 4*14,26/0,75 = 133,1.
7,67≤ Ợ2≤ 133,1
1.11, а) Оценить на уровне a=0,05 значимость уравнения регрессии Y по Х по критерию Фишера.
Решение. Вычислим суммы квадратов.
Общая сумма:
Q=å(yi- 
)2=226,86(см. табл. 4).
Регрессионная сумма:
QR=å( i- )2=155,95(см. табл. 4).
Остаточная сумма: Qe=å( i-у)2=71,29 (см. табл. 4).
Значение статистики Фишера:
F = 155,95/14,26 = 10,94
Уравнение регрессии значимо, если F > Fa,k1,k2, где степени свободы k1=m-1=2-1=1, k2=n-m=7-2=5. По табл. П4 находим критическое значение F0,05;1;5=6,61. Так как 10,94 > 6,61, то уравнение значимо: коэффициент регрессии b1 =2,36 значимо отличается от нуля.
1.11, б) Оценить на уровне a=0,05 значимость уравнения регрессии Y по Х по критерию Стьюдента.
Решение. Уравнение парной регрессии значимо, если
t = (2,36/3,78) 
= 3,30.
По табл. П2 находим t0,95;7-2=5=2,57. Так как 3,30 > 2,57, то гипотезу Но(Но : β1=0) отвергаем и принимаем противоположную гипотезу Н1: уравнение значимо.
1.12. Определить коэффициент детерминации R2 и раскрыть его смысл: на сколько процентов в среднем объем продаж зависит от размера торговой площади.
Решение. Используем формулу: R2= QR/Q = 155,95 / 226,86 = 0,7. R2 показывает, какая доля вариации зависимой переменной обусловлена вариацией объясняющей переменной. Ответ: эта доля составляет 70%.