Для непрерывных случайных величин наряду с законом распределения вероятностей рассматривают плотность вероятностей, которую обозначают так 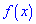 .
.
Плотностью вероятностей случайной величины 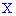 называют первую производную от интегральной функции распределения вероятностей
называют первую производную от интегральной функции распределения вероятностей 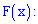
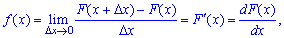
откуда дифференциал 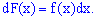
Поскольку прирост определяют зависимости
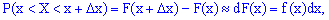
куплена плотности вероятностей на прирост случайной величины 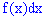 соответствует вероятность того, что случайная величина
соответствует вероятность того, что случайная величина 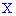 содержаться в промежутке
содержаться в промежутке 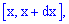 где
где 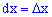 .
.
Геометрически на графике плотности вероятностей 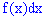 соответствует площадь прямоугольника с основанием
соответствует площадь прямоугольника с основанием 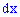 и высотой
и высотой 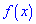
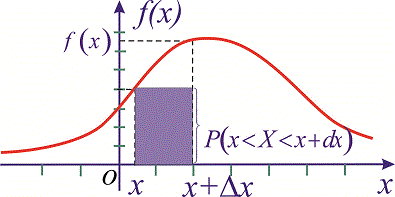
Свойства плотности вероятностей
1. Плотность вероятностей принимает положительные значения 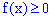 . Это свойство следует из определения первой производной от функции распределения
. Это свойство следует из определения первой производной от функции распределения 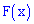 , которая в свою очередь является неубывающей функцией.
, которая в свою очередь является неубывающей функцией.
2. Условие нормирования случайной величины 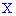
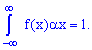
3.Вероятность попадания случайной величины в промежуток 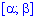 определяется зависимостью
определяется зависимостью
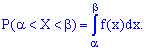
4. Функция распределения вероятностей непрерывной случайной величины определяется через плотность распределения вероятностей интегрированием
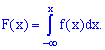
---------------------------------------
Рассмотрим задачи для закрепления материала на практике.
Пример 1. Закон распределения случайной величины 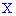 заданы функцией
заданы функцией
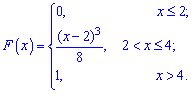
Найти плотность распределения вероятностей 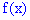 и построить графики обеих функций
и построить графики обеих функций 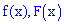 . Вычислить вероятность того, что случайная величина принадлежит промежутку
. Вычислить вероятность того, что случайная величина принадлежит промежутку 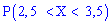
1.3. Генеральная совокупность и выборка
В математической статистике выделяют два фундаментальных понятия: генеральная совокупность и выборка.
Совокупностью - называется практически счетное множество некоторых объектов или элементов, интересующих исследователя;
Свойством совокупности называется реальное или воображаемое качество, присущее некоторым всем ее элементам.
Свойство может быть случайным или неслучайным.
Параметром совокупности называется свойство, которое можно квантифицировать в виде константы или переменной величины.
Простая совокупность характеризуется:
отдельным свойством (например: все студенты России);
отдельным параметром в виде константы или переменной (Все студенты женского пола);
системой непересекающихся (несовместных) свойств, к примеру: Все учителя и ученики школ г. Владивостока.
Сложная совокупность характеризуется:
системой, хотя бы частично пересекающихся свойств (Студенты психологического и математических факультетов ДВГУ, окончивших школу с золотой медалью);
системой параметров независимых и зависимых в совокупности; при комплексном исследовании личности.
Гомогенной или однородной называется совокупность, все характеристики которой присущи каждому ее элементу;
Гетерогенной или неоднородной называется совокупность, характеристики которой сосредоточены в отдельных подмножествах элементов.
Важным параметром является объем совокупности - количество образующих ее элементов. Величина объема зависит от того, как определена сама совокупность, и какие вопросы нас конкретно интересуют. Допустим нас интересует эмоциональное состояние студента 1-го курса в период сдачи конкретного экзамена в сессию. Тогда генеральная совокупность исчерпывается в течении получаса. Если нас интересует эмоциональное состояние всех студентов 1-го курса, то совокупность будет гораздо больше, и еще больше, если взять эмоциональное состояние всех студентов 1-го курса данного вуза и т.д.
Понятно, что совокупности большого объема можно исследовать только выборочным путем.
Выборкой называется некоторая часть генеральной совокупности, то, что непосредственно изучается.
Выборки классифицируются по репрезентативности, объему, способу отбора и схеме испытаний.
Репрезентативная - выборка адекватно отображающая генеральную совокупность в качественном и количественном отношениях. Выборка должна адекватно отображать генеральную совокупность, иначе результаты не совпадут с целями исследования.
Репрезентативность зависит от объема, чем больше объем, тем выборка репрезентативней. По способу отбора.
Случайная - если элементы отбираются случайным образом. Так как большинство методов математической статистики основывается на понятии случайной выборки, то естественно выборка должна быть случайной.
Неслучайная выборка:
механический отбор, когда вся совокупность делится на столько частей, сколько единиц планируется в выборке и затем из каждой части отбирается один элемент;
типический отбор - совокупность делится на гомогенные части, и из каждой осуществляется случайная выборка;
серийный отбор - совокупность делят на большое число разновеликих серий, затем делают выборку одной какой-либо серии;
комбинированный отбор - сочетаются рассматриваемые виды отбора, на разных этапах.
По схеме испытаний - выборки могут быть независимые и зависимые. По объему выборки делят на малые и большие. К малым относят выборки, в которых число элементов n < 30. Понятие большой выборки не определено, но большой считается выборка в которой число элементов > 200 и средняя выборка удовлетворяет условию 30< n< 200. Это деление условно.
Малые выборки используются при статистическом контроле известных свойств уже изученных совокупностей.
Большие выборки используются для установки неизвестных свойств и параметров совокупности.При планировании выборочного наблюдения с заранее заданным значением допустимой ошибки выборки необходимо правильно оценить требуемый объем выборки. Этот объем может быть определен на основе допустимой ошибки при выборочном наблюдении исходя из заданной вероятности 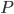 , гарантирующей допустимую величину уровня ошибки (с учетом способа организации наблюдения). Формулы для определения необходимой численности выборки n легко получить непосредственно из формул предельной ошибки выборки. Так, из выражения для предельной ошибки:
, гарантирующей допустимую величину уровня ошибки (с учетом способа организации наблюдения). Формулы для определения необходимой численности выборки n легко получить непосредственно из формул предельной ошибки выборки. Так, из выражения для предельной ошибки:
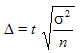
непосредственно определяется объем выборки n:

Эта формула показывает, что с уменьшением предельной ошибки выборки Δ существенно увеличивается требуемый объем выборки 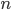 , который пропорционален дисперсии
, который пропорционален дисперсии 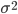 и квадрату критерия Стьюдента
и квадрату критерия Стьюдента 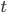 .
.
Для конкретного способа организации наблюдения требуемый объем выборки 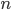 вычисляется согласно формулам, приведенным в табл. 9.4.
вычисляется согласно формулам, приведенным в табл. 9.4.
Репрезентативность выборки - иными словами, ее представительность - это способность выборки представлять изучаемые явления достаточно полно - с точки зрения их изменчивости в генеральной совокупности.
Конечно, полное представление об изучаемом явлении, во всем его диапазоне и нюансах изменчивости, может дать только генеральная совокупность. Поэтому репрезентативность всегда ограничена в той мере, в какой ограничена выборка. И именно репрезентативность выборки является основным критерием при определении границ генерализации выводов исследования. Тем не менее, существуют приемы, позволяющие получить достаточную для исследователя репрезентативность выборки.
Случайный отбор?
Первый и основной прием - это простой случайный отбор. Он предполагает обеспечение таких условий, чтобы каждый член генеральной совокупности имел равные с другими шансы попасть в выборку. Случайный отбор обеспечивает возможность попадания в выборку самых разных представителей генеральной совокупности. При этом принимаются специальные меры, исключающие появление какой-либо закономерности при отборе. И это позволяет надеяться на то, что в конечном итоге в выборке изучаемое свойство будет представлено если и не во всем, то в максимально возможном его многообразии.
Пример
_____________
Изучая агрессивность подростков, исследователь может случайным образом остановить с вой выбор на 3 классах разных школ и затем случайным образом отобрать по 10 учащихся из каждого класса. Если же исследователь просит испытуемого пригласить на обследование своих друзей, он грубо нарушает принцип случайности отбора.
_____________
Второй способ обеспечения репрезентативности - это стратифицированный случайный отбор, или отбор по свойствам генеральной совокупности. Он предполагает предварительное определение тех качеств, которые могут влиять на изменчивость изучаемого свойства (это может быть пол, уровень дохода или образования и т. д.). Затем определяется процентное соотношение численности различающихся по этих качествам групп (страт) в генеральной совокупности и обеспечивается идентичное процентное соотношение соответствующих групп в выборке. Далее в каждую подгруппу выборки испытуемые подбираются по принципу простого случайного отбора.
Вариационный ряд. Статистическое распределение выборки. Основные характеристики вариационного ряда.
Ряды, построенные по количественному признаку, называются вариационным.
Ряды распределений состоят из вариантов (значений признака) и частот (численности групп). Частоты, выраженные в виде относительных величин (долей, процентов) называются частостями. Сумма всех частот называется объёмом ряда распределения.
По виду ряды распределения делятся на дискретные (построены по прерывным значениям признака) и интервальные (построены на непрерывных значениях признака).
Вариационный ряд представляет собой две колонки (или строки); в одной из которых приводятся отдельные значения варьирующего признака, именуемые вариантами и обозначаемые Х; а в другой – абсолютные числа, показывающие сколько раз (как часто) встречается каждый вариант. Показатели второй колонки называются частотами и условно обозначают через f. Еще раз заметим, что во второй колонке могут использоваться и относительные показатели, характеризующие долю частоты отдельных вариантов в общей сумме частот. Эти относительные показатели именуются частостями и условно обозначают через ω Сумма всех частостей в этом случае равна единице. Однако частоты можно выражать и в процентах, и тогда сумма всех частостей дает 100%.
Если варианты вариационного ряда выражены в виде дискретных величин, то такой вариационный ряд именуют дискретным.
Для непрерывных признаков вариационные ряды строятся как интервальные, то есть значения признака в них выражаются «от… до …». При этом минимальны значения признака в таком интервале именуют нижней границей интервала, а максимальное – верхней границей.
Интервальные вариационные ряды строят и для дискретных признаков, варьирующих в большом диапазоне. Интервальные ряды могут быть с равными и неравными интервалами.
Рассмотрим как определяется величина равных интервалов. Введем следующие обозначения:
i – величина интервала;
- максимальное значение признака у единиц совокупности;
– минимальное значение признака у единиц совокупности;
n – число выделяемых групп.
, если n известно.
Если число выделяемых групп трудно заранее определить, то для расчета оптимальной величины интервала при достаточном объеме совокупности может быть рекомендована формула, предложенная Стерджессом в 1926 году:
n = 1+ 3.322 lg N, где N – число единиц в совокупности.
Величина неравных интервалов определяется в каждом отдельном случае с учетом особенностей объекта изучения.
Статистическим распределением выборки называют перечень вариант и соответствующих им частот (или относительных частот).
Статистическое распределение выборки можно задать в виде таблицы, в первой графе которой располагаются варианты, а во второй - соответствующие этим вариантам частоты ni, или относительные частоты Pi.
Статистическое распределение выборки
| Варианты хi | x1 | x2 | x3 | … | xi | … | xk |
| Число наблюдений (частота) ni | n1 | n2 | n3 | … | ni | … | nk |
| Относительная частота Pi | P1 | P2 | P3 | … | Pi | … | Pk |
Интервальными называются вариационные ряды, в которых значения признаков, положенных в основу их образования, выражены в определенных пределах (интервалах). Частоты в этом случае относятся, не к отдельным значениям признака, а ко всему интервалу.
Интервальные ряды распределения строятся по непрерывным количественным признакам, а также по дискретным признакам, варьирующим в значительных пределах.
Интервальный ряд можно представить статистическим распределением выборки с указанием интервалов и соответствующих им частот. При этом в качестве частоты интервала принимают сумму частот вариант, попавших в этот интервал.
При группировке по количественным непрерывным признакам важное значение имеет определение размера интервала.