Модой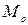 
называют варианту, которая имеет наибольшую частоту.
Например, для ряда
Медианой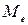 
называют варианту, которая делит вариационный ряд на две части, равные по числу вариант.
Размахом варьирования R называют разность между наибольшей и наименьшей вариантами: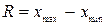 
.
Средним абсолютным отклонением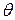 
называют среднее арифметическое абсолютных отклонений: 
.
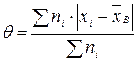Среднее абсолютное отклонение служит для характеристики рассеяния вариационного ряда.
Коэффициентом вариации V называют выраженное в процентах отношение выборочного среднего квадратического отклонения к выборочной средней: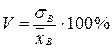 
Числовые значения, характеризующие генеральную совокупность, называются параметрами.
Статистическое оценивание может выполняться двумя способами:
1) точечная оценка – оценка, которая дается для некоторой определенной точки;
2) интервальная оценка – по данным выборки оценивается интервал, в котором лежит истинное значение с заданной вероятностью.
Точечная оценка – это оценка, которая определяется одним числом. И это число определяется по выборке.
Точечная оценка называется состоятельной, если при увеличении объема выборки выборочная характеристика стремится к соответствующей характеристике генеральной совокупности.
Точечная оценка называется эффективной, если она имеет наименьшую дисперсию выборочного распределения по сравнению с другими аналогичными оценками.
Точечную оценку называют несмещенной, если ее математическое ожидание равно оценивающему параметру при любом объеме выборки.
Несмещенной оценкой генеральной средней (математического ожидания) служит выборочная средняя в:
в=ini,
где xi – варианты выборки; ni – частота встречаемости вариант xi; n – объем выборки.
Интервальная оценка – это числовой интервал, который определяется двумя числами – границами интервала, содержащий неизвестный параметр генеральной совокупности.
Доверительный интервал – это интервал, в котором с той или иной заранее заданной вероятностью находится неизвестный параметр генеральной совокупности.
Доверительная вероятность p – это такая вероятность, что событие вероятности (1-р) можно считать невозможным. α=1-р – это уровень значимости. Обычно в качестве доверительных вероятностей используют вероятности, близкие к 1. Тогда событие, что интервал накроет характеристику, будет практически достоверным. Это р≥0,95, р≥0,99, р≥0,999.
Для выборки малого объема (n<30) нормально распределенного количественного признака х доверительный интервал может иметь вид:
в-mt≤≤в+mt (р≥0,95),
где – генеральное среднее; в – выборочное среднее; t – нормированный показатель распределения Стьюдента с(n-1) степенями свободы, который определяется вероятностью попадания генерального параметра в данный интервал; m – ошибка выборочной средней.
Сравнение двух средних произвольно распределенных генеральных совокупностей (большие независимые выборки)
В предыдущем параграфе предполагалось, что генеральные совокупности Х и Y распределены нормально, а их дисперсии известны. При этих предположениях в случае справедливости нулевой гипотезы о равенстве средних и независимых выборках критерий Z распределен точно нормально с параметрами 0 и 1.
Если хотя бы одно из приведенных требований не выполняется, метод сравнения средних, описанный в § 10, неприменим.
Однако если независимые выборки имеют большой объем (не менее 30 каждая), то выборочные средние распределены приближенно нормально, а выборочные дисперсии являются достаточно хорошими оценками генеральных дисперсий и в этом смысле их можно считать известными приближенно. В итоге критерий
.
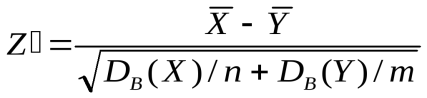распределен приближенно нормально с параметрами М(Z')==0 (при условии справедливости нулевой гипотезы) и σ(Z')=1 (если выборки независимы).
Итак, если: 1) генеральные совокупности распределены нормально, а дисперсии их неизвестны; 2) генеральные совокупности не распределены нормально и дисперсии их неизвестны, причем выборки имеют большой объем и независимы, — можно сравнивать средние так, как описано в § 10, заменив точный критерий Z приближенным критерием Z'. В этом случае наблюдаемое значение приближенного критерия таково:
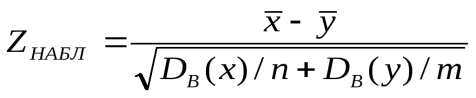
Замечание. Поскольку рассматриваемый критерий—приближенный, к выводам, полученным по этому критерию, следует относиться осторожно.
Пример. По двум независимым выборкам, объемы которых соответственно равны n=100 и m==120, найдены выборочные средние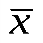 
=32,4, 
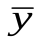==30,1 и выборочные дисперсии Dв(Х)= 15,0, Dв(Y)=25,2. При уровне значимости 0,05 проверить нулевую гипотезу Н0: М (X) = М (Y), при конкурирующей гипотезе Н1: М (X) > М (Y).
Решение. Подставив данные задачи в формулу для вычисления наблюдаемого значения приближенного критерия, получим
Z’набл = 3,83.
По условию, конкурирующая гипотеза имеет вид М (X) > М (Y), поэтому критическая область — правосторонняя.
Найдем критическую точку по равенству
Ф (zкр) = (1-2α)/2 = (1—2·0,05)/2= 0,45.
По таблице функции Лапласа находим zкр = 1,64.
Так как Zнабл >zкр — нулевую гипотезу отвергаем. Другими словами, выборочные средние различаются значимо.