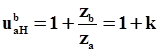Общая последовательность построения картины скоростей.

Сначала строим треугольник скоростей для входа, затем для сателлита или блока сателлитов и последним для выхода. Вот последовательность: вход, сателлиты, выход.

Когда строим картину скоростей для сателлита всегда ищем две точки: общую со стойкой, скорость которой равна нулю и общую с входом.

В нашем случае входным звеном является солнце, проводим линию, относящуюся к солнце под любым углом. Далее строим сателлит. Точка А будет общая точка сателлита с нулем, со стойкой, нулевым звеном. Скорость этой точки равна нулю, сносим ее на вертикальную ось. Точка В будет общая у сателлита со входом. Сносим ее на линию солнца. У сателлита известны две точки, через них проводим линию, являющуюся картиной скоростей для сателлита, это вторая линия. Наконец последняя линия для выходного звена, то есть для водила. Выходное звено всегда центральное, поэтому скорость его на оси равна нулю. Вторая точка с известной уже скоростью это точка на водиле общая с сателлитом. Это точка D. Сносим ее на линию сателлита. В результате построили три линии, которые образуют картину скоростей для планетарного ряда..

 

По картине скоростей расставим направление вращение звеньев. Вход и выход, солнце и водило вращаются в одну сторону. Сателлиты в другую, так как наклон эпюры скоростей сателлитов будет другой чем у солнца и водила. Это можно показать с помощью векторов оборотов n_a, n_H,n_c, а также с помощью круглых стрелок угловых скоростей w_c, w_H, w_a

С помощью картины скоростей, если по всем осям выдержан масштаб, можно определить любые передаточные отношения. Например, передаточное отношение от солнца к водилу при заторможенном эпицикле. Отрезки mt и mn можно взять на отрезке прямой, проведенной на любом радиусе.

 

 

 

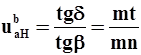КИНЕМАТИКА ПЛАНЕТАРНЫХ ПЕРЕДАЧ.

 

Вывод общего уравнения кинематики планетаных передач.

Покажем универсальный способ определения различных передаточных отношений в планетарной передаче с помощью всего лишь одного уравнения- общего уравнения кинематики планетарной передачи. Для вывода этого уравнения воспользуемся методом инверсии или методом остановленного водила, методом Виллиса.

В планетарной передаче конструктора могут интересовать различные передаточные отношения. Напрмер при заторможенном эпицикле u_aH^b, u_cH^b, u_Ha^b,

При заторможенном солнечном колесе u_bH^a, u_cH^a, u_Hb^a и другие.

Самые простые передаточные отношения с точки зрения простоты их получения через числа зубьев, являются передаточные отношения при заторможенном водиле Н. При заторможенном водиле любой планетарный механизм превращается в паразитный или ступенчатый ряд. Как записать такие передаточные отношения через числа зубьев мы уже знаем. Например для нашего планетарного ряда

 

 

 

 

Оказывается,что все другие передаточные отношения легко выражаются через эти, для этого выведем основное уравнение кинематики.

 

Для этого рассмотрим два движения. Первое основное движение. когда заторможенным является например эпицикл. Второе рассматриваемое движение это обращенное движение, когда всему механизму сообщается движение с угловой скоростью равной ω _H но в противоположную сторону. При этом водило окажется неподвижным, при этом угловые скорости всех звеньев изменяться на величину -ω _H.

 

 

 

 

Основное движение Обращенное движение

 

 

Угловые скорости в основном и обращенном движении

 

 

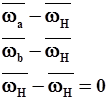Основное движение Обращенное движение

 

 

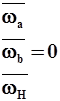Это два равноправных движения, в каждом из них можем записывать передаточные отношения.

Запишем в обращенном движении передаточное отношение от солнца к эпициклу и немного преобразуем его

 

 

 

 

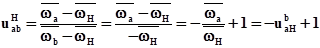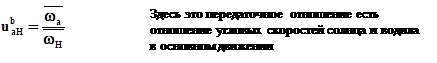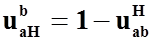Итак получаем общее уравнение кинематики

 

Либо в общем виде

 

 

Это уравнение необходимо запомнить Оно читается как: передаточное отношение от какого-то звена m к водилу H при остановленном звене n равно единице минус передаточное отношение от m к n при остановленном H, при это во втором передаточном отношении надо просто поменять индексы местами по диагонали.

 

Рассмотрим различные примеры использования общего уравнения кинематики при определении передаточных отношений различных схем планетарных передач.

 

 

РЯД ДЖЕМСА.

Этот ряд называют еще простой планетарный ряд, эпициклический ряд, ряд авН

Набольшее распространение этот ряд имеет в качестве силовой передачи, редуктора, при заторможенном эпицикле.

 

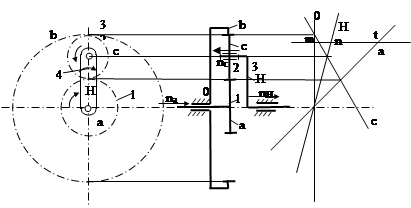Строим картину скоростей. Вход –солнце, под любым углом. Сателлит- две точки: с нулём и со входом. Выход – водило: ноль на оси и общая точка с сателлитом. Расставляем в соответствии с картиной и наклом эпюр скоростей вектора оборотов звеньев и круглые стрелки угловых скоростей.

 

 

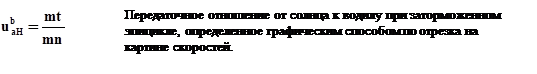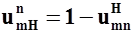Найдем различные передаточные отношения аналитическим методом с помощью общего уравнения кинематики

 

От солнца к водилу, при этом меняем индексы по диагонали и для написания передаточного отношения от солнца к эпициклу при заторможенном водиле смотрим на схему. Имеем паразитный ряд у которого одно внешнее зацепление, поэтому знак минус

 

От сателлита к водилу

 

Рассмотрим пример z_a=12, z_b=60, z_c=24, число оборотов солнца, звена на входе равно

n_a= 1000 об\.мин

 

Передаточные отношения нужны, чтобы определять частоту вращения звеньев и направление вращения

 

u_aH^b=n_a/n_H=1-z_b/z_a=1+60/12=6 откуда n_H=n_a/ u_aH^b=1000/6=166,7 об\мин

 

Обороты водила в 6 раз медленнее оборотов солнца и направлены в ту же строну.

Найдем обороты сателлита из передаточного отношения u_cH^b

 

u_cH^b=n_c/n_H=1-z_b/z_c=1- 60/24=-1,5 откуда n_c=n_H* u_cH^b=166,7*1,5=250,05 об\мин

 

Здесь знак в оборотах, при подстановке передаточного отношения, опущен; мы ищем модуль оборотов.

Знание всех оборотов позволяет найти важное для конструктора число: относительные обороты сателлита относительно водила. По относительным оборотам рассчитываются подшипники качения, на которыx сидит сателлит на оси водила.

	__ __ __ nс(Н)= nc- nH

 

 

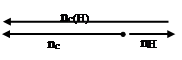n_с(Н)= n_c + n_H=250,05+166,7=416,75 об\мин

 

На эти обороты и необходимо рассчитывать подшипники качения.

 

Общее замечание состоит в том, что если вектора абсолютных скоростей сателлитов и водила направлены в разные стороны, то при подсчете относительных оборотов модули векторов складываются, если в одну, то вычитаются. В

В нашем варианте в разные, поэтому складываются.

 

Часто отношение чисел зубьев z_b/z_a равное |u_ab^H| обозначают через к и называют характеристикой планетарного ряда.

		Характеристика планетарного ряда

 

 

Передаточное отношение от солнца к водилу через характеристику планетарного ряда запишется как

 

 

Характеристика планетарного ряда характеризует габариты планетарной передачи. С ростом к, с ростом передаточного отношения, растет радиус эпицикла и габариты передачи. Отсюда ограничение на конструктивно целесообразное максимальное передаточное отношение равное 8 в таком ряду.

Минимальное передаточное отношение также ограничено, оно около 3. При уменьшении к сближаются значения радиусов r_b и r_a и не остается места сателлитам. Итак диапазон передаточных отношений и КПД равны.

 

u_aН^в= 2,7….8 при этом КПД h= 0,98…0,97

 

 

Следующая схема это модифицированный рад ДЖЕМСА. В этой схеме сателлит заменен блоком сателлитов.

 

МОДИФИЦИРОВАННЫЙ РЯД ДЖЕМСА или эпициклический ряд с внешним и внутренним зацеплением.

 

 

 

 

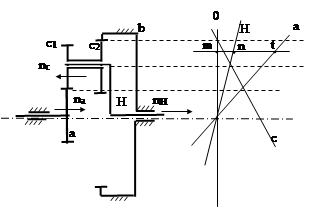Строим картину скоростей. Вход –солнце, под любым углом. Сателлит- две точки: с нулём и со входом. Выход – водило: ноль на оси и общая точка с сателлитом. Расставляем в соответствии с картиной и наклом эпюр скоростей вектора оборотов звеньев.

 

 

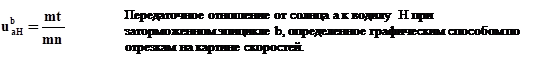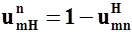Найдем различные передаточные отношения аналитическим методом с помощью общего уравнения кинематики

 

От солнца к водилу, при этом меняем индексы по диагонали и для написания передаточного отношения от солнца к эпициклу при заторможенном водиле смотрим на схему. Имеем ступенчатый ряд у котрого одно внешнее зацепление и одно внутреннее, поэтому знак минус Движение передаем в ряду от а к с₁ и от с₂ к b.

 

 

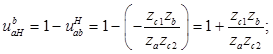
От сателлита к водилу

 

 

За счет блока сателлитов расширяется диапазон допустимых передаточных отношений

 

u_aH^b= 2…15 КПД высок h= 0,98…0,97

 

РЕДУКТРОР ДАВИДА С ДВУМЯ ВНУТРЕННИМИ ЗАЦЕПЛЕНИЯМИ

 

 

 

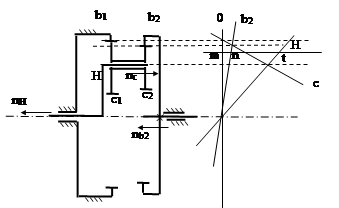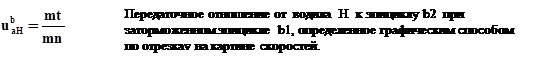Строим картину скоростей. Вход –водило, под любым углом. Сателлит- две точки: с нулём и со входом. Выход – эптцикл: ноль на оси и общая точка с сателлитом. Расставляем в соответствии с картиной и наклоном эпюр скоростей вектора оборотов звеньев.

 

 

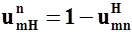Найдем различные передаточные отношения аналитическим методом с помощью общего уравнения кинематики

 

В этой схеме, чтобы получить редуктор ведущим должно быть водило, ведомым эпицикл. В этом передаточном отношении неправильное расположение нижних индексов. Чтобы воспользоваться общим уравнением кинематики надо поменять нижние индексы. Для этого делим единицу на u_b2H^b1. И дальше общее уравнение кинематики.

 

 

 

 

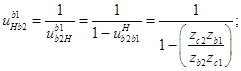Передаточное отношение от сателлита к водиу.

 

 

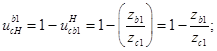В этой схеме диапазон допустимых передаточных отношений и КПД

 

u_Hb2^b1 = 30 … 1000 КПД η = 0,9 ….0,1

Эта схема используется, в основном, в качестве кинематических передач.

 

u
h	0,9	0,75	0,6	0,45	0,25	0,12

 

РЕДУКТОР ДАВИДА С ДВУМЯ ВНЕШНИМИ ЗАЦЕПЛЕНИЯМИ

 

 

 

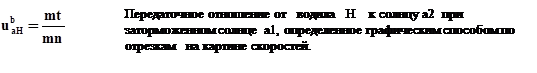Строим картину скоростей. Вход –водило, под любым углом. Сателлит- две точки: с нулём и со входом. Выход – солнечное колесо а2: ноль на оси и общая точка с сателлитом. Расставляем в соответствии с картиной и наклоном эпюр скоростей вектора оборотов звеньев.

 

В этой схеме, чтобы получить редуктор, ведущим должно быть водило, ведомым солнце. В этом передаточном отношении неправильное расположение нижних индексов. Чтобы воспользоваться общим уравнением кинематики надо поменять нижние индексы. Для этого делим единицу на u_а2H^а1. И дальше общее уравнение кинематики.

 

Передаточное отношение от сателлита к водиу.

 

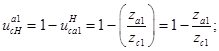В этой схеме диапазон допустимых передаточных отношений

 

u_Hа2^а1 = 2 … 300

КПД значительно ниже чем в предыдущей схеме, так как здесь два внешних зацепления.

Эта схема используется, в основном, в качестве кинематических передач.

 

ПЛАНЕТАРНАЯ ПЕРЕДАЧА СО СВОБОДНЫМ ВОДИЛОМ

 

 

Планетарная ступень со свободным водилом на самом деле представляет собой две последовательно соединенные ступени. Размеры звеньев таковы, что эти две ступени можно слить в одну и значительно уменьшить осевые габариты Свободное водило обозначает то что водило не является ни входным ни выходным звеном. Оно внутри, поддерживает сателлиты.

 

РАСШИФРОВКА СХЕМЫИ КАРТИНА СКОРОСТЕЙ

 

 

 

 

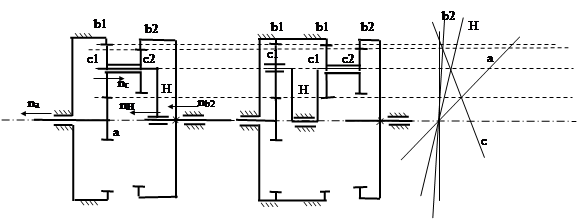
На этом рисунке показано как расшифровывается схема со свободным водилом. В первой ступени движение передается от входа, солнца к водилу. Во второй ступени об водила к выходу, которым в данной схеме является эпицикл b2. Сателлиты с1 и заторможенные эпициклы b1 одинаковы в обеих схемах. Если бы они были разными, это бы были чисто две планетарные ступени, соединённые последовательно. В нашем же случае, когда они одинаковы мы можем эти две ступени соединить в одну, при этом водило становится внутренним звеном, как бы свободным, не являющимся ни входным ни выходным.

Передаточное отношение в схеме со свободным водилом записывается также как и расшифровка то есть от входа к водилу и от водила к выходу при одном и том же заторможенном звене

 

 

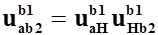
Выразим через числа зубьев., первая ступень планетарный ряд Джемса, вторая ступень редуктор Давида с двумя внутренними зацеплениями.

 

 

 

Эта схема может использоваться и в качестве силовой, так как довольно высок КПД и в качестве кинематической, так как возможно большое передаточное отношение в одной ступени.

 

 

u
h	0,95	0,9	0,85	0,75	0,6	0,35

 

Приведем итоговую таблицу по планетарным передачам

 

 

 

 

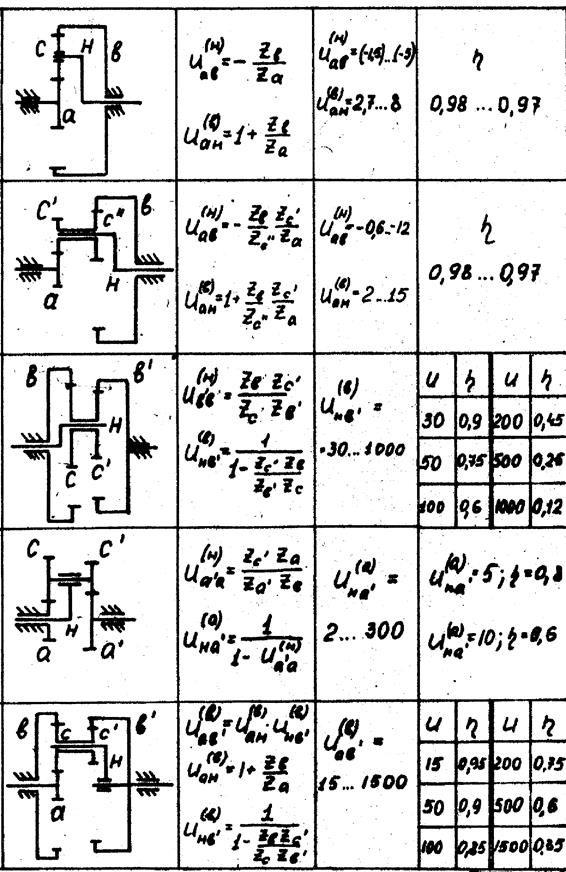
Рассмотрим несколько примеров кинематического анализа зубчатых передач.

 

 

Последовательность анализа состоит из нескольких пунктов.

 

 

1. Проанализировать схему зубчатого механизма, определив сколько ступеней соединены последовательно от входа к выходу, как называются эти ступени с неподвижными звеньями и планетарные, от какого к какому звену в ступени передается движение.

2.

3. Проверить правильность задания чисел зубьев через условие соосности в разных ступнях. Если необходимо, определить неизвестное число зубьев.

4. Вычертить кинематическую схему зубчатой передачи в масштабе и отметить на ней выходное и выходное звено с указанием направления вращения на входе. Модуль всех зубчатых колес принять равным m=1 мм.

5. Обозначить арабскими цифрами звенья передачи, при этом нужно отбросить, если они есть, параллельные ветви. Подсчитать степень подвижности механизма.

6. Построить картину скоростей для планетарных ступеней и определить и обозначить с помощью этой картины направление вращения звеньев планетарной ступени. Обозначить направление вращения и других звеньев.

7. По картине скоростей определить передаточное планетарной ступени, как отношение соответствующих отрезков.

8. Записать общее передаточное отношение зубчатого механизма, как произведение передаточного отношения ступеней.

9. Выразить через числа зубьев и, подставив значения чисел зубьев, численно подсчитать каждое передаточное отношение. Сравнить полученные значения передаточных отношения для планетарных ступеней со значениями, полученными с помощью картины скоростей.

10. Подсчитать численное значение общего передаточного отношения. Определить частоту вращения выходного звена.

11. Для планетарного механизма найти передаточное отношение от сателлита к водилу.

12. Зная частоту вращения входного звена, найти частоту вращения всех звеньев зубчатого механизма. Для сателлита, кроме того, найти относительные обороты сателлита относительно водила. При этом проверить по знаку передаточного правильность направления вращения, найденного по картине скоростей.

 

 

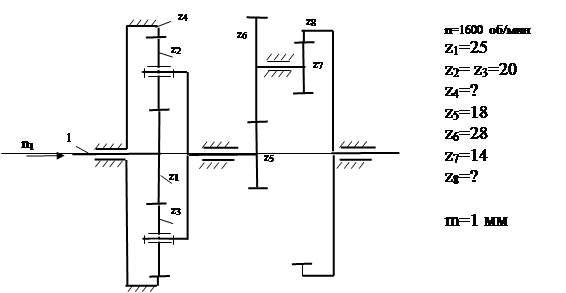
Пример 1

 

 

Решение

1. Кинематическая схема зубчатого механизма состоит из трех ступеней. Первая ступень - планетарная, простой планетарный ряд Джемса, движение передается от солнца z₁ к водилу H. Вторая ступень - цилиндрическая зубчатая передача внешнего зацепления, движение передается от шестерни z₅ к z₆. Третья ступень - цилиндрическая передача внутреннего зацепления, движение передается от шестерни z₇ к зубчатому колесу с внутренними зубьями z₈. Зубчатое колесо z₈ является выходным звеном всего зубчатого механизма.

2. Можно записать два условия соосности: для планетарной ступени и для двух ступеней с неподвижными осями.

 

z₄ - z₂= z₁ + z_2; ? - 20 = 25 + 20; z₄= 65 -

z₅+ z₆= z₈- z₇ ; 18 + 28 =? - 14; z₈=60

 

 

 

 

 

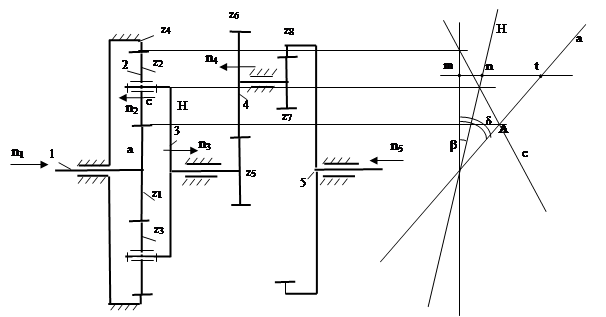Число звеньев, число кинематических пар

 

n=5; P₅=5; P₄=4 W= 3n – 2*P5 - P₄= 3*5 - 2*5 – 4 = 1

 

Передаточное отношение планетарного ряда с помощью картины скоростей

 

u_z1H^z4=tgδ /tgβ = mt/mn=22/6=3,66

 

Общее передаточное отношение

 

u₁₅=u₁₃u₃₄u₄₅= u_z1H^z4 u₃₄u₄₅=3,6*1,55*4,29=23,94

 

 

Передаточное отношение планетарной ступени

 

u_{13 =}u_z1H^z4=1- u_z1z4^H=1-(-z4/z1)=1+z4/z1=1+65/25=3,6

 

Передаточное отношение цилиндрической зубчатой передачи внешнего зацепления

 

u₃₄=z6/z5=28/18=1,55

 

Передаточное отношение цилиндрической зубчатой передачи внутреннего зацепления

 

u₄₅=z8/z7=60/14=4,29

 

 

Частота вращения выходного вала

 

n₅=n₁/ u₁₅=1600/23,94=66,83 [об/мин]

 

n₃= n_H =n₁/ u₁₃=1600 / 3,6=444,44 [об/мин]

 

n₄=n₁/ (u₁₃ u₃₄)=1600/(3,6*1,55)=286,73 [об/мин]

 

Передаточное отношение от сателлита к водилу, воспользуемся общим уравнением кинематики

 

u_СH^z4=1- u_Сz4^H=1-(z4/z2)=1-65/20=-2,25

Обороты сателлита определим как

n_c/n_H= u_СH^z4 n_c= u_СH^z4 n_H=2,25*444,44= 999,999 [об/мин]

 

Относительные обороты сателлита относительно водила

___ __ __

n_cН= n_c- n_Н., в нашем случае угловые скорости сателлита и водила направлены в разные стороны.

Следовательно при определении модуля угловой скорости сателлита в относительном движении относительно водила модули абсолютных скоростей необходимо складывать.

 

n_cН= n_c+ n_Н = 999,999 + 444,444 = 1445 [об/мин]

Оценка работоспособности подшипников качения сателлитов будет производится именно по этим оборотам

 

 

Пример 2

 

Решение

 

 

 

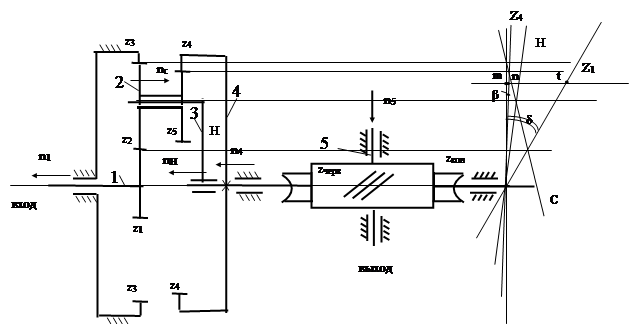
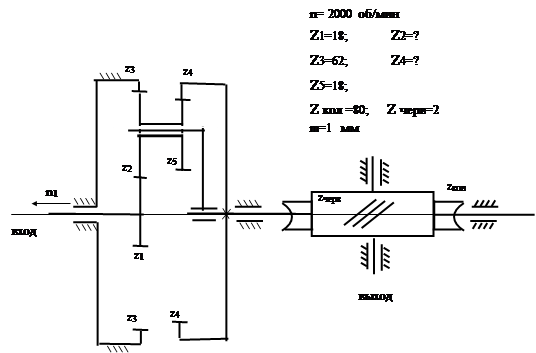
1. Кинематическая схема зубчатого механизма состоит из двух ступеней. Первая ступень планетарный ряд со свободным водилом; движение передается от солнца z₁ эпициклу Z₄. Вторая ступень – червячная передача. Червячное зубчатое колесо z_кол является выходным звеном всего зубчатого механизма.

 

2. Можно записать два условия соосности для планетарной ступени.

 

z₃ - z₂= z₁ + z_2; 62 -? = 18 +?; Z₂ = 22

z₁+ z₂= z₄- z₅ ; 18 + 22 =? - 18; z₄=58