Приложения 16
Лабораторная работа № 28
Расчет числовых характеристик случайной величины из опыта
Цель работы:
1. Изучить основы методов обработки результатов наблюдения.
2. Ознакомиться с методикой расчета числовых характеристик случайной величины.
3. Научиться применять пакет прикладных программ ЕХСЕL при обработке результатов наблюдения.
Задание
По исходным данным:
1. Постройте статистический ряд распределения организаций по указанному для каждого варианта признаку.
2. Рассчитайте числовые характеристики дискретного ряда распределения.
3. Постройте интервальный ряд распределения и рассчитайте для него числовые характеристики: выборочное среднее, среднее квадратическое отклонение, коэффициент вариации.
4. Для полученного ряда распределения постройте графики: полигон и кумулятивную кривую. Графически определите значение моды и медианы.
5. Постройте гистограмму и графически определите значение моды.
6. Сравните выборочное среднее для дискретного и интервального рядов между собой. Объясните причину расхождения.
Сделайте выводы по результатам выполнения задания.
1. ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
1.1. Вариационные ряды
Пусть в результате какого-либо статистического наблюдения конкретного явления получены числовые данные, характеризующие его (для изучения случайной величины X извлечена выборка объема n):
x1,x2,...,xn (2.1)
Значения x i называют вариантами, m i - число, показывающее, сколько раз встречается вариант x i, называют частотой варианта (mi). Проведя ранжирование вариантов (обычно располагают в порядке возрастания) и указав относительно каждого варианта его частоту, получают статистическое распределение выборки или вариационный ряд. Различают дискретные и интервальные вариационные ряды.
Пример 1. При взвешивании 50 одинаковых деталей, изготовленных на одном станке, были получены численные значения веса их в граммах.
Вариационный ряд для веса данной детали представлен в табл. 2.1.
Таблица 2.1.
Дискретный вариационный ряд
| xi | |||||
| mi |
Для построения интервального ряда необходимо определить величину интервала, установить полную шкалу интервалов, в соответствии с ней сгруппировать результаты наблюдений. Для определения оптимальной величины интервала h, при которой ряд не был бы слишком громоздким и, в тоже время, позволил бы выявить характерные черты случайной величины X, используют формулу Стэрджеса
 (2.2)
(2.2)
где x min и x max - максимальная и минимальная варианты.
За начало первого интервала рекомендуется принимать величину, равную a1 = (x min - h/2), тогда
 , где i = 2,3,... (2.3)
, где i = 2,3,... (2.3)
Построение интервалов продолжают до тех пор, пока начало следующего по порядку интервала не будет равным или большим xmax.
Пример 2. Производится замер диаметра (в мм) шейки плунжера после шлифования. Всего исследовалось n = 200 деталей, причем x max = 6.83, x min = 6.68.
Величина интервала
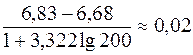
a1 = 6.68 - 0.01 = 6.67,
a2 = 6.67 + 0.02 = 6.69,
...
a9 = 6.83.
Для каждого интервала подсчитывается количество вариант, попавших в данный интервал, причем в интервал включаются варианты больше нижней границы и меньше или равные верхней границы интервала.
Таблица 2.2.