Коэффициент вариации по среднему квадратичному отклонению -

(2.12)

Размах вариации - R

R = max. X_i - min X_i (2.13)

Асимметрия - As

(2.14)

или

(2.15)

Эксцесс - Ex

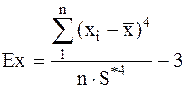(2.16)

или

(2.17)

Средние величины являются обобщающими количественными характеристиками совокупности однотипных явлений по варьирующему признаку. Среднее арифметическое характеризует среднее значение, около которого группируются возможные значения случайной величины, а дисперсия есть мера разбросанности этих значений относительно среднего. Среднее квадратичное отклонение, так же как и дисперсия, является мерой колеблемости, но в отличие от дисперсии представляет собой абсолютную величину, выраженную в тех же единицах, что и варианты. Коэффициент вариации является относительным показателем колеблемости. Вариационный размах (или широта распределения) неустойчивая, чрезвычайно зависящая от случайностей величина, служащая для приблизительной оценки вариации.

Асимметрия и эксцесс являются показателями отклонения функции распределения f(x) для X от нормального закона распределения.

Если As = 0, то кривая для f(x) симметрична, при As ¹ 0 - асимметрична. Эксцесс характеризует крутизну кривой распределения.

Если Ex ¹ 0, то вершина кривой для f(x) находится либо выше (при Ex > 0), либо ниже (при Ex < 0) вершины кривой нормального распределения.

1.3. Интервальные оценки параметров распределения

В п.1.2. были рассмотрены точечные оценки некоторых характеристик распределения случайной величины X через характеристики выборки. Поэтому точечные оценки сами являются случайными величинами, законы которых зависят от закона распределения X и объема выборки n [2]. Чтобы дать представление о точности и надежности точечных оценок используют так называемые доверительные интервалы и доверительные вероятности.

Доверительным интервалом для некоторой характеристики Q называют такой интервал (e₁,e₂), который с заранее выбранной вероятностью Ã содержит истинное значение параметра Q, т.е.

P (e₁ < Q < e₂) = Ã. (2.18)

Здесь Ã называют доверительной вероятностью. Обычно значение Ã выбирают близкое к единице: 0,9; 0,95; 0,99; 0,999. a = 1 - Ã называют уровнем значимости.

1.3.1. Построение доверительного интервала для математического ожидания

Если случайная величина X подчиняется нормальному закону распределения, то доверительный интервал для истинного значения x измеряемой величины может быть построен следующим образом.

Первый способ. Доверительная оценка при известной точности измерений.

Если заранее известно среднее квадратичное отклонение (или другая связанная с ней характеристика точности измерений), то доверительный интервал имеет вид

(2.19)

где n - объем выборки, `x - среднее арифметическое, t(Ã) определяется по заданной доверительной вероятности из условия [1,2]:

2 Ф(t) = Ã (2.20)

Здесь Ф(t) = - функция Лапласа, значения которой представлены в таблице приложения 1.

Второй способ. Доверительная оценка при неизвестной точности измерений.

Если среднее квадратичное отклонение s заранее неизвестно, то вместо него используют эмпирическое отклонение. Известно [2], что статистика

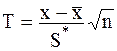(2.21)

подчиняется закону Стьюдента с f = n - 1 степенями свободы. Исходя из этого, доверительный интервал в данном случае имеет вид [1,2]

(2.22)

где t (Ã, n - 1) зависит и от объема выборки. t (Ã, n - 1) определяется из таблицы приложения 2.

1.3.2.Построение доверительного интервала для дисперсии и среднего квадратичного отклонения.

Известно [2], что статистика

(2.23)

подчиняется закону распределения Пирсона или «c - распределению » с f = n - 1 степенями свободы. Исходя из этого, доверительный интервал для дисперсии s² случайной величины имеет вид [1,2]

(2.24)

где c₁² и c₂² - значения, определяемые из таблиц для распределения Пирсона ([3], приложение 5) соответственно для вероятностей Ã₁ = (1 - Ã) / 2 и Ã₂ = = (1 + Ã) / 2 и числа степеней свободы f = n - 1.

Пусть , тогда (2.24) примет вид

g₁² × S^*2 < s² < g₂² × S^*2, (2.25)

где значения g² протабулированы для n и Ã (приложение 4).

Для интервальной оценки среднего квадратичного отклонения служит неравенство

g₁ × S^* < s < g₂ × S^*. (2.26)

2. ИСПОЛЬЗОВАНИЕ ЭВМ

2.1. Использование программного продукта MATHCAD

Можно рекомендовать следующий алгоритм выполнения работы с использованием программного продукта MATHCAD.

1.Выписать из таблицы данные для одного статистического ряда.

2.Загрузить MATHCAD. Набрать m:=30(m – объем выборки или количество вариант в данном статистическом ряду), А:=. На математической палитре выбрать «Векторы и матрицы». Сформировать свой вектор, задав число строк матрицы, равное 1, а число столбцов, равное объему выборки. При вводе чисел в матрицу используйте клавишу “Tab” или мышь.

3.Для удобства преобразуем вектор-строку А в вектор-столбец Х. Для этого наберем ниже x:=A^T с помощью палитры «Векторы и матрицы», выбрав там операцию транспонирования.

4.Для того чтобы построить дискретный вариационный ряд отсортируем данные в порядке возрастания: x1:=sort(x). Чтобы вывести результат напишем x1^T=, нажмем клавишу «Enter» или щелкнем левой кнопкой мыши в произвольном месте, рядом со знаком равно получим результат. По получившейся таблице составим вариационный ряд, подсчитывая вручную частоты вариант. Наберем М1:=. Используя палитру «Векторы и матрицы» сформируем матрицу, состоящую из двух строк и стольких столбцов, сколько встречается различных вариант. В первую строку вводим значения вариант, а во вторую – значения соответствующих частот. Это и будет дискретный вариационный ряд.

5.Для того, чтобы построить полигон, на математической палитре выбираем палитру «Графики», а на ней «Декартов график». Заполняя рабочую область с помощью палитры «Векторы и матрицы», по оси абсцисс вводим (М1^Т)^<0>, а по оси ординат – (М1^Т)^<1>. Щелкнув мышью вне области графика, получим полигон частот.

6.Для построения интервального вариационного ряда воспользуемся формулой Стэрджеса, чтобы найти оптимальный шаг.

Введем . Выведем значение h. Округлим полученное значение до одного знака после запятой и введем его в качестве h. Посчитаем число интервалов:

и выведем его. Сформируем границы интервалов: j:=1..ml+1; x1_i:=min(xl); x2j:=x1i+h*(j-1,5).

Выведем полученные значения x1i=; x2^т=.

Подчитаем число вариант, попавших в каждый интервал:

L:=hist(x2,x1^т).

Таким образом, интервальный вариационный ряд имеет вид x1^т, L^т.

7. Для того чтобы построить гистограмму найдем относительные плотности частот, которые получим следующим образом:

. Затем на палитре «Графики» выбрать трехмерную гистограмму. В рабочей области гистограммы ввести массив L, щелкнув мышью вне графика, получим изображение гистограммы. В отчете необходимо будет проставить концы интервалов по оси Х самостоятельно.

8. Для построения кумулятивной кривой необходимо сначала получить матрицу накопленных частот. Для этого введем следующее:

g:=(M1^т^)<1>, i:= 0..0,i1 y_i= y^т=.,

где y_i – значения накопленных частот, il – количество столбцов в матрице М1.

При построении кривой воспользуемся палитрой «Декартов график». Заполняя рабочую область, по оси X введем X введем (М1^т)^)<0>, а по оси Y – g. Щелкнув мышью вне области графика, получим изображение искомой кривой.

9. Для нахождения числовых характеристик: среднего выборочного, средней выборочной дисперсии, выборочного среднего квадратичного отклонения, размаха выборки и др. необходимо ввести соответствующие формулы с помощью математической палитры и встроенных в нее палитр и рядом вывести получившиеся значения. Например,

среднее выборочное 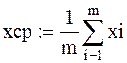xcp=;

выборочная дисперсия S*2:= S*2=;

выборочное среднее квадратичное отклонение

S*: S*=

10. 10.Для того чтобы доверительный интервал для математического ожидания при неизвестной точности измерений необходимо воспользоваться следующей формулой:

<М[x]< ,

где

- выборочная средняя;

- квантиль распределения Стьюдента;

Р – доверительная вероятность;

n – объем выборки;

S* - исправленное среднее квадратичное отклонение.

Взяв значения выборочных характеристик из п.8, а квантиль распределения из таблиц, найдем значения концов интервала ε₁, ε₂.

Пусть Р:=0,95, m:=30, t:=2,05

ε₁:= xcp- ε_1=;

ε₂:= xcp- ε_2=.

11. Для того чтобы построить доверительный интервал для дисперсии, необходимо по таблицам найти квантали распределения Пирсона и воспользоваться следующими формулами:

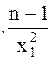S*²<D[x]< S*²или S*²<D[x]< S*²