LEARN MATHS IN ENGLISH
Изучайте математику на английском языке
Астрахань 2016
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«АСТРАХАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
КАФЕДРА АНГЛИЙСКОГО ЯЗЫКА И ТЕХНИЧЕСКОГО ПЕРЕВОДА
Л.И.Балашова, А.А.Ибрагимова
LEARN MATHS IN ENGLISH
Изучайте математику на английском языке
Учебное пособие
для студентов, обучающихся по специальностям
01.03.02 – Прикладная математика и информатика
44.03.01 – Педагогическое образование. Профиль - Математика
Издание второе,
исправленное и дополненное
Рекомендовано к печати редакционно-издательским советом
Астраханского государственного университета
Рецензенты:
кандидат филологических наук, профессор кафедры иностранных
языков гуманитарного и естественно-научного образования
Астраханского государственного технического университета,
Б.М. Тогунов
заведующий кафедрой ПТМ
Астраханского государственного технического университета,
доктор технических наук, профессор
А.Б. Филяков
Балашова Л.И., Ибрагимова А.А. Learn Maths in English - Изучайте математику на английском языке [Текст]: учебное пособие /составители Балашова Л.И., Ибрагимова А.А.- Астрахань, 2016 – стр. 78
Предназначено для студентов-математиков 1-2 курсов, владеющих основами английской грамматики. Имеет целью обеспечить их достаточным запасом лексики и лексико-синтаксических структур, необходимых при работе со специальной литературой, слушании лекций и составлении своих собственных высказываний по предмету.
ПРЕДИСЛОВИЕ
Предлагаемое пособие предназначено для студентов 1-2 курсов математического факультета, владеющих основами английской грамматики. Основной целью его является предъявление достаточного объёма лингвистического материала, необходимого в профессиональной деятельности.
Подлежащий изучению материал изложен в текстах, содержание которых соответствует программе по математике. В тексты включены основные термины определённого математического раздела (например, “NUMBERS”, “EQUATIONS” и т.п.)
Каждый текст сопровождается списком слов и словосочетаний с переводом на русский язык, что поможет учащимся быстрее ориентироваться в тексте и эффективнее использовать учебное время.
К тексту предлагаются практические задания различного типа. Их выполнение обеспечит многократную повторяемость языковых единиц, способствуя их запоминанию. Задания предусматривают не только повторение отдельных терминов, но и закрепление в сознании, затверживание набора наиболее частотных в научном стиле данной дисциплины синтаксических структур, без чего невозможно построение собственного высказывания.
Порядок расположения заданий – от более лёгкого (напр., “Find the answers in the text”) к более сложному, требующему творческого подхода в употреблении языковых средств (напр., ‘Reason your answer”, “Prove that …” и др.).
В зависимости от уровня подготовки студентов и конкретных условий преподаватель сам вправе определить место, время, способ, порядок изучения тем, добавить, сократить, изменить характер выполнения заданий, ввести новые требования, если это необходимо для достижения главной цели: научить студентов общаться на английском языке в профессиональной сфере.
Text 1
NUMBERS
The numbers we use to count objects are called whole numbers. 7 (seven), 15 (fifteen), 136 (one hundred and thirty six) are whole numbers.
For writing words we use letters, for writing numbers we use digits (or figures). There are ten digits (or figures) in mathematics. These are 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 (one, two, three, four, five, six, seven, eight, nine, nought (= zero)).
The value of the digit we define knowing its place value, i.e. its position in the number. For example, in the number 24 – the digit 2 is worth 20 (twenty), and in the number 2007 the digit 2 is worth 2000 (two thousand).
The number 4 (four) is a one-digit (= one-figure) number, 36 (thirty six) is a two-digit (two-figure) number, 145 (one hundred and forty five) is a three-digit (three-figure) number.
We read numbers in the following way:
10 – ten 20 – twenty 30 – thirty 100 – one hundred
11 – eleven 21 – twenty one 40 – forty 200 – two hundred
12 – twelve 22 – twenty two 50 – fifty 300 – three hundred
13 – thirteen 23 – twenty three 60 – sixty 400 – four hundred
14 – fourteen 24 – twenty four 70 – seventy 500 five hundred
15 – fifteen 25 – twenty five 80 – eighty 600 – six hundred
16 - sixteen 26 – twenty six 90– ninety 700 – seven hundred
17 – seventeen 27 – twenty seven 800 – eight hundred
18 – eighteen 29 – twenty eight 900 – nine hundred
19 – nineteen 29 – twenty nine 1000 – one thousand
The number 134 is read as ‘one hundred and thirty four’. The position of the ‘4’ is a place value for units. The position of the ‘3’ is a place value for tens. The position of the ‘1’ is a place value for hundreds.
The number 6,425,897 is read as ‘six million four hundred and twenty five thousand eight hundred and ninety seven’.
Vocabulary
number [′nAmbə(r)] 1/ число; количество; 2/ номер; 3/ насчитывать
to count ['kaunt] считать
object ['ObGqkt] предмет
call [kOl] называть
whole [həul] целый
whole number целое число
digit [′diGit] (= figure ['figq]) цифра
nought (=zero) [nLt] ['ziqrqu] нуль
to define [di′fain] определять
value [′vxlju:] величинa
place value [pleis ′vxlju:] поместное значение, достоинство цифры в числе
i.e. [id ′est] (= that is)  то есть
то есть
position [pə′ziS(ə)n] положение, позиция
to be worth [wə:T] обозначать величину (стоимость)
one-digit, two-digit number – одно-, двузначное число
unit [′ju:nit] единица
tens [tenz] десятки
hundreds [′hAndrədz] сотни
Task 1. Pronounce all the digits you know.
Task 2. Count a/ 11....19; b/ 21....30; c/ 20, 30….100; d/ 100, 200 ….1000.
Task 3. Read the numbers and point out units, tens, hundreds in each of them.
46, 98, 108, 234, 370, 401, 530, 657, 819, 396, 2453,5001,4209, 1809, 9531, 7030.
Task 4. Answer the questions.
1. Which numbers are called whole numbers?
2. How many digits do we know?
3. When do we use them?
4. How can we define a real value of the digit in a number?
Task 5. Give your own examples of whole numbers and point out the place value of every digit in them.
Task 6. Render the text.
Text 2
POSITIVE AND NEGATIVE NUMBERS
Numbers greater than 0 (nought = zero) are called positive numbers. They have a sign + (plus) before them. For example +2 is read ‘plus two’. Positive numbers may be written without this sign. +6 is the same as 6.
Numbers smaller than 0 (nought) are called negative numbers. They have a sign – (minus) before them. For example, -3 is read ‘minus three’.
We can show positive and negative numbers on a number line
__/___/___/___/___/___/___.___/___/___/___/___/___/__
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
The numbers to the right of zero are positive ones, and the numbers to the left of zero are negative numbers.
Positive whole numbers, negative whole numbers, and nought (= zero) are called integers.
Any positive number is bigger than any negative number.
Any negative number is smaller than any positive number.
Positive and negative numbers are sometimes known as directed numbers, or signed numbers.
Vocabulary
positive [′pOzitiv] положительный
negative [′negətiv] отрицательный
greater than ['greitq Dxn] больше чем
sign [sain] знак
plus [plAs] плюс
without [wi'Daut] (предлог) без
same [seim] то же самое
minus [′mainəs] минус
number line [′nAmbə(r) lain] числовая ось
nought [nO:t] = zero ['ziqrqu] нуль
integer [′inteGə(r)] целое число
directed number [di--, dai′rektid] направленное число
signed number [saind] число со знаком
compared with [kqm'pFqd wiD] по сравнению
Task 1. Read the numbers. Which of them are positive and which ones are negative? Why do you think so?
14, -7, +6, 322, -19, 90, 13, -251, 100, 1, -203, 1490, 2071, -1015, 2002, -1301, -538.
Task 2. Which number is bigger and which one is smaller? Why?
+5 and -40; -20 and +4; -71 and +2; 136 and 103; 48 and -15; 51 and -52; -204 and -205; 15 and +20; -7 and 27; 501 and 51; -196 and -195; +305 and +304; 5 and -2, 47 and -74, 506 and +505.
Task 3. Answer the questions.
1. Which numbers do we call positive and which negative ones?
2. What signs have positive and negative numbers before them?
3. In what way can we draw positive and negative numbers on the number line?
4. What can you say about the value of negative numbers compared with positive ones and about positive numbers compared with negative ones?
5. What is an integer?
Task 4. Give your own examples of positive and negative numbers. What can you tell about these numbers? Try to reproduce as much as possible information from Text 1 and Text 2.
Text 3
EVEN AND ODD NUMBERS
Whole numbers can be even or odd.
If a whole number can be divided by two without a remainder, it is an even number. Even numbers end in 0, 2, 4, 6 or 8.
If a whole number cannot be divided by two without a remainder, it is an odd number. Odd numbers end in 1, 3, 5, 7 or 9.
For example: The number 18 is even because it can be divided by two without a remainder (18: 2 = 9). The number 19 is odd because it cannot be divided by two without a remainder.
Vocabulary
even number [i:v(ə)n] чётное число
odd number [Od] нечётное число
to divide [di′vaid] делить
to be divided by two [di′vaidid bai tu:] делиться на два
to end (in) [end] оканчиваться
remainder [ri′meindq(r)] остаток
Task 1. Which numbers are even and which ones are odd? Reason you answer.
7, 11, 12, -56, 49, 100, 66, -15, -170, 29, 81, 37, 214, 101, 59, 208, 316, 250, 13, 97.
Task 2. Take any number and say as much as possible about it. Use the information from texts 1 and 2. Be ready to answer the questions:
1. This is a whole number, isn’t it?
2. Is it a one-digit number?
3. Is it a positive or negative number?
4. Why do you think so?
5. What sign should you write before it?
6. Is it an even or odd number? Why?
7. Where is its place on a number line? Why?
8, Can you define the place-value of every digit?
Text 4
ADDITION
In arithmetic to add two or more numbers means to find their sum, or addition may be defined as an increasing of value of one number by another one.
Algebraic addition is a combination of several algebraic expressions into a single equivalent expression.
The terms of addition are items (= addends), and the result of the operation is called the sum. The sum of two or more numbers is unchangeable regardless of the order of addition.
The sign of addition is the plus sign ‘+’
For example: 13 + 7 = 20.
The numbers 13 and 7 are items (addends), the number 20 is the sum.
The expression is read as ‘13 plus 7 is equal to 20’
or ‘13 plus 7 equals 20’
or ‘13 and 7 is (are) 20’
or ‘13 added to 7 makes 20’.
Vocabulary
addition [ə′diSn] сложение, прибавление
arithmetic [ə′riTm(ə)tik] арифметика; арифметический
to add [xd] прибавлять; складывать
to mean [mi:n] (meant, meant) значить
sum [sAm] сумма
to define [di′fain] определять
increase [in′kri:s] возрастать
combination ["kəmbi′neiS(ə)n] сочетание, соединение
several ['sevrql] несколько
algebraic [xlGi′breiik] алгебраический
expression [ik′spreS(ə)n] выражение
single [siNgl] единый; единственный; один
equivalent [i′kvivələnt] эквивалентный, равноценный
term [tə:m] член
item [′aitəm] слагаемое
addend [ə′dend] слагаемое
result [ri′zAlt] результат
operation ["Opə′reiS(ə)n] действие
unchangeable [An′CeinGib(ə)l] неизменный
regardless [ri′gRdlis] независимо от, несмотря на
order [′Ldə(r)] порядок
equal [′i:kwəl] равный
to describe [dis'kraib] описать
definition [defi'niSn] определение
Task 1. Read the examples. Call the terms of the operations.
2 + 5 = 7; 10 + 4 = 14; -11 + 6 = -5; 3 + 9 = 12; 107 + (-28) = 79; 1004 + 249 =1253, 151 + 99 = 250; -207 + 13 = -194; 97 + 58= 155; 173 + 18 =191; 1007 + 25 = 1032; 108 + 19 = 127; -59 + 307 = 248; 715 + (-507) = 208; 337 + 5 = 342; -2060 + 278 = = -1782.
Task 2. Give the definitions of the terms of addition.
Task 3. Give your own examples of addition and describe them using the words from the text.
Example: 15 + 6 = 21 – Fifteen plus six equals twenty one. This operation is called addition. The numbers 15 and 6 are items (= addends). The number 21 is the sum, the result of the operation.
Task 4. Render the text.
Text 5
SUBTRACTION
The opposite operation to addition is subtraction. It’s the mathematical process of finding the difference between the two numbers or quantities.
The terms of subtraction are minuend, subtrahend and difference.
A minuend is a number from which we subtract another number.
A subtrahend is a number which we subtract from another one.
A difference is the amount by which one quantity differs from the other.
The sign of subtraction is the minus sign (‘-‘).
For example: 11 – 6 = 5.
The number 11 is the minuend, the number 6 is the subtrahend, the number 5 is the difference.
We read it as ‘11 minus 6 is equal to 5’
or ‘11 minus 6 equals 5’
or ‘difference between 11 and 6 is 5’.
If we want to check the result, we should use addition. Difference plus subtrahend are equal to minuend.
Vocabulary
to subtract [səb′trxkt] вычитать
subtraction [səb′trxkS(ə)n] вычитание
opposite ['Opqzit] противоположный
difference [′difrəns] разность
between [bi'twi:n] между
quantity [′kwOntiti] количество
minuend [′mi:njuənd] уменьшаемое
subtrahend [′sAbtrəhend] вычитаемое
amount [ə′maunt] количество, размер
to differ [′difə(r)] отличать, различать
to check [Cek] проверять
solution [sq'lu:Sn] решение
true [tru:] верный, правильный
Task 1. Read the examples. Call the terms of the operations.
40 – 17 = 23; 100 – 80 = 20; 15 – 7 = 8; 36 – 12 = 24; 189 – 207=-18; 201 – 16= 115; 88 –57 = 31; -13 – 24 =-37; 150 – 109 = 41; 237 – 169 = 68; 13 – 340 = -327;
607 – 108 = 499; 86 – (-107) = 193; 96 – 70 = 26; -18 – 56 = - 74; 207 – (-608) = 815.
Task 2. Give the definitions of the terms of subtraction.
Task 3. Give your own examples of subtraction and describe them using the words from the text.
Example: 20 – 17 = 3. Twenty minus seventeen equals (= is equal to) three. This operation is called subtraction, it is opposite to addition. The number 20 is a minuend, from this number we subtract another number ‘–17’. The number 17 is a subtrahend, it’s the number which we subtract from 20. The number 3 is the difference, the result of this operation. If we want to check the result, we should add the difference (3) and the subtrahend (17). In our example: 3 + 17 = 20. Our solution is true.
Task 4. Render the text.
Text 6
MULTIPLICATION
Multiplication is the process of finding the number or quantity obtained by repeated additions of a specified number or quantity*
The expression 3 × 4 = 12 is read as ‘three multiplied by four equals 12’ (or ‘3 times four is 12’, or ‘3 multiplied by four is equal to 12’).
This mathematical operation is called multiplication. The number ‘3’ is the multiplicand. A multiplicand is a number that is multiplied.
The number ‘4’ is the multiplier. A multiplier is the number by which we multiply.
The number ‘12’ is the product. A product is the result of multiplication.
The numbers ‘3’ and ‘4’ (i.e. the multiplicand and the multiplier) are called factors.
The symbol ‘×’ is a multiplication sign.
* from Webster’s New World Dictionary
Vocabulary
to multiply (by) [′mAltiplai] умножать (на)
multiplication ['mAltipli′keiS(ə)n] умножение
to obtain [əb′tein] получить, достигнуть
repeated [ri′pi:tid] повторяемый
specified [′spesifaid] определённый, конкретный
multiplicand ['mAltipli"kxnd] множимое
multiplier [′mAltiplaiə(r)] множитель
product [′prOdAkt] произведение
factor [′fxktə(r)] множитель, сомножитель
time [taim] раз
each [i:C] каждый
i.e. [id'est] (= that is) то есть
Task 1. Read the expressions and call the names of each term in them.
2 × 2 = 4; 5 × 3 = 15; 8 × (-9) = -72; 4 × 6 = 24; 7 × 2 = 14; -13 × 5 = -65; 201× 4 =804; (-16) × (-3) = 48; 105 × 6 = 630; 71 × 19 = 1349; -85 × 7 = -595; 129 × 12 = 1548;
19 × (-8) = -152; 107 ×4 = 428; (-7) × (-201) = 1407; -15 × 16 = -240.
Task 2. Answer the questions.
1. What is a multiplicand?
2. What is a multiplier?
3. What is a product?
4. What is a factor?
Task 3. Complete the sentences.
1. A multiplicand is a number …
2. A multiplier is a number …
3. A product is a …
4. A multiplicand and a multiplier are called …
Task 4. Give your own examples of multiplication. Call the names of the terms in the expressions.
Task 5. Render the text.
Text 7
DIVISION
Division is the inverse operation of multiplication.
Division is the process of finding how many times a number is contained in another number (Webster’s).
The expression ‘8 ÷ 2 = 4’ is read as ‘8 divided by 2 is equal to 4’ (or ‘8 divided by 2 equals 4’).
The number ‘8’ is called the dividend. A dividend is a number that is divided.
The number ‘2’ is called the divisor. A divisor is a number by which we divide.
The number ‘4’ is called the quotient. A quotient is the result of division.
If you try to divide 7 by 2, you will see that the divisor 2 isn’t contained a whole number of times in the dividend 7. The part (1) which is left over is called remainder.
The signs -,:, ÷ are signs of division.
When the dividend is ‘0’, then the quotient is ‘0’.
We cannot divide by ‘0’. This operation is meaningless.
We can check division by using multiplication. The product of the quotient and the devisor equals the dividend.
Vocabulary
to divide (by) [di′vaid] делить (на)
division [di′viZ(ə)n] деление
inverse [in'vq:s] обратный
time [taim] раз
to contain [kən′tein] содержать
dividend [′dividənd] делимое
divisor [di′vaizə(r)] делитель
quotient [′kwəuS(ə)nt] частное
to try [trai] пытаться
part [pRt] часть
to leave [li:v] (left, left) оставлять; оставаться
remainder [ri′meində(r)] остаток
division sign [di′viZ(ə)n sain] знак деления
meaningless [′mi:niNglis] бессмысленный
obtained [qb'teind] полученный
To check the solution … чтобы проверить решение …
Task 1. Read the expressions and call the names of each term in them.
6÷ 3 = 2; 10 ÷ (-2) = -5; 18 ÷ 9 = 2; 24 ÷ 4= 6; 150 ÷ 10= 15; -237 ÷ 3 = -79;
1005 ÷ 5 = 201; 812 ÷ 29 = 28; 1580 ÷ 20 =79; -342 ÷ (-19) = 18; 3456 ÷ (-32) = -108; 156 ÷ 12 = 13; -690 ÷ 23 = -30; -954 ÷ (-9) = 106; 436 ÷ (-2) = -218, 396 ÷ 11 = 36.
Task 2. Divide these numbers by 3. Comment on the results obtained.
11 ÷ 3 =? 16 ÷ 3 =? 29 ÷ 3 =? -58 ÷ 3 =? 101 ÷ 3 =? -85 ÷ 3 =? 128 ÷ 3 =? 317 ÷ 3 =? -67 ÷ 3 =? 1008 ÷ 3 =? 172 ÷ 3 =? 301 ÷ 3 =? -1051 ÷ 3 =? 131 ÷ 3 =?
-86 ÷ 3 =? 115 ÷ 3 =?
Task 3. Answer the questions.
1. What is division?
2. What is a dividend?
3. What is a divisor?
4. What is a quotient?
5. What is a remainder?
Task 4. Complete the sentences.
1. Division is a process …
2. Dividend is a number …
3. Divisor is a number …
4. Quotient is …
5. Remainder is a part …
6. Division by nought is …
7. When the dividend is nought …
Task 5. Give your own examples of division. Call the names of terms in these operations.
Example: 6: 3 = 2. Six divided by 3 is equal to two. This operation is called division. Division is inverse to multiplication. The number 6 is the dividend. The number 3 is the divisor. The number 2 is the quotient. There is no remainder.
Task 6. Render the text.
Text 8
POWERS
One can write the products of the same number in a shorthand form by means of powers. For example: 6 × 6 = 6² (six to the power of two). 6² has the value 36.
7 ×7 × 7 = 7³ (seven to the power of three). 7³ has the value 343.
An expression of the form ‘ x × x × x × x ’ can be written as x 4 (x to the power four).
In the expressions 6², 7³, x 4 the numbers 6, 7 and x are called the base of the expression, the numbers 2, 3, 4 are called index or power. Indices can be positive or negative.
Whole numbers raised to the power 2 are called square numbers. For example: 8² = 8 × 8 = 64. 8² is read as ‘8 squared’. 64 is a square number.
Whole numbers raised to the power 3 are called cube numbers. For example: 5³ = 5 × 5 × 5 = 125. 5³ is read as ‘5 cubed’. 125 is a cube number.
Any number in the power 1 equals to its base. For example: y ¹ = y.
Any number in the power 0 equals one. For example: b º = 1.
For multiplying index forms add powers (= indices) of the same base
(a x × a y = a x+y).
For dividing index forms subtract powers (= indices) of the same base
(a x ÷ a y = a x-y).
For raising a power to a power multiply the indices: (a x)y = a xy.
When bases are different, each base must be dealt with separately.
Vocabulary
power [pauə(r)] степень
one can write можно написать
shorthand ['SO:thqnd] кратко
index [′indeks] (pl indices [′indisi:z]) показатель степени
by means of [bai mi:nz qv] посредством, с помощью
index form [′indeks fLm] остепенённое число
to raise to the power [′reiz tə Də pauə(r)] возводить в степень
base [beis] основание (степени)
square [skweə(r)] квадрат
square number число, возведённое в квадрат; квадрат числа
cube [kju:b] куб числа (третья степень)
cube number число, возведённое в куб; куб числа
to deal with [di:l wiD] (dealt) иметь дело; производить действия
separately [′sepritli] отдельно, раздельно
Task 1. Read the expressions. Name each member in them.
5², 9³, 24, 3-1, 7-5, a m-n, b x+y , 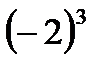 ,
, 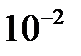 ,
, 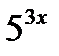 ,
, 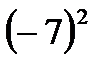 ,
, 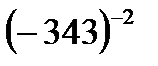 ,
, 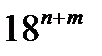 ,
, 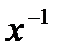 ,
, 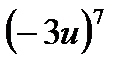 ,
, 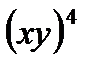
Task 2. Express the numbers in index forms.
Example: 16 = 42
16, 1000, 49, 625, -343, 512, 729, -27, 216, -243, -1000, 32, 81, -8, 121, 361.
Task 3. Give your own examples of index forms. Make some operations with them (multiplication, division). Comment on your actions.
Example: b6 × b2 =? According to the rule “for multiplying index forms add powers of the same base” we add 6 and 2 and obtain b8 . Our solution is b8 .
Task 4. Render the text.
Text 9
FRACTIONS
For correct reading fractions one should know English ordinal numerals.
Practise pronunciation:
One first eleven eleventh thirty thirtieth
Two second twelve twelfth forty fortieth
Three third thirteen thirteenth hundred hundredth
Four fourth fourteen fourteenth
Five fifth fifteen fifteenth
Six sixth sixteen sixteenth
Seven seventh seventeen seventeenth
Eight eighth eighteen eighteenth
Nine ninth nineteen nineteenth
Ten tenth twenty twentieth