Equations of the first degree are solved by different ways.
1/ Equations can be solved by method of inspection, e.g.
x – 4 = 6
x = 10
Reason: 10 – 4 = 6
3 y = 21
y = 7
Reason: 3 × 7 = 21
2/ Equations can be solved by working backwards, e.g.
x + 14 = 19
To find the value of x do opposite calculation, i.e. subtract
Solving: 19 – 14 = 5
x = 5
2 y – 1 = 7
Solving: a/ do addition 7 + 1 = 8
b/ do dividing 8 ÷ 2 = 4
y = 4
3/ Equations can be solved by balance method.
The equation remains true if you do the same to both sides of it, that is
a/ adding the same number to both sides,
b/ subtracting the same number from both sides,
c/ dividing both sides by the same number except nought,
d/ multiplying both sides by the same number.
Examples;
a + 5 = 12
Solving: subtract 5 from both sides
a = 7;
b – 2 = 8
Solving: add 2 to both sides
b = 10;
3 c + 1 = 13
Solving: subtract 1 from both sides
3 c = 12
Divide both sides by 3
c = 4
Solution of the equations can include not only whole positive numbers but negative numbers, fractions, and brackets as well.
Remember that any brackets must be removed by multiplying out before solving by balance method. This operation is called expanding. For example:
Solve: 3 (x + 4) = 21
Solving: Expand the brackets
3 x + 12 = 21
3 x = 9
x = 3
To check the solution substitute the root obtained for x in the original equation. The root is true if it fits the equation. In our example: 3(3 + 4) = 21, 7 × 3 = 21.
The root is true.
Vocabulary
way [wei] способ, метод
inspection [in′spekS(ə)n] осмотр, наблюдение, рассмотрение
reason [′ri:z(ə)n] довод, основание
working backwards [′wə:kiN ′bxkwədz] действие, решение с противоположной стороны
opposite [′Opəzit] противоположный
calculation [͵kxlkju′leiS(ə)n] расчёт, подсчёт
balance method [′bxləns ′meTəd] метод баланса, равновесия
remain [ri′mein] оставаться
except [ik′sept] за исключением, кроме
to include [in′klu:d] включать
bracket [′brxkit] скобка
to remove [ri′mu:v] удалять
as well [əz wel] также
to expand [ik′spxnd] раскрывать (скобки)
expanding [ik′spxndiN] раскрытие скобок
to check [Cek] проверять
substitute [′sAbsti͵tju:t] подставлять
to obtain [əb′tein] получать, достигать
obtained [əb′teind] полученный
original [ə′riGinl] первоначальный, исходный
to prove [pru:v] доказывать
proof [pru:f] доказательство
Task 1. Complete the sentences.
1. Equations of the first degree are solved …
2. There are three methods of solving equations. These are …
3. Solution of the equation can include …
4. The equation remains true if …
5. Any brackets must be …
6. Expanding is an operation …
7. To check the solution …
8. The root is true if …
Task 2. Solve the equations using different methods. Comment on your actions. Check the root, prove that it is true. Use the information from the text.
Example: 3x + 4 = 16 – This is a simple linear equation. It can be solved by balance method. First we subtract 4 from both sides and get 3x = 12. Then we divide both sides by 3 and obtain x = 4. Our root equals four. For checking the solution we substitute the root obtained into our original equation: 3 * 4 + 4 = 16 ® 12 + 4 = 16 ® 16 = 16. Our solution is true.
x ÷ 12 = 2; 5 c + 3 = 18; 4 b – 1 = 15; 2(y + 6) = 16; 9 x +4 = 48 – 2 x;
0,4 x +3,8 = =2,6 – 0,8 x; 6(x – 3) + 2(x +2) = 1; 0,3(6–3 y) = 4,5 – 0,8 (y – 9);
5(d – 1) –4(d – 2) = 10; 0,4 x – 2 – 1,5 x – 1 = 2,8 – 4 x;
2 x + 2 – 16 x = 20 – 12 x – 8 x – (x - 3); 1,7 – 0,3 x = 2 + 1,7 x;
(13 x – 14) – (15 + 6 x) = -3 x – 3; 
y + 9 =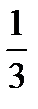 
; 
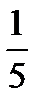(x – 3) = 
- 
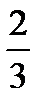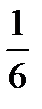(3 x – 5).
Text 16
INEQUALITIES
Expression a > b is read as ‘ a is greater than b ’.
Expression b < c is read as ‘ b is less than c ’.
Expression c ≤ d is read as ‘ c is less than or equal to d ’.
Expression d ≥ c is read as ‘ d is greater than or equal to c ’.
These are inequalities.
An inequality is a mathematical statement, such as x > o, b ≤ 2, - 4 < y < 1.
We can draw a number line to show an inequality, e.g. – 1 < 2
0 •
_/___/___/___/___.___/___/___/___/
-4 -3 -2 -1 0 1 2 3 4
The value of the numbers to the right of 0 gets bigger.
The value of the numbers to the left of 0 gets smaller.
To solve an inequality means to find the values of the unknown which make the inequality true. Methods of solving inequalities are similar to methods of solving equations.
For example:
3 x – 1 < 14
Solving: a/ add 1 to both sides
3 x < 15
b/ divide both sides by 3
x < 5
The inequality is true for all values of x which are less than 5.
Check: substitute x = 4, then 11 < 14; substitute x = 3, then 8 < 14.
So, the given inequality remains true.
Vocabulary
inequality [ini′kwOliti] неравенство
less [les] меньше
greater [greite(r)] больше
than [Dxn] чем
then [Den] затем, потом; тогда
true [tru:] верный
to remain [ri:'mein] оставаться
similar [′similə(r)] подобный
to substitute [′sAbsti͵tju:t] подставлять
given [givn] данный
Task 1. Read the inequalities.
6 < 7; -2 < 0; 11> -4; 8 > 5; a ≥ b; n ≤ m; 2 x + 1 > 7; 2(a+ 5) < a + 3; -3 x ≥ 9; -19 < 18; 15,3 >15, 03; 2 x ≥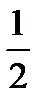 
y; 11,01 n ≤ m + 3; 59,3 > - 529; -8 (x- 2) ≥ 3 y.
Task 2. Answer the questions.
1. What is an inequality?
2. Which numbers on a number line get bigger from 0? Which ones get smaller?
3. What should you do for solving an inequality?
4. What methods of solving inequalities do you know?
5. What should you do to check the solution?
Task 3. Solve the inequalities. Comment on your actions. Check the solutions.
4 x + 2 > 0; 3 y – 5 < 1; x – 0,25(x + 4) + 0,5(3 x – 1) > 3; 4(b – 1,5) – 1,2 ≤ 6 b –1;
-4 < 2 + 3 y < 7; -2(4 z + 1) < 3 – 10 z; 4 – 3 t > -4(2 t + 2); 3 – 11 y ≤ -3(y – 2);
3 x – 5 > x +8; 6 z + 2 ≤ 3 z – 7; (5 x + 2) > 4; -3(x – 1) ≥ x + 11; 10 x + 9 > -3(2 – 5 x); 2(3 – 2 z) + 3(2 – z) ≤ 40; 12 x + 20 > 4 – 4 x; 5 b – 11 ≤ -2 b + 3.
Task 4. Give your own example. Find the solution. Reason your answer.
Text 17
SEQUENCES
Look at the list of the numbers 3, 6, 9, 12, 15… You can notice that they are ordered according to the rule ‘add 3 to find the next term’. This is a number sequence. The number 3 is the first term, the number 6 is the second term of the sequence, and so on. Sequence can be finite or infinite depending on whether it contains limited or unlimited number of terms.
A number sequence which increases (or decreases) by the same amount from one term to the next is called a linear sequence. For example, 1, 3, 5, 7, 9… In this sequence the terms increase by 2 from one term to the next, we say the sequence has a common difference of 2.
If we link the terms of the sequence by the sign ‘+’, then we obtain numerical series. The sum of the first ‘n’ terms of the series is called partial sum of the series (’n’ denotes a quantity of terms in a series).
The Greek letter Σ is the summation sign.
An important characteristic of a sequence is convergence. A sequence can be either a convergent sequence or a divergent sequence. A sequence which has a limit is convergent, otherwise it is divergent.
Vocabulary
sequence [′si:kwəns] последовательность
list [list] список
notice [′nəutis] замечать
to order [Ldə(r)] организовать, выстроить по порядку
according to [ə′kLdiN tə] в соответствии
rule [ru:l] правило
term [tə:m] член
number sequence числовая последовательность
finite sequence [′fainait] конечная последовательность
infinite sequence [′infinit] бесконечная последовательность
depending on [di'pendiN On] в зависимости
to contain [kqn'tein] содержать
limit [′limit] граница, предел
limited [′limitid] ограниченный
unlimited [An′limitid] неограниченный
to increase [in′kri:s] возрастать
to decrease [di′kri:s] уменьшаться, убывать
amount [q'maunt] количество, величина
linear sequence [′li:niə(r)] линейная последовательность
common difference ['kOmqn 'difqrqns] общая разность
to link [liNk] соединять
numerical series [nju:'merikql ′siəri:z, -riz] числовой ряд
sum [sAm] сумма
partial ['pRSql] частичный
to denote [di'nqut] обозначать
infinity [in′finiti] бесконечность
Greek [gri:k] греческий
Σ ['sigmq] сигма (греческая буква)
summation sign [sA′meiʃ(ə)n sain] знак (символ) суммы
convergence [kən′və:Gəns] сходимость
either…or…[′aiDə(r) L] или… или…
to converge [kən′və:G] сходиться
convergent [kən′və:Gənt] сходящийся
divergent [dai′və:Gənt] расходящийся
otherwise ['ADqwaiz] иначе, в противном случае
certain [sq:tn] определённый; некоторый
Task 1. Answer the questions.
1. What is a number sequence?
2. Which number sequence is called finite and which one is infinite?
3. What should you know to find the next term of the sequence?
4. What is a linear sequence?
5. What is a series?
6. What does the Greek letter Σ denote?
7. What is an important characteristic of a sequence?
8. What’s the difference between convergent and divergent sequence?
Task 2. Complete the sentences using the information of text 17, pronounce them paying attention to your pronunciation.
1. The list of numbers ordered according to the certain rule …
2. A sequence can be …
3. In a linear sequence the terms …
4. If we link the terms by the sign + …
5. An important characteristic of a sequence is …
6. A convergent sequence …
7. A divergent sequence …
Task 3. Give your own example of a sequence. Describe its properties. Be ready to answer the questions:
1. Is it a linear sequence?
2. Is it a limited or unlimited sequence? Why?
3. How many terms are there in it? Name them.
4. Does it increase or decrease from one term to the next?
5. By what rule does it ordered?
6. Can you define the partial sum of the series?
7. Is it convergent or divergent? Why?
Task 4. Ask your friend to define the rule according to which the numbers in the sequence given by you are ordered.
Task 5. Render the text.
Text 18
PROPORTIONS
The faster we are walking the less time we need to finish a definite distance and the longer distance we cover for a definite time. The slower our speed the more time we need to finish a definite distance and the shorter distance we cover for a definite time. So, we see that speed, time, and distance depend on each other. They are said to be proportional to each other.
If the ratio of the two quantities ‘ a ’ and ‘ b ’ (a: b) is always constant, then we say that ‘ b ’ varies directly with ‘ a ’, or ‘ b ’ is proportional to ‘ a ’.
We can express it using symbols: ‘ b α a ’ where ‘α’ means ‘proportional to’
The relation between ‘ a ’ and ‘ b ’ can also be expressed as an equation ‘ b = ka’ where ‘ k ’ is the constant of proportionality.
If one quantity increases and the other increases at the same rate, they are in direct proportion. In our example at constant time speed and distance are in direct proportion.
If one quantity (‘ a ’) increases and the other quantity (‘ b ’) decreases at the same rate, these quantities are in inverse proportion.
In this case ‘ b’ varies directly with 1/ a, or we may say ‘ b ’ is inversely proportional to a. It can be expressed by symbols as ‘ b α 1/ a’.
The relationship between ‘ a ’ and ‘ b ’ can also be expressed as an equation: b = k/a where ‘ k ’ is the constant of proportionality.
In our example at constant distance speed and time are in inverse proportion.
The general form of a proportional relation is y α xn or y = kxn .
Vocabulary
proportion [prə′pLS(ə)n] пропорция
fast [fRst] быстрый
definite [′definit] определённый
distance [′distəns] расстояние
speed [spi:d] скорость
to cover ['kAvq] = to finish
slow [sləu] медленный
to depend (on) [di′pend] зависеть (от)
they are said to be … говорят, что они …
proportional [prə′pLSən(ə)l] пропорциональный
ratio [′reiSiəu] отношение, пропорция
quantity [′kwOntiti] количество
constant ['kOnstqnt] постоянный
proportionality [prə"pLSə′nxliti] пропорциональность
to vary [′veəri] изменяться
directly [dai-, di′rektli] прямо
to express [iks'pres] выразить
symbol [′simb(ə)l] символ, знак
relation [ri′leiSən] отношение
to increase [in′kri:s] возрастать
at the same rate [seim reit] на ту же самую величину
to be in direct proportion быть прямо пропорциональным
at constant time (distance) при постоянном времени (расстоянии)
to decrease [di′kri:s] уменьшаться, убывать
to be in inverse proportion [in′və:s prə′pLSn] быть обратно пропорциональным
inversely proportional обратно пропорциональный
in this case [keis] в этом случае
relationship [ri′leiSənSip] отношение
general ['Genqrql] общий
Task 1. Practise pronunciation:
Fast, slow, definite, ratio, proportion, proportional, proportionality, quantity, vary, directly, relation, relationship, increase, decrease, distance, inverse, inversely, general.
Task 2. Describe the relationship between two quantities when they are in direct proportion.
Task 3. Describe the relationship between two quantities when they are in inverse proportion.
Task 4. What can you say about the relationship between circumference and radius in a circle? Between length and width in rectangles of constant area?
Between the amperage and voltage? Between resistance and current? Between gravity and mass of bodies? Between the strength of the interaction (Coulomb force) and the distance between charged bodies? Between the density and body volume? Between mass and volume of the body?
(Сила тока и напряжение, сопротивление и сила тока, сила притяжения и массы тел, сила взаимодействия (сила Кулона) и расстояние между заряженными телами, плотность и объем тела, масса и объем тела.)
Task 5. Give an example of values which are in inverse proportion. Express their relationship in words, in symbols, and as an equation.
Task 6. Give an example of values which are in direct proportion. Express their relationship in words, in symbols, and as an equation.
Task 7. Render the text.
Text 19
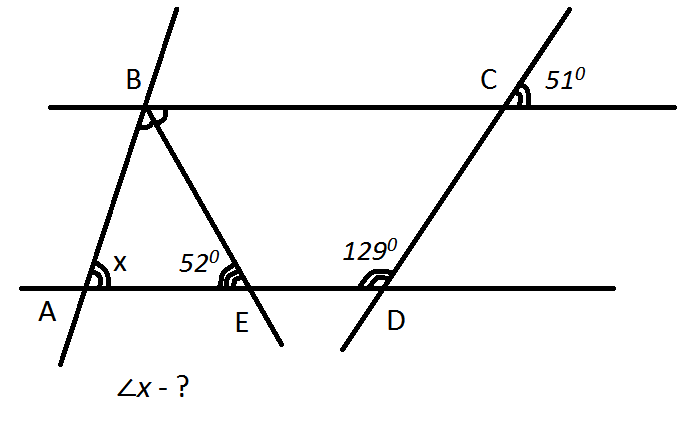
ANGLES
An angle is regarded as the measure of turn (= rotation). An angle is formed by two lines (sides) meeting at a point which is called vertex.
Angles are measured in degrees. There are several types of angles according to their measure.
Null (=zero) angle = 0º
Acute angle is between 0º and 90º.
Right angle = 90º. Its sides are perpendicular to each other.
Obtuse angle is between 90º and 180º.
Flat (= straight) angle = 180º.
Reflex angle is between 180º and 360º.
Round angle (= perigon) = 360º.
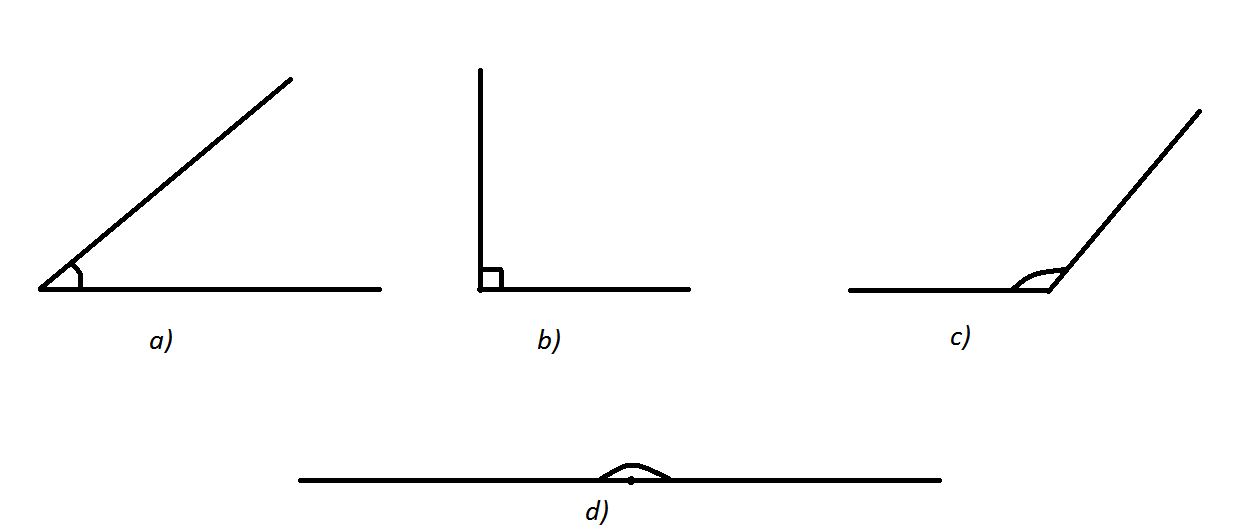
fig.1
Complementary angles are formed inside the right angle by a straight line drawn from its vertex.
Supplementary angles are formed inside a flat angle by a straight line drawn from its vertex.
Vertically opposite angles are formed by two crossing straight lines.
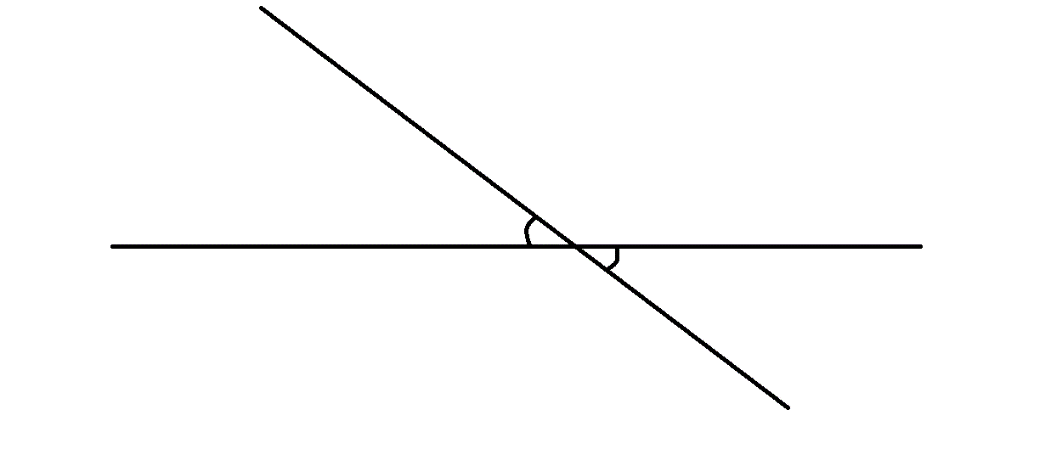
fig.2
Angles at a point are located between straight lines drawn from one point in different directions.
Corresponding angles are always on the same side of the transversal.
Transversal is a straight line crossing two parallel lines.
Alternate angles are on the opposite sides of the transversal.
Allied angles are on the same side of the transversal.
A rotation angle is positive if measured in an anticlockwise sense and negative if in a clockwise sense.
Angles are usually identified by using three capital letters, where the middle letter is a vertex (e.g. A B C). Or you can use small letters to mark the angle (a, b …)
A straight line halving an angle is called bisectrix (= bisector).
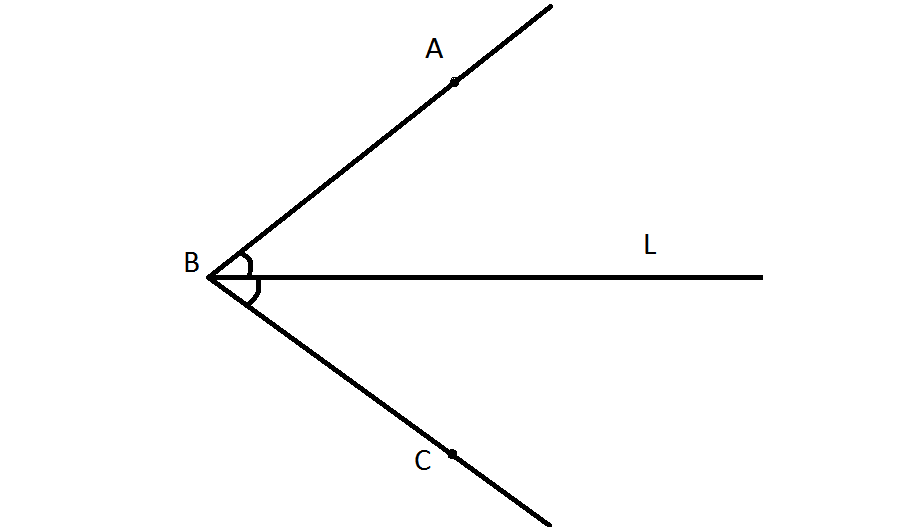
fig.3
Vocabulary
angle [xNg(ə)l] угол
to be regarded [ri′gRdid] считаться, рассматриваться (как)
measure [′meZə(r)] измерять; мера
to be measured [′meZəd] измеряться
turn [tə:n] (= rotation [rəu′teiS(ə)n]) вращение; поворот
to be formed образоваться
side [said] сторона
vertex [′və:təks] (pl vertices [-tisiz]) вершина
degree [di′gri] градус
types of angles: [taips] типы углов
null [nAl] нулевой
acute [ə′kju:t] острый
right [rait] прямой
perpendicular [pq:pqn'dikjulq(r)] перпендикуляр; перпендикулярный
obtuse [əb′tju:s] тупой
flat [flxt] развёрнутый
reflex [ri'fleks] угол в пределах 180º и 360º
round [raund] angle (= perigon [′perigən]) полный угол (360º)
complementary [͵kOmpli′mentəri] дополнительный (до 90º)
inside [in'said] внутри
straight [streit] прямая
supplementary [͵sAplə′mentəri] смежный, добавочный, дополнительный (до 180º)
to draw [drL] (drew, drawn [drLn]) начертить, провести линию
vertically opposite [′və:tikəli ′Opəzit] вертикально противоположный
to cross [krOs] пересекать
angles at a point [xNglz ət ə point] углы между прямыми, проведёнными из одной точки в разных направлениях
to locate [′ləukeit] помещать, располагать
to be located находиться
direction [di'rekSn] направление
corresponding [͵kOris′pondiN] соответственный
transversal [͵trxns′və:s(ə)l] поперечный; пересекающий, секущий
alternate [Ll′tə:nət, Ol-] накрест лежащий
allied [ə′laid] внутренние односторонние
positive [′pɔzitiv] положительный
negative [′negətiv] отрицательный
anticlockwise sense [͵xnti′klOkwaiz sens] против часовой стрелки
clockwise sense [′klOkwaiz sens] по часовой стрелке
to identify [ai′dentifai] определять
to halve [hRv] делить пополам
middle [midl] средний, середина
to mark [mRk] отмечать, помечать
bisectrix [bai′sektris] (= bisector [bai′sektə(r)]) биссектриса
to describe [dis'kraib] описывать
hence [hens] следовательно
Task 1. Complete the sentences.
1. An angle equals 00 ….
2. An angle equals 300 …
3. An angle equals 900 …
4. An angle equals 1200 …
5. An angle equals 1800 …
6. An angle equals 2100 …
7. An angle located inside the right angle …
8. An angle located inside the flat angle …
9. Angles formed by two crossing lines …
10. Transversal is …
11. A rotation angle is positive …
12. A rotation angle is negative …
13. Angles are identified …
14. Bisector is …
Task 2. Define the types of the angles. Describe their properties.
Example: Angles DBC and ABD (fig.a) are supplementary angles. They are formed inside the flat angle ABC by a straight line BD drawn from its vertex. We identify our right angle by three capital letters, and complementary angles by small letters e, f. The line BL is a bisectrix of angle DBC, it haves it. We can define the measure of these complementary angles. Right angle equals 900,hence angles e and f equal 450 (forty five degrees).
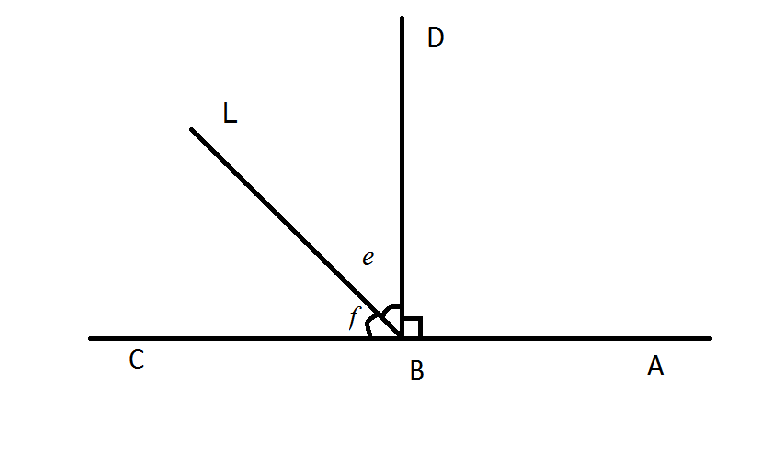
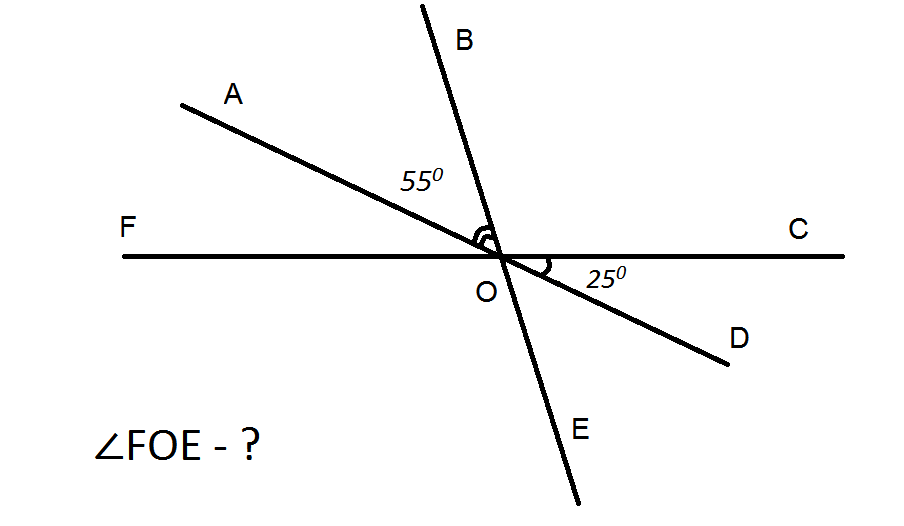
a) b)
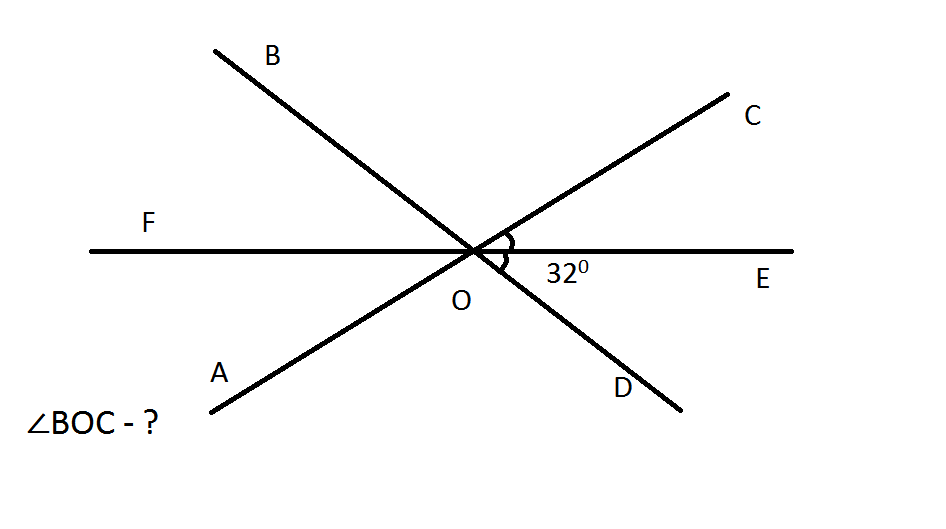
c) d)
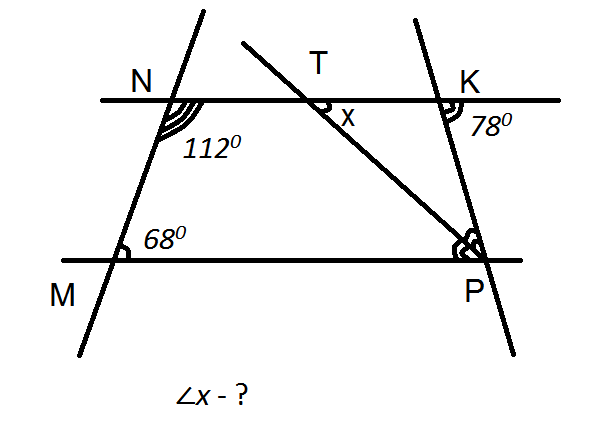
e) f)
fig.4
Task 3. Learn the definitions of angles by heart.
Text 20
TRIANGLES
A shape made by three or more points (vertices) joined by line segments (sides) is called polygon. One of such figures is a triangle. It is formed by three line segments. The number of sides is equal to the number of interior angles. The sum of these angles is 180º. Short for triangle is symbol ∆.
There are some different types of triangles.
Acute angled ∆ has three acute angles.
Obtuse angled ∆ has an obtuse angle.
Right angled ∆ has a right angle.
In scalene ∆ all angles and lengths of sides are different.
Isosceles ∆ has two equal sides and two equal angles.
In equilateral ∆ all sides are equal and each of three angles is 60º.
An exterior angle formed by extending one side of a triangle is always equal to the sum of the two opposite interior angles.
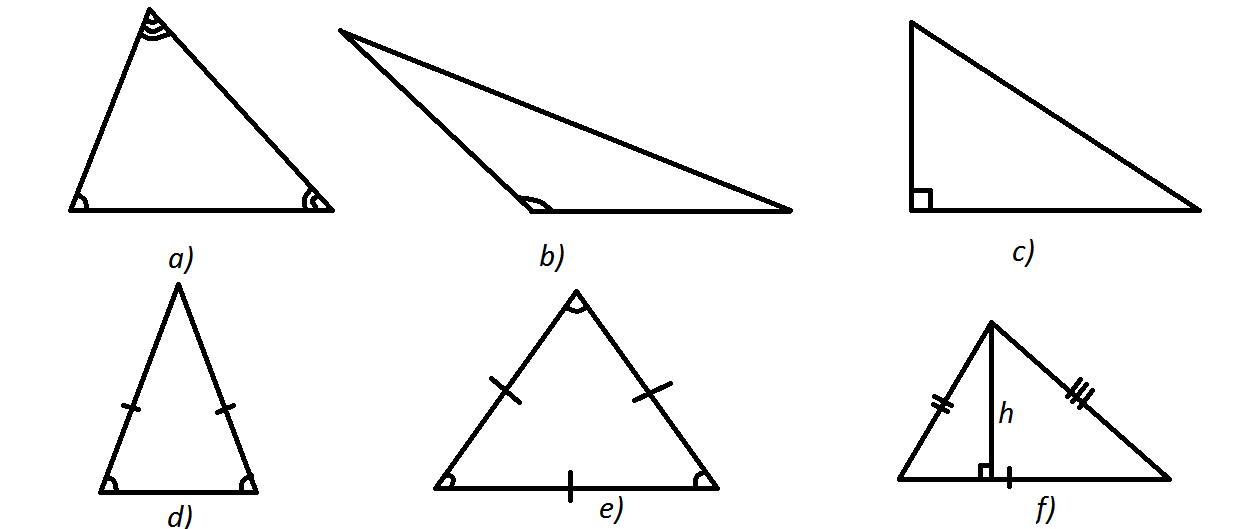
fig.5
A perpendicular dropped from the vertex of the ∆ onto its side is the height of the triangle. A straight line segment from the vertex onto the middle of the opposite side is a median.
To find area of any ∆ multiply the length of its side by its height and divide the product by two.
Vocabulary
triangle [′trai͵xNgl] треугольник
shape [Seip] форма
vertex [vq:teks] (pl. vertices) вершина
to join [GOin] соединять, присоединять
line segment [lain segment] отрезок прямой
side [said] сторона
polygon [′pOligən] многоугольник
such [sAC] такой
interior angle [in′tiəriq(r)] внутренний угол
types of triangles типы треугольников
acute angled [ə′kju:t xNgld] остроугольный
obtuse angled [əb′tju:s xNgld] тупоугольный
right angled [rait xNgld] прямоугольный
scalene [′skeili:n] разносторонний
length [leNgT] длина
isosceles [ai′sOsi͵li:z] равнобедренный
equilateral [͵i:kwi′lxtər(ə)l] равносторонний
60º [′siksti di′gri:z] 60 градусов
exterior angle [ik′stiəriə(r)] внешний угол
to extend [ik′stxnd] удлинять
sum [sAm] сумма
opposite ['Opqzit] противоположный
to drop a perpendicular [drOp pə:pən′dikjulə(r)] опустить перпендикуляр
height [hait] высота
median [′mi:diən] медиана
area [′eəriə] площадь
property ['prOpqti] свойство
describe [di'skraib] описывать
to prove [pru:v] доказать
proof [pru:f] доказательство
Task 1. Answer the questions.
1. What is a triangle?
2. What is the property of interior angles for any triangle?
3. What types of triangles do you know?
4. What is the size of the exterior angle?
5. What is the height of the triangle?
6. In what way can you find an area of any triangle?
Task 2. Look at the triangles. Identify their types and describe their properties
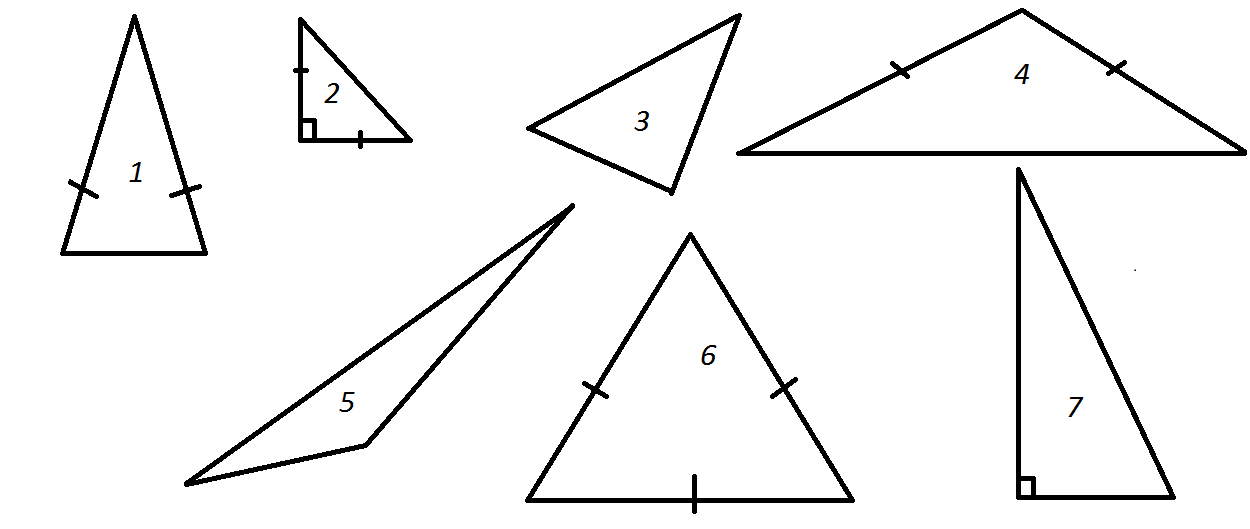
Task 3. Solve the problems.
For proving theorems and solving problems you may need some of these words and expressions: given - данный, дано
find - найдите
hence - следовательно
consequently - следовательно
then - затем, тогда
if … then - если … то …
so - итак, поэтому
by the formula - по формуле
according to the rule - согласно правилу
suppose - предположим
assume - допустим
as we know - как мы знаем
it is known that - как известно
Example: Given: ∆ ABC
Ð BAC = 1100
Ð BCA = 200
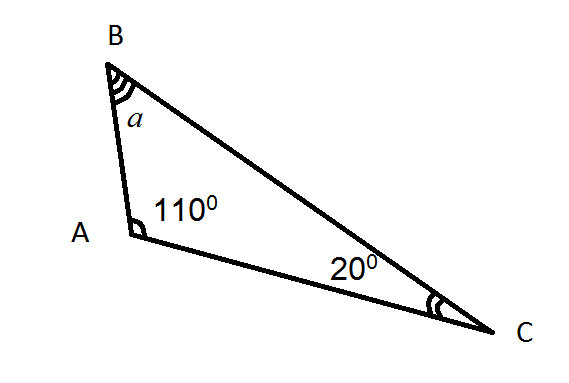
Find: Ð a
Solving: It is known that the sum of interior angles of any triangle is 1800 . We are given measures of the two angles. Their sum equals 1300 (1100 + 200). Then we subtract this number from 1800 and get 500. So, Ð a equals 500.
Task 3. Find all unknown angles in ∆ ABC:
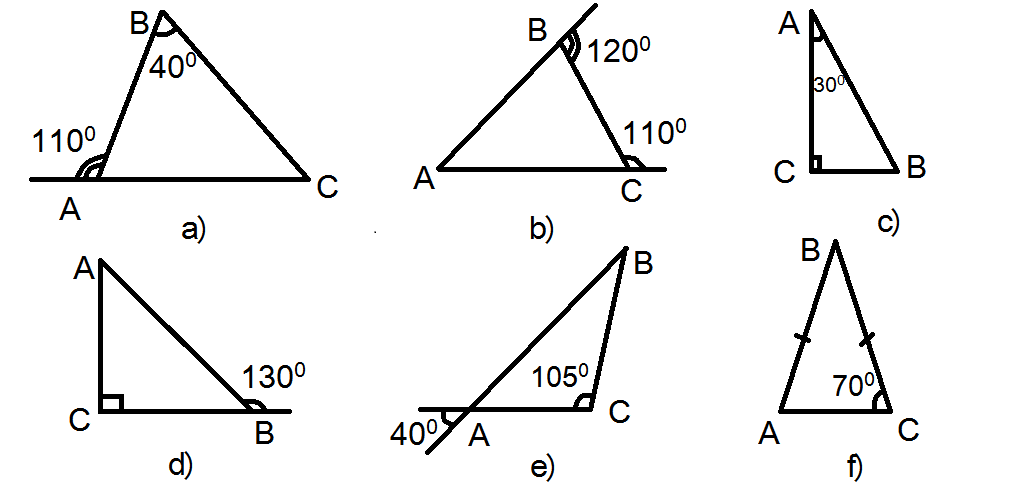
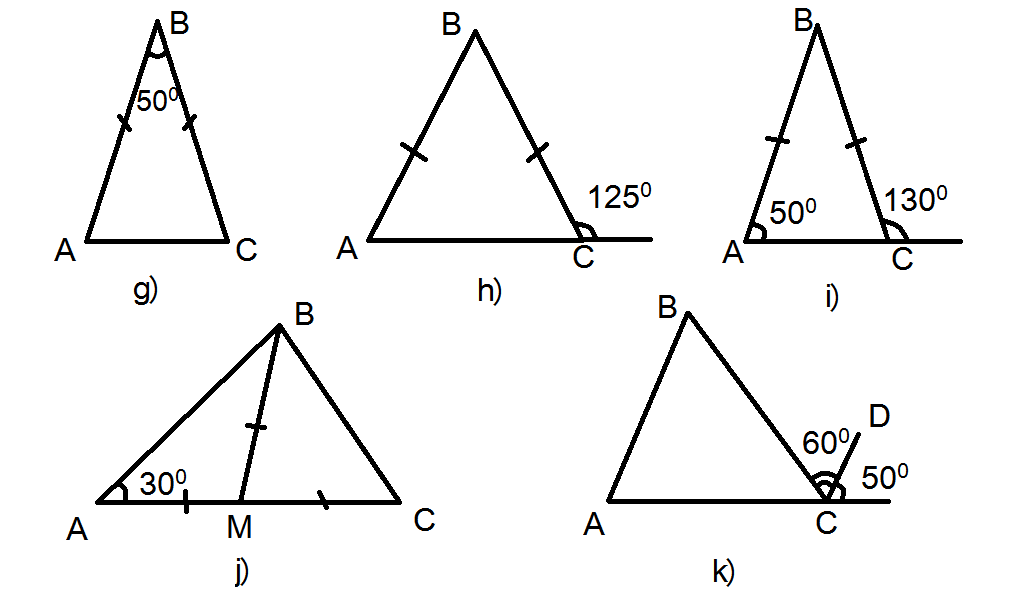
Task 4. Prove the statement about the size of the exterior angle.
Text 21
QUADRILATERALS
Aquadrilateral is a four-sided polygon. The number of sides is equal to the number of interior angles, i.e. four. The sum of the four angles is 360º.
Square is a quadrilateral which has four equal angles, each one of 90º. All four sides of the square are equal and opposite sides are parallel. Diagonals of the square bisect each other at 90º.
Rectangle is a quadrilateral with four equal angles of 90º. Its opposite sides are equal and parallel.
Parallelogram is a four-sided polygon where opposite angles are equal and opposite sides are equal and parallel.
Rhombus is a quadrilateral in which all four sides are equal, opposite angles are equal, and opposite sides are parallel. Diagonals bisect each other at 90º.
Trapezium is a four-sided shape with one pair of parallel sides.
Kite is a quadrilateral where one pair of opposite angles are equal, two pairs of adjacent sides are equal, and one diagonal crosses the other at 90º.
Quadrilaterals are usually identified by using capital letters.
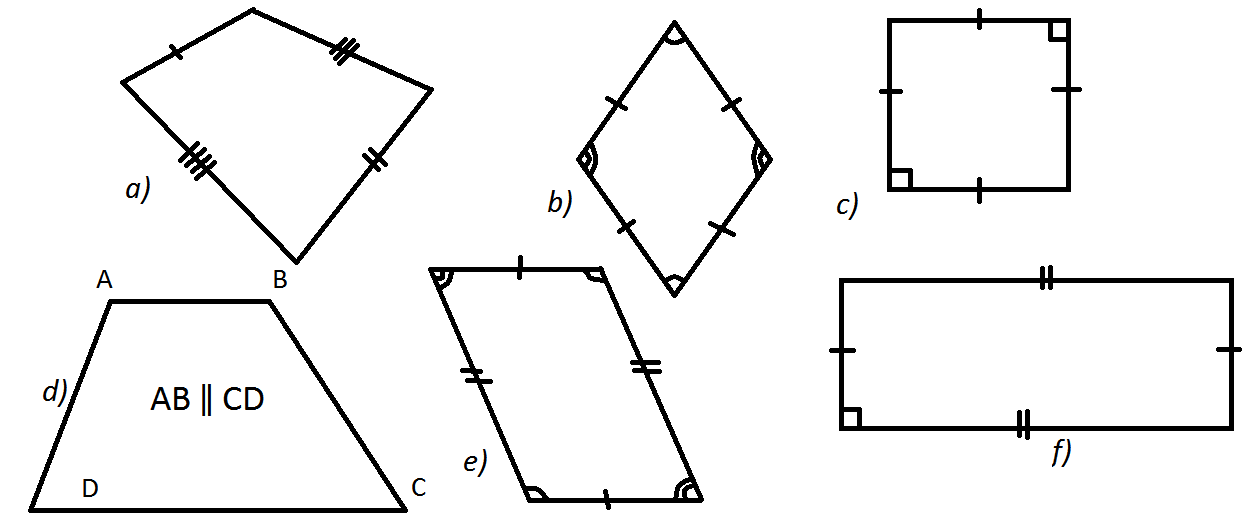
fig.6
To find an area of a square multiply together amount of two sides.
To find an area of a rectangle multiply the length by the width.
To find an area of a parallelogram multiply its side by its height. Height is
a perpendicular drawn from the vertex onto the side.
Vocabulary
quadrilateral [͵kwOdri′lxtər(ə)l] четырёхсторонний; четырёхсторонняя фигура
polygon [′pOligən] многоугольник
three-sided [Tri: ′saidid] трёхсторонний
four-sided [fL ′saidid] четырёхсторонний
i.e. [id′est] (= that is) то есть
each [i:C] каждый
diagonal [dai′xgən(ə)l] диагональ
to bisect [bai′sekt] (= to cross) пересекать
each other [i:C ADə] друг друга
rectangle [rek′txNg(ə)l] прямоугольник
parallelogram [͵pxrə′lelq͵grxm] параллелограмм
rhombus [′rOmbəs] ромб
trapezium [trə′pi:ziəm] трапеция
pair [peə] пара
kite [kait] змей
adjacent [ə′Geis(ə)nt] смежный
to identify [ai′dentifai] опознавать, определять
amount [ə′maunt] размер; количество
length [leNgT] длина
width [widT] (= breadth) ширина
height [hait] высота
to draw [drL] (drew, drawn) чертить; рисовать
work out вычислить
Task 1. Find the answers to the questions in the text.
1. How many sides have quadrilaterals?
2. What can you say about the number of interior angles in a quadrilateral?
3. What is the sum of interior angles in a quadrilaterals?
4. What should you do to find an area of a square? Rectangle? Parallelogram?
Task 2. Identify and describe the properties of each kind of quadrilaterals using the information from the text.
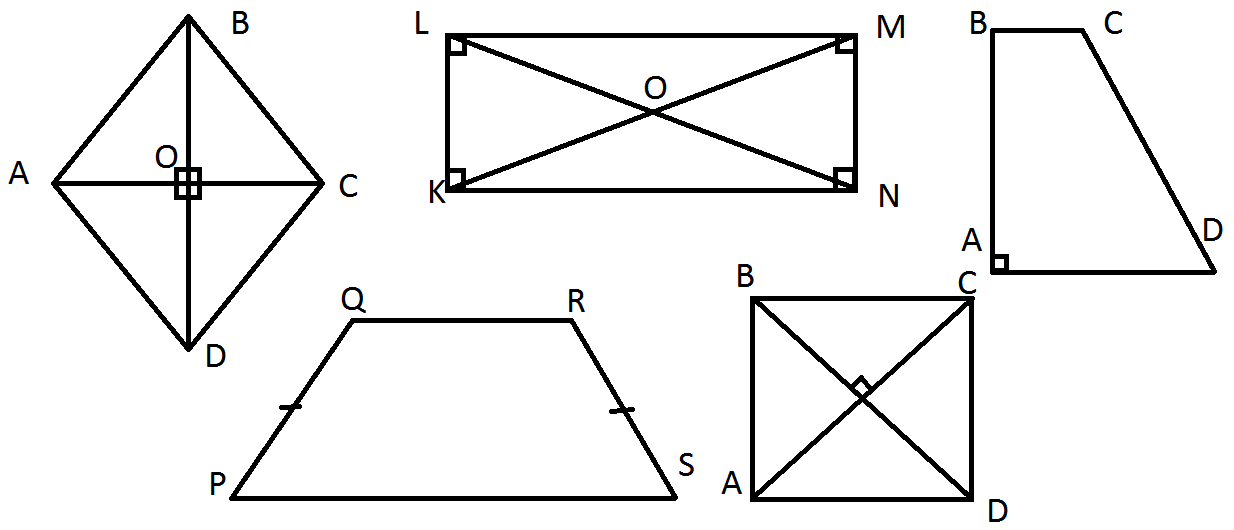
Task 3. Describe properties of any quadrilateral and ask your friend to draw it on the blackboard.
Task 3. Work out areas of the figures knowing the size of sides. Comment on your answer.
a/ Square: 1) the length of the side - 4 cm; 2) the diagonal – 6 cm; 3) the perimeter – 32 m; 4) the length of the side – 15 cm.
b/ Rectangle: 1) the length – 13 cm, the width – 3 cm; 2) the length – 6 cm, the perimeter – 18 cm, 3) the width – 4 m, the length of 2 times more, 4) the length – 18 cm, the width is 3 times smaller.
c/ Parallelogram: 1) the length of a side – 10 cm, the height – 2.5 cm; 2) the length of a side – 2 cm, the height – 8 cm.
Task 4. Explain in what way one can find areas of rhombus, trapezium, and a kite.
Text 22
POLYGONS
A polygon is a shape made by three or more points (vertices) joined by line segments.
A three-sided polygon is a triangle.
A four-sided polygon is a quadrilateral.
A five-sided polygon is a pentagon.
A six-sided polygon is a hexagon.
An eight-sided polygon is an octagon.
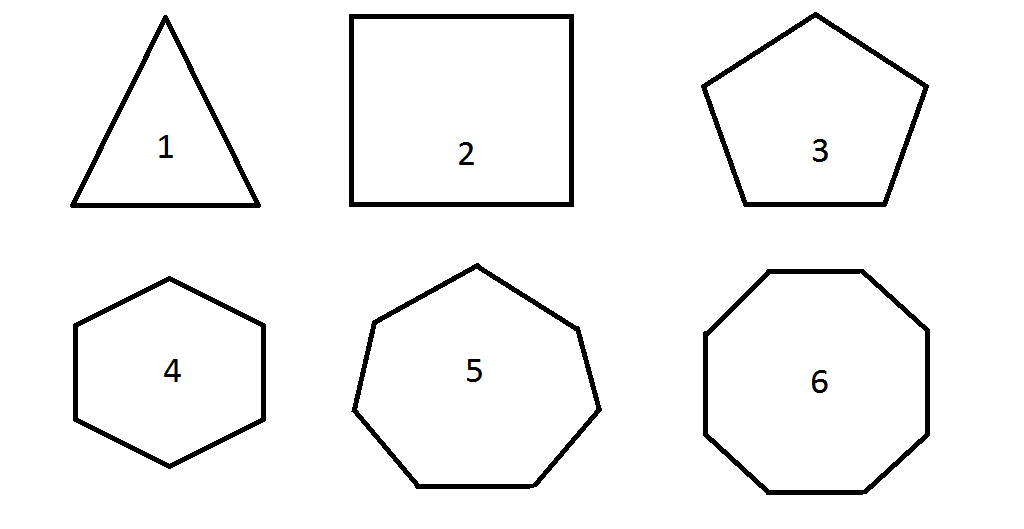
fig. 8
It is easy to work out the sum of interior angles of any polygon. Draw diagonals from one vertex. The sum of angles of each triangle is 180º. Multiply 180º by the number of triangles obtained. So, the sum of interior angles of pentagon is 540º, of hexagon - 720º, etc.
In general, for any n- sided polygon, the sum of the interior angles is (n – 2) × 180º.
Substitute the number of sides instead of ‘ n ’ and get the necessary sum.
A polygon where all sides and angles are equal are called regular. For any regular n -sided polygon an exterior angle equals 360º/ n.
The distance from the centre of a regular polygon to one of its vertices is called the long radius. The perpendicular distance from the centre to one of the sides is called the short radius which is also the radius of the inscribed circle of the polygon.
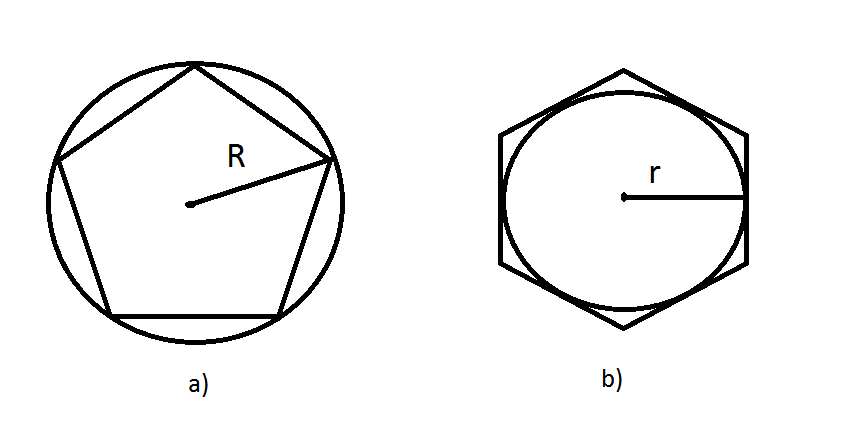
fig. 9
The polygon is convex if all the interior angles are less than or equal to 180º.
The polygon is concave if it has one or more interior angles greater than 180º.
Vocabulary
polygon [′pOligən] многоугольник
shape [Seip] форма
to join [GOin] присоединять, соединять
pentagon [′pentəgən] пятиугольник
hexagon [′heksəgən] шестиугольник
octagon [′Oktəgən] восьмиугольник
so [squ] зд.: следовательно
to work out [wə:k aut] вычислять
to obtain [əb′tein] получать; достигать
in general [in ′Genər(ə)l] в общем виде
to substitute [′sAbsti͵tju:t] подставлять
instead of [in′sted əv] вместо
to get (got) [get] достигать, получать
regular [′regjulə(r)] правильный
distance [′dist(ə)ns] расстояние
radius [′reidiəs] (pl radii) радиус
inscribed circle [in'skraibd sq:kl] вписанная окружность
convex [′kOnveks] выпуклый
concave [′kOnkeiv] вогнутый
Task 1. Complete the sentences.
1. A triangle is a …
2. A quadrilateral is a …
3. A pentagon is a …
4. A hexagon is a …
5. An octagon is a …
6. The sum of angles in a triangle is …
7. The sum of angles in a pentagon is …
8. The sum of interior angles for any n-sided polygon …
9. In regular polygon all sides and angles …
10. The long radius is the distance from …
11. The short radius is the perpendicular distance …
12. In convex polygon all interior angles are …
13. In concave polygon one or more interior angles are …
14. In any regular n-sided polygon exterior angle …
Task 2. Answer the questions.
1. What is a polygon?
2. What types of polygons do you know?
3. What should you know to work out the sum of interior angles of a polygon?
4. What is the formula for working out the sum of interior angles for any n-sided polygon?
5. What is the sum of interior angles for a triangle? A quadrilateral? A pentagon? A hexagon?
6. Which type of polygon is regular?
7. What is the amount of the exterior angle for any regular polygon?
8. What is a long radius?
9. What is a short radius?
10. What can you say about the angles of concave polygon?
11. What can you say about the angles of convex polygon?
Task 3. Identify the types of polygons and say as much as possible about their properties.
Example: This is an octagon, eight-sided polygon. The sum of interior angles according to the formula (8 – 2)* 180 equals 10800 . This polygon is regular, all its sides and angles are equal. It is convex, because interior angles are less than 1800 . The line OB is a long radius. The line OC is a short radius, it is also a radius of an inscribed circle. The size of an exterior angle by the formula 360/n equals 400 .
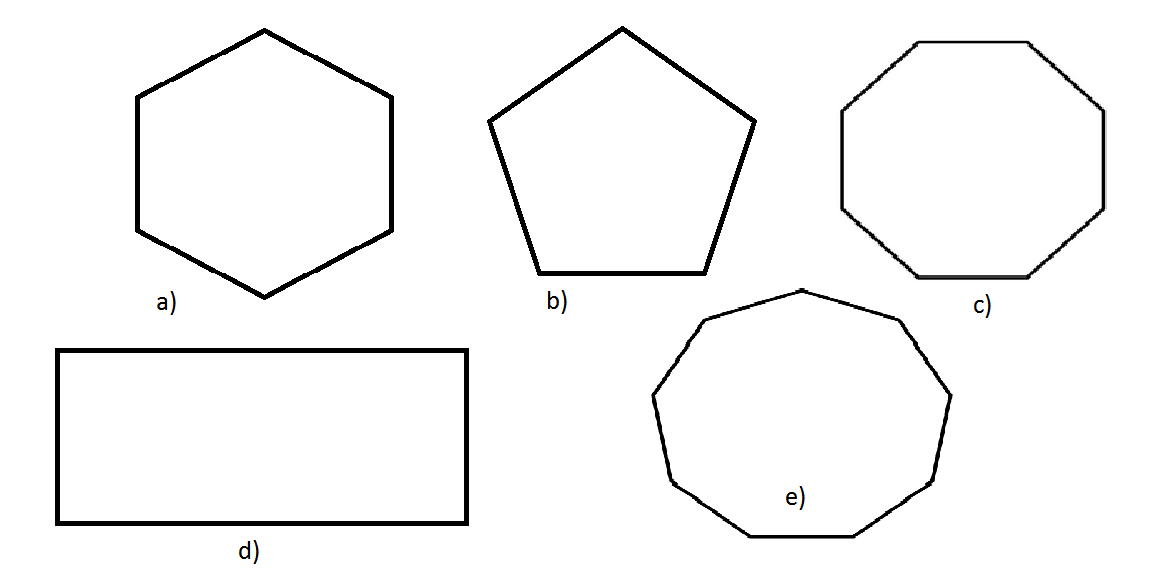
fig.10
Text 23
PYTHAGOREAN THEOREM
Theorems are geometrical facts, or properties. To prove the required facts take the facts which are assumed to be true and then by means of them deduce other facts eventually leading to the proof of the required facts. Later, if necessary, this proved fact can be used as true for solving and proving other facts.
For example, Pythagorean Theorem: “The square on the hypotenuse i s equal to the sum of the squares on the other two sides”.
Hypotenuse is the longest side in a right-angled triangle.
So, if you know the length of the hypotenuse and one side (cathetus) in a right-angled triangle, you can work out its other side (cathetus).
Let’s name the hypotenuse (= hyp) by the letter a, two other sides by letters b and c. Then Pythagorean Theorem can be written as a formula a2 = b2 + c2.
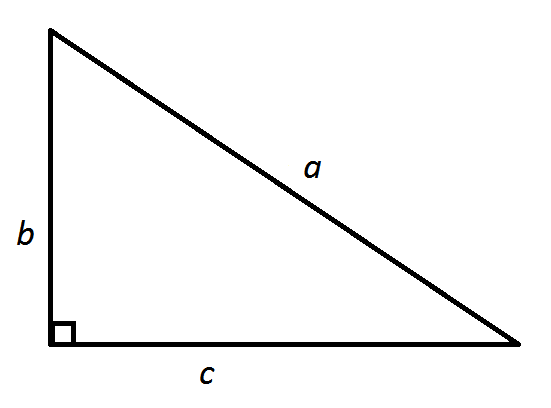
fig.11
Vocabulary
Pythagoras [pai'Txgqrqs] Пифагор
Pythagorean theorem [pai"Txgq'riqn ′Tiərəm] теорема Пифагора
geometrical fact [͵Giə′metrik(ə)l fxkt] геометрический факт
property [′prOpəti] свойство
to prove [pru:v] доказывать
proof [pru:f] доказательство
required fact [ri′kwaiəd] требуемое доказательство, нужный результат
to assume [ə′sju:m] предположить; принять (за)
by means of [bai mi:nz əv] с помощью
to deduce [di′dju:s] вывести, сделать вывод
eventually [i′ventjuəli] в конечном счёте, в итоге; в конце концов
to lead [li:d] (led) приводить
later [leitq] позднее
necessary ['nesqsqri] необходимый
hypotenuse [hai′pOtənju:s] гипотенуза
cathetus [′kxTətəs] катет
to work out [wə:k aut] вычислять
to calculate [′kxlkju͵leit] вычислять, подсчитывать
we are given дано
to suppose [sə′pəuz] предполагать
let’s name давайте назовём
formula [′fLmjulə] (pl formulae [-li:], formulas) формула
Task 1. Learn Pythagorean Theorem by heart.
Task 2. We are given the length of two sides of right-angled triangle: 4 cm and 5 cm. Calculate the length of the hypotenuse (= hyp) using Pythagorean Theorem. Reason your answer.
Task 3. Calculate the length of the other cathetus if you are given: a) hyp = 10 cm, the cathetus = 6 cm; b) hyp = 41 m, the cathetus = 40 m; c) hyp = 17 cm, the cathetus = 8 cm. Reason your answer.
Calculate the hypotenuse if you are given: a) cathetus = 4 and 3 cm; b) cathetus = 24 and 7 cm; c) cathetus = 5 and 12 cm. Reason your answer.
Task 4. Suppose the height of the house is 8 meters. Work out the length of the inclined ladder* you need to get to the roof**. What else value you ought to know? Comment on your answer.
* inclined ladder наклонная лестница
** roof крыша
Task 5. Give your own examples of using Pythagorean theorem.
Text 24
CIRCLE
Circle is a shape formed on a plane by a line lying on the same distance from a fixed point. We can draw a circle using a compass (= pair of compasses).
Perimeter of a circle is its circumference (= C).
Distance from the centre of the circle to any point on the circumference is called radius (= r).
Space between two radii is a sector.
Distance right across the circle passing through the centre is the diameter (= d). It is twice as long as the radius.
Diameter divides a circle into two semi-circles.
A line joining two points on the circumference is called a chord. A chord divides a circle into two segments.
A line touching a circumference at one point is called tangent. It is perpendicular to the radius at the point of contact.
A part of the circumference is called an arc.
The circumference of any circle equals its diameter multiplied by the number π. An approximate value for ‘π’ is 3.14, i.e. C = π × d.
The area of a circle equals its radius squared multiplied by π, i.e. A = π × r2.
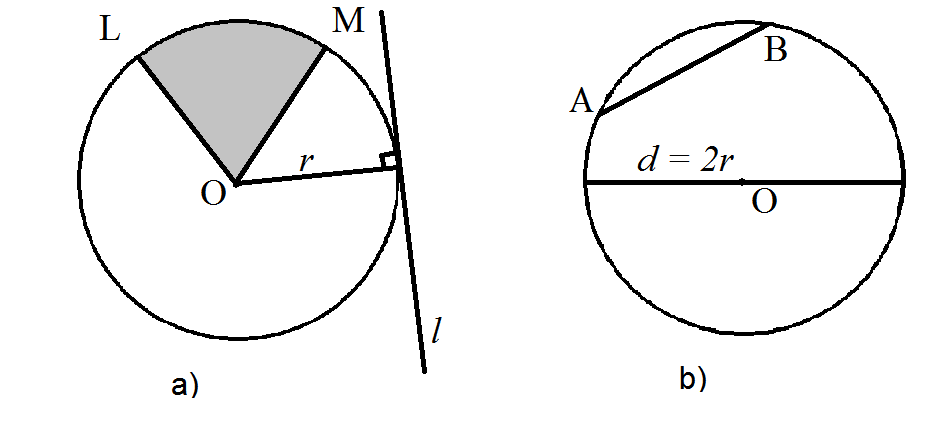
fig.12
Vocabulary
circle [sə:k(ə)l] круг, окружность
plane [plein] плоскость
to lie [lai] лежать
lying [lain] лежащий
distance ['distqns] расстояние
to fix [fiks] фиксировать, закреплять
compass [′kAmpəs] циркуль
perimeter [pə′rimitə(r)] периметр
circumference [sə:′kAmfərəns] окружность
radius [′reidiəs] (pl radii) радиус
space [speis] пространство
sector [′sektə(r)] сектор
across [q'kros] через
to pass [pRs] проходить
diameter [dai′xmitə(r)] диаметр
twice as long as [twais əz lON əz] в два раза длиннее
semi-circle [′semi͵sə:kl] полукруг
to join [GOin] соединять
chord [kLd] хорда
segment [′segmənt] сегмент
to touch [tAC] касаться
tangent [′txnGənt] касательная
contact [′kOntxkt] контакт, точка касания
part [pɑ:t] часть
arc [Rk] дуга
approximate [ə′prOksimət] приблизительный
area ['eəriə] площадь
length [leNT] длина
formula [′fLmjulə] (pl formulae [-li:], formulas) формула
denote [di'nqut] обозначать
Task 1. Answer the questions.
1. What is a circle?
2. What instrument can be used to draw a circle?
3. What is a circumference?
4. What is the name of the distance from the centre of the circle to any point of the circumference?
5. What is a sector?
6. What is the name of the distance right across the circle passing through its centre?
7. What is the length of the diameter equal to?
8. What are the names of two parts of the circle formed by its diameter?
9. What is a chord?
10. What are the names of two parts of the circle formed by a chord?
11. What is a tangent?
12. What is the name of a part of a circumference?
13. What is an approximate value of the number π?
14. What is the circumference of any circle equal to?
15. What is the area of a circle equal to?
Task 2. Draw a circle using a pair of compasses. Denote the centre by a letter.
Task 3. Draw radii, a diameter, a chord, and a tangent in your circle. Denote all the points of contacts with the circumference by letters. Name all the parts of the circle formed by the drawn line segments.
Task 4. Measure the radius of the circle and calculate the length of its circumference and its area using the formulae. Comment your actions.
Task 5. Describe the properties of tangents.
Text 25
SOLIDS (= 3-D SHAPES)
A solid is a three-dimensional figure. Cuboid, cylinder, sphere, pyramid, cone, and prism are examples of solids.
Parts of solids are called: a face – a flat side of solid, an edge – a line where two sides meet, a vertex – a point at a corner where the edges meet.
To find a volume of a cuboid multiply out its length, breadth (= width), and height.
A cube is a kind of cuboid with equal faces, so its volume is one measure cubed.
Prisms can have bases of different shapes, and they are named according to their base, i.e. a triangle prism, a quadrangular prism, pentagonal prism, hexagonal prism, etc. To find the volume of a prism multiply area of its cross-section by the length.
Cylinder is a prism with circular base. Notice: length is replaced by height. Then we have the formula for its volume: πr2h.
A prism is called right if its lateral edges are at right angles to the base (i.e. the lateral faces are rectangles).
Cone is formed by a closed plane curve on a plane (the base) and all the lines joining points of the base to the vertex not in the plane of the base. Cone can be circular or elliptical depending on the base.
Cone like all 3-dimensional figures has an axis of symmetry, it passes from the vertex to the centre. The cone that has its axis perpendicular to its base is a right cone, otherwise the cone is an oblique cone.
Frustum of a cone is formed by removing the top of the cone with a cut parallel to its circular base.
To find the volume of a cone multiply its base area by its perpendicular height and divide by three. The volume of a frustum is difference between the volume of complete cone and volume of cone removed.
Pyramid consists of a base formed by a polygon and a number of triangles (lateral faces) with a common vertex. Pyramids are named according to the base: a triangular pyramid (tetrahedron), a square pyramid, a pentagonal pyramid, etc.
To find the volume of a pyramid multiply its base area by its perpendicular height and divide by three.
To find the volume of a sphere multiply four thirds by π and its radius cubed.
A plane passing through the centre of a sphere cuts it into two hemisphere s.
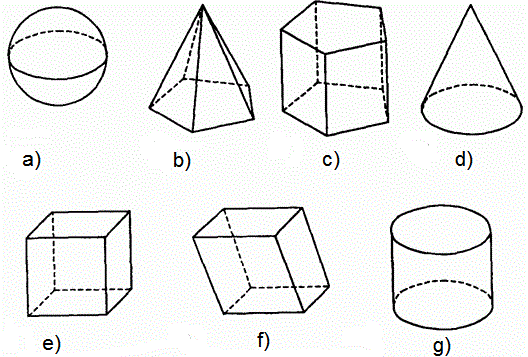
fig.13
Vocabulary
solid [′sOlid] тело (геометрическое), пространственная фигура
three-dimensional [Tri: di′menSn(ə)l] трёхмерный
corner ['kLnq] угол
cuboid [kju′bOid] кубоид
cylinder [′silində(r)] цилиндр
sphere [sfiə(r)] сфера
pyramid [′pirəmid] пирамида
cone [kəun] конус
prism [prizm] призма
face [feis] сторона, грань
flat [flxt] плоский
edge [eG] грань, ребро
volume ['vOljum] объём
length [leNT] длина
vertex [′və:teks] (pl vertices) вершина
cube [kju:b] куб
to measure [′meZə(r)] измерять
To find the volume … чтобы найти объём
triangular [trai′xNgjulə(r)] треугольный
quadrangular [͵kwO′drxNgjulə(r)] четырёхугольный
pentagonal [pen′txgənl] пятиугольный
hexagonal [hek′sxgənl] шестиугольный
cross-section [krOs seS(ə)n] поперечное сечение
circular [′sə:kjulə(r)] круглый
lateral [′lxtər(ə)l] боковой
common ['kOmqn] oбщий
closed curve [kləuzd kə:v] замкнутая кривая
plane [plein] плоскость
elliptical [i′liptik(ə)l] эллиптический
symmetry [′simitri] симметрия
to pass [pRs] проходить
axis [′xksis] (pl axes) ось
otherwise [′ADə͵waiz] иначе, в ином случае
oblique [ə′bli:k] наклонный
frustum [′frAstəm] усечённый
complete [kqm'pli:t] полный, завершённый
according to [q'kLdiN tq] в соответствии
to remove [ri′mu:v] удалить
top [tOp] верх, вершина
cut [kAt] рассекать; срез, сечение
to consist (of) [kən′sist] состоять
tetrahedron [͵tetrə′hidrən, -′hedrən] тетраэдр, четырёхгранник
hemisphere ['hemisfiq] полусфера
Task 1. Answer the questions.
1. What is a solid?
2. What types of solids do you know?
3. What are the names of the parts of solids?
4. What is the volume of a cuboid equal to?
5. What is the property of cube’s size?
6. What does the name of a prism depend on?
7. What kinds of prisms do you know?
8. Which type of prism is called right?
9. What is a cone?
10. Where does an axis of symmetry of cone pass?
11. What types of cones do we know? What does it depend on?
12. How is a frustum of a cone formed?
13. What operations is it necessary to make to find the volume of a cone?
14. What is the volume of a frustum equal to?
15. What is a pyramid consist of?
16. What types of pyramids do we know?
17. What operations is it necessary to make for finding the volume of a pyramid?
Task 2. Complete the sentences.
1. A solid is …
2. A face of a solid is …
3. An edge is …
4. A vertex is …
5. All faces of cube are …
6. The volume of cube is …
7. Bases of prism can be …
8. Depending on their base, prisms are named …
9. A prism is called right if …
10. A base of a cone can be …
11. Axes of symmetry of cone passes …
12. A cone is right if …
13. A cone is oblique if …
14. A frustum of a cone is formed by …
15. A pyramid consists of …
16. Depending on their base, pyramids are named …
Task 3. Identify the solids (= 3D-shapes), name them and their parts.
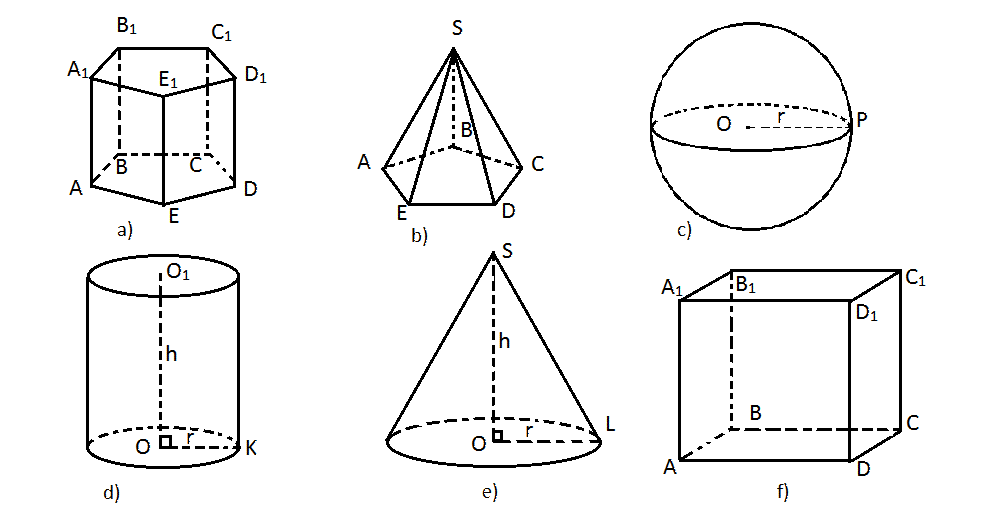
fig.14
Task 4. Make all necessary measurements using a ruler or a compass to find the volume of the solids drawn by you.
Task 5. Translate the sentences into English. Use the information from the text.
1. Вершины пространственной фигуры – это угловые точки, где встречаются её рёбра.
2. Чтобы найти объём кубоида, перемножьте его длину, ширину и высоту.
3. Объём куба равен длине его ребра в третьей степени.
4. Призмы и пирамиды называют по форме их оснований.
5. У прямой призмы боковые грани находятся под углом 900 к основанию.
6. Конус может иметь в основании круг или эллипс.
7. Ось симметрии прямого конуса проходит через центр основания под прямым углом.
8. Основание пирамиды – это многоугольник, а её стороны – треугольники.
9. Сфера может быть поделена на две полусферы плоскостью, проходящей через её центр.
Task 6. Describe the properties of each 3-dimensional (3-D) shapes you know (e.g. cube, cylinder, sphere, hemi-sphere, pyramid, prism, cone).
TEXT 26
TRIGONOMETRY
For finding the length of sides and the sizes of angles in right-angled triangles the laws of trigonometry are used.
There is a definite relationship between sides and angles of a right-angled triangle. The sides of a right-angled ∆ are called hypotenuse and cathetus.
Hypotenuse (= hyp) is the longest side. Cathetus lying directly opposite the angle being used is the opposite side (= opp). Cathetus lying next to this angle is the adjacent (= adj) side.
For example, in the given triangle ABC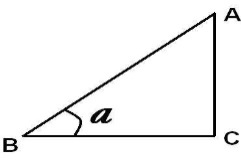 
the angle ‘a’ is used. Then the side AB is a hypotenuse (=hyp), the side AC is the opposite side (= opp), and the side BC is the adjacent side (= adj).
The sine ratio
For any right-angled ∆ the sine of angle ‘a’ (= sin a) equals the length of the opposite side divided by the length of the hypotenuse, i.e. sin a = opp/hyp.
We see that the sine ratio connects the length of the hypotenuse, the size of the angle, and the length of the side opposite the angle. Knowing two of these values we can find the third.
Example 1: We are given: hypotenuse = 10 cm, opposite side = 5 cm. It’s required to work out the sin a.
Solving: By the formula sin a = opp/hyp. Substitute known values - sin a = 5/10 = ½. So, sin a = ½.
Example 2: Work out the length of the opposite side if hypotenuse = 5 cm, sin a = ½.
Solving: By the formula sin a = opp/hyp. Substitute known values – sin 1/2 = opp/5. Then we get: opp = 5 × ½ = 2.5. So, the opposite side is 2.5 cm
The cosine ratio
The cosine ratio connects the length of the hypotenuse, the size of the angle, and the length of the adjacent side. If two of these elements are known, it is easy to find the third.
For any right-angled ∆ cosine of angle ‘a’ (= cos a) equals quotient of dividing the length of adjacent side by the length of hypotenuse, i.e. cos a = adj/hyp.
Example 1: We are given: opposite side equals √11 cm, adjacent side is 5cm. It’s necessary to find cos a.
Solving: First we should calculate the length of hypotenuse. By Pythagorean theorem “the square on the hypotenuse is equal to the sum of the square on the other two sides” we have: hyp2 = opp2 + adj2. Substitute known values and get: hyp = √(11 + 25) = 6. The length of the hypotenuse is 6 cm.
Second. By the formula cos a = adj/hyp. Substitute known values <