A fraction is a quotient of two numbers.
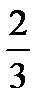 (two thirds) is a fraction. The number ‘2’ (the top number) is called numerator. The number ‘3’ (the bottom number) is called denominator.
(two thirds) is a fraction. The number ‘2’ (the top number) is called numerator. The number ‘3’ (the bottom number) is called denominator.
The fraction where the numerator is less than the denominator is called proper fraction.
The fraction where the numerator is larger than the denominator is called improper or ‘top heavy’ fraction.
The fractions are read as
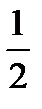 - one second or one (= a) half
- one second or one (= a) half
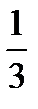 – one third (= a third)
– one third (= a third)
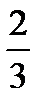 – two thirds
– two thirds
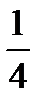 - one (= a) quarter (= one fourth)
- one (= a) quarter (= one fourth)
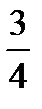 - three quarters (= three fourths)
- three quarters (= three fourths)
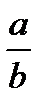 - a over b
- a over b
x + y /2 - x plus y divided by two
- 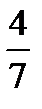 - minus four sevenths.
- minus four sevenths.
Numbers like 2 ¼ (two and a fourth) are called mixed numbers because they are mixture of whole numbers and fractions. They can be written as improper, or ‘top heavy’, fractions. For example: 3 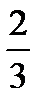 (three and two thirds) =
(three and two thirds) = 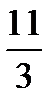 ; 1 ¼ (one and a quarter) =
; 1 ¼ (one and a quarter) = 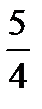 .
.
Fractions can be simplified. To simplify a fraction divide its numerator and denominator by the same number. For example: 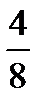 =
= 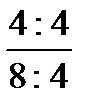 =
= 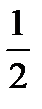 . This is sometimes called canceling a fraction.
. This is sometimes called canceling a fraction.
The fraction is called reducible if its numerator and denominator have a common factor larger than the unit, e.g. 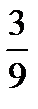 . The number ‘3’ is their common factor.
. The number ‘3’ is their common factor.
The fraction is irreducible if its numerator and denominator have no common factors, e.g. 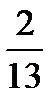 . The numbers ‘2’ and ‘13’ have no common factor.
. The numbers ‘2’ and ‘13’ have no common factor.
Vocabulary
fraction [′frxkS(ə)n] дробь
common fraction [′kOmən ′frxkS(ə)n] простая дробь
vulgar [vAlgq] fraction простая дробь
numerator [nju:mq′reitə(r)] (= top-number) числитель
denominator [di͵nOmi'neitə(r)] (= bottom-number) знаменатель
proper fraction [′prOpə(r)] правильная дробь
improper fraction [im′prOpə(r)] неправильная дробь
‘top-heavy’ fraction [′tOp hevi] неправильная дробь
quarter [′kwOtə(r)] четверть
half [hRf] половина
mixed number [mikst] смешанное число
mixture ['miksCq] соединение, сочетание
inch [inC] дюйм
to simplify [′simplifai] упрощать
cancel(l)ing [′kxnsəliN] сокращение
reducible [ri′dju:s(ə)bl] сократимый
irreducible ["iri′dju:s(ə)bl] несократимый
common factor [′kOmən ′fxktə(r)] общий множитель
e.g. [fər ig′zRmpl] например
These expressions are read:
‘½ mile’ = ‘half a mile’ (= a half mile).
‘¾ hour’ = ‘three quarters of an hour’.
‘1 ½ inches’ = ‘one and a half inches’.
Task 1. Read the fractions. Name the top number and the bottom number in each of them. Give your own examples.
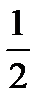 ,
, 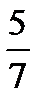 ,
, 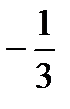 ,
,  ,
, 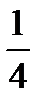 ,
, 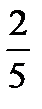 ,
, 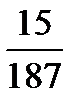 ,
, 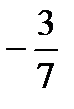 ,
, 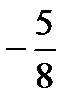 ,
, 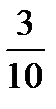 ,
, 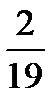 ,
, 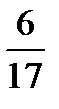 ,
, 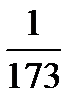 ,
, 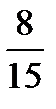 ,
, 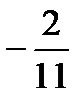 ,
, 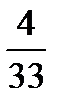 ,
, 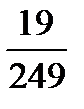 .
.
Task 2. Read the ‘top-heavy’ fractions, change them to mixed numbers. Give your own examples.
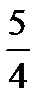 ,
, 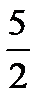 ,
, 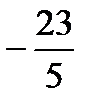 ,
,  ,
, 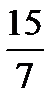 ,
, 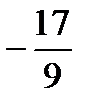 ,
, 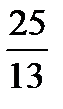 ,
, 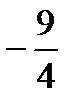 ,
, 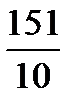 ,
, 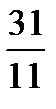 ,
, 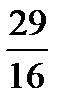 ,
, 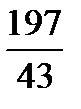 ,
, 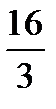 ,
, 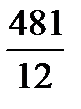 ,
, 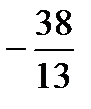 ,
, 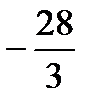 .
.
Task 3. Read the word combinations. Give your own examples.
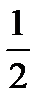 minute,
minute, 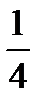 hour,
hour, 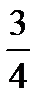 inch,
inch,  volume, 2
volume, 2 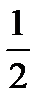 kg, 1
kg, 1 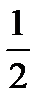 year,
year, 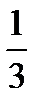 height,
height, 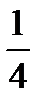 space.
space.
Task 4. Answer the questions.
1. What is a fraction?
2. What’s the name of a top number of a fraction?
3. What’s the name of a bottom number of a fraction?
4. Can we simplify any fraction?
5. Which fraction is proper and which one is improper?
6. What parts have mixed numbers?
Task 5. Simplify the fractions. Comment on your actions. Give your own examples.
Example: 5/10 - Five tenths. This is a proper fraction, the numerator is less than the denominator, and they have a common factor 5. According to the rule we can simplify it dividing both parts by 5. So, we obtain ½ (one second)
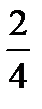 ,
, 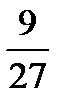 ,
, 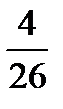 ,
, 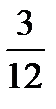 ,
, 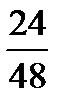 ,
, 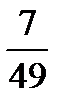 ,
, 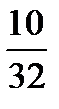 ,
, 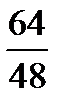 ,
, 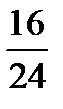 ,
, 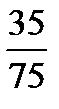 ,
, 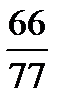 ,
, 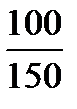 ,
, 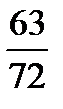 ,
, 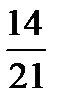 ,
, 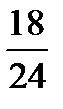 ,
, 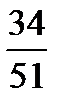 ,
, 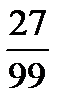 .
.
Text 10
OPERATIONS ON FRACTIONS
a/ Adding fractions
To add two or more fractions find the least common denominator and then add the new numerators keeping the new denominators the same.
For example: 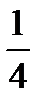 +
+  =
= 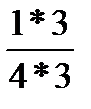 +
+  =
= 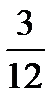 +
+ 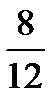 =
= 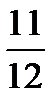
b/ Subtracting fractions
To subtract one fraction from another find the least common denominator and then define the difference between two numerators.
For example: 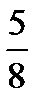 –
– 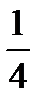 =
= 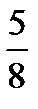 –
– 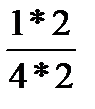 =
= 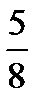 –
– 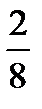 =
= 
c/ Multiplying fractions
To multiply two fractions multiply their numerators and denominators. Simplify, where possible, by canceling.
For example: 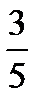 ×
×  =
=  ×
× 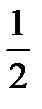 =
= 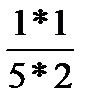 =
= 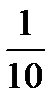
d/ Dividing fractions
To divide two fractions change the division to a multiplication. Remember that to divide by 7, for instance, is the same as to multiply by 1/7, to divide by 3/8 is the same as to multiply by 8/3. Simplify, where possible, by canceling.
For example: 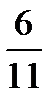 ÷ 4 =
÷ 4 = 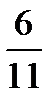 ÷
÷ 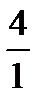 =
= 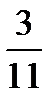 ×
× 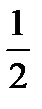 =
= 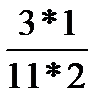 =
= 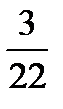 ;
; 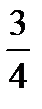 ÷
÷ 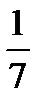 =
= 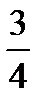 ×
× 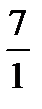 =
= 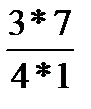 =
= 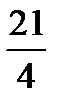 = 5
= 5 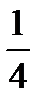
Vocabulary
To add (to multiply, to divide) two fractions … - чтобы сложить (перемножить, разделить) две дроби …
the least common denominator - наименьший общий знаменатель
to keep [ki:p] сохранять
the same [seim] тот же самый
to define [di'fain] определить
to change [CeinG] изменить, поменять
to remember [ri'membq] помнить
for instance [fqr 'instqns] = for example например
possible ['pOsqbl] возможно
Task 1. Work out. Comment on your actions.
a/ 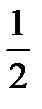 +
+ 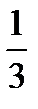 =?
=? 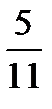 +
+ 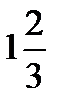 =?
=? 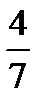 +
+ 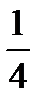 =?
=? 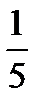 +
+  =?
=? 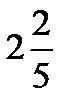 +
+ 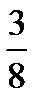 =?
=?  +
+ 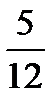 +
+ 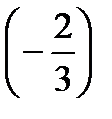 =?
=? 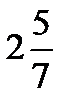 +
+ 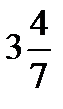 =?
=? 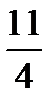 +
+ 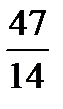 =? 3 +
=? 3 +  +
+ 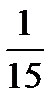 =?
=? 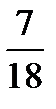 +
+ 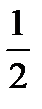 =?
=? 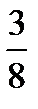 +
+ 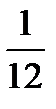 =?
=? 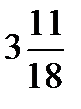 +
+ 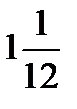 =?
=? 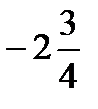 +
+ 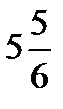 =?
=? 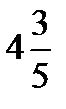 +
+ 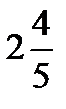 =?
=? 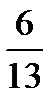 +
+ 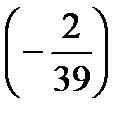 =?
=? 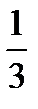 +
+ 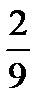 +
+ 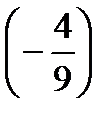 =?
=?
b/  –
–  =?
=? 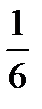 –
– 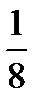 =?
=? 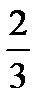 –
– 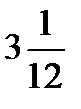 =?
=? 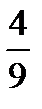 –
– 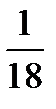 =?
=? 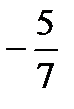 –
– 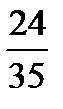 =?
=? 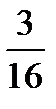 –
– 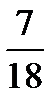 =?
=? 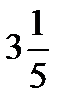 –
– 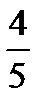 =?
=? 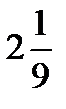 –
– 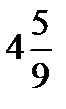 =?
=? 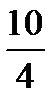 –
–  =?
=? 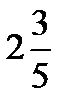 –
– 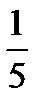 – 1 =?
– 1 =?  –
– 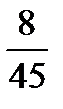 =? 4 –
=? 4 – 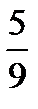 =? 5 –
=? 5 – 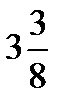 =?
=?
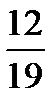 –
– 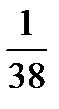 –
– 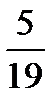 =?
=? 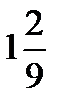 –
– 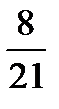 =?
=? 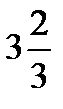 –
– 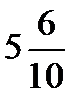 =?
=?
c/ 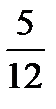 ×
× 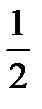 =?
=? 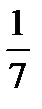 ×
× 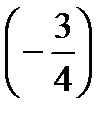 =?
=?  ×
× 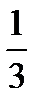 =?
=? 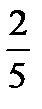 ×
× 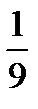 =?
=? 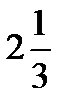 ×
× 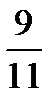 =?
=? 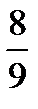 ×
× 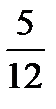 ×
× 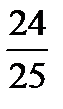 =?
=?
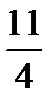 ×
× 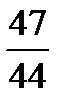 =?
=? 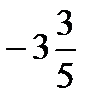 ×
× 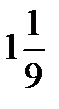 =?
=? 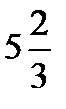 ×
× 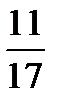 =?
=? 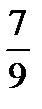 ×
× 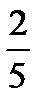 =?
=? 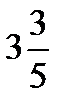 ×
× 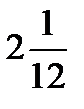 =?
=? 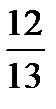 ×
× 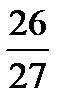 =?
=?
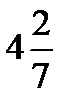 ×
× 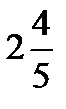 =?
=? 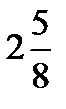 ×
× 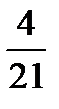 =?
=? 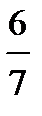 ×
× 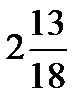 =?
=? 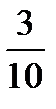 ×
× 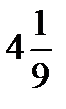 =?
=?
d/ 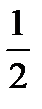 ÷
÷ 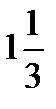 =?
=? 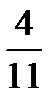 ÷
÷ 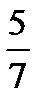 =?
=? 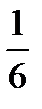 ÷
÷ 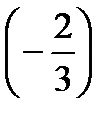 =?
=? 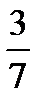 ÷
÷ 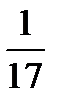 =?
=? 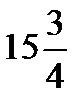 ÷
÷ 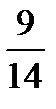 =?
=? 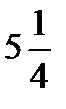 ÷ 7÷
÷ 7÷ 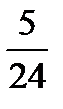 =?
=? 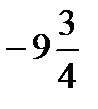 ÷
÷ 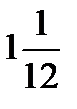 =?
=? 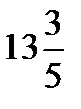 ÷
÷ 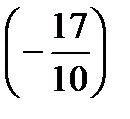 =?
=? 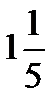 ÷ 12 =?
÷ 12 =? 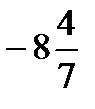 ÷
÷ 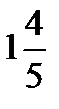 =?
=? 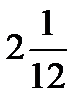 ÷
÷ 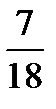 =?
=?
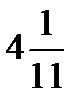 ÷
÷ 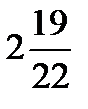 =?
=? 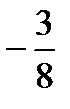 ÷
÷ 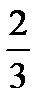 =?
=? 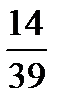 ÷
÷ 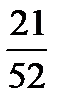 =?
=? 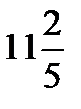 ÷
÷ 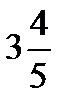 =? 12 ÷
=? 12 ÷ 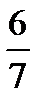 =?
=?
Task 2. Give your own examples of adding, subtracting, multiplying, dividing fractions.
Example 1. 2/3:1/5 =? Two thirds divided by one fifth. By the rule ‘to divide two fractions change division to multiplication’ we have 2/3 * 5/1. Multiplying their numerators and denominators we obtain 2*5/3*1 = 10/3. It’s an improper fraction and it can be written as a mixed number: 3 1/3 (three and one third)
Example 2. 2/3 + 1/5. Two thirds plus one fifth. According to the rule we must find the least common denominator and then add the numerators keeping our new denominator. In our example the least common denominator is 15. So, 2*5/3*5 +1*3/5*3 = 10 + 3/15 = 13/15. This fraction is irreducible, the numbers 13 and 15 have no common fraction.
Task 3. Learn the rules by heart.
Text 11
DECIMALS
PERCENTAGE
The numbers 0.5 (nought point five), 1.24 (one point two four) are decimals. The denominator of decimals is always the multiple of 10, i.e. 10, 100, 1000 etc.
All vulgar (common) fractions can be written as decimals and vice versa. For example: 1/10 is the tenth part of a whole number. It can be written as 0.1 (nought point one), two tenths parts we write as 0.2 (nought point two). The number 1.03 (one point nought three, or one point o [qu] three) is the same as 1 3/100 (one and three hundredths). The number 3.15 is read as ‘three point one five ‘ (= three and fifteen). The number 14.602 is read as ‘fourteen point six nought two’ (= fourteen point six o [qu] two).
To change a common fraction to a decimal divide the numerator by the denominator. For example: 3/5 = 3 ÷ 5 = 0.6.
Some decimals have recurring digits or a set of recurring digits. For example, 1/3 = 0.3333…., 1/7 = 0.142857142857… These are shown by brackets 1/3 = 0.(3), 1/7 = 0.(142857).
“ Per cent ” means ‘out of 100’. 1% (one per cent) of a number is one hundredth part of it, 5% (five per cent) means five hundredths of a number or a quantity.
To change a percentage to a decimal or a fraction divide it by 100, e.g. 25% = 25/100 = ¼. 72% = 72/100 = 0.72.
There is another method of solving this problem. We make up a proportion:
20 = 100%
x = 4% - from which we get 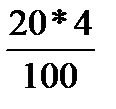 =
= 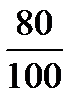 = 0.8
= 0.8
To change a fraction or a decimal to a percentage multiply it by 100, e.g. 1/5 × 100 = 100 ÷ 5 = 20%.
Vocabulary
decimals [′desiməl] десятичные дроби
point [point] точка
multiple [′mAltipl] кратное
i.e. [id′est] (= that is) то есть
etc. [it'setqrq] и так далее, и тому подобное
vice versa [′vaisi′və:sə] наоборот
part [pRt] часть
same [seim] то же самое
To change a common fraction (a percentage, etc.)… – чтобы преобразовать простую дробь (процентное содержание и др.) ….
еxact [ig'zxkt] точный
recurring digits [ri′kAriN ′diGits] период (в периодической дроби)
set множество
bracket [′brxkit] скобка
per cent [pə′sent] процент
percentage [pə′sentiG] процентное содержание
mean [mi:n] (meant, meant) означать
quantity ['kwOntiti] количество
Task 1. Read decimals.
0,34; 1,02; 2,471; 16,184; 14,018; - 0,25; 8,32; 0,005; - 3,502; 49,01; 17,0171; -0,63.
Task 2. Change fractions to decimals. Comment on your actions.
Example: ¾ - According to the rule ‘for changing a vulgar fraction to a decimal divide the numerator by the denominator ‘ we divide 3 by 4 and obtain 0,75 (3: 4 = 0,75).
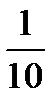 ;
; 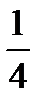 ;
; 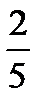 ;
; 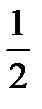 ;
; 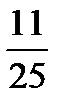 ;
; 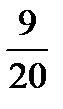 ;
; 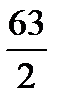 ;
; 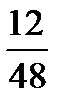 ;
;  ;
; 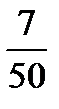 ;
; 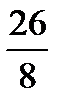 ;
; 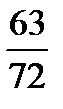 ;
; 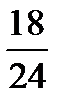 ,
, 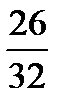 ,
, 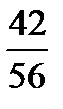 .
.
Task 3. Find a percentage of a number. Follow the pattern. Comment on your actions.
Find 4% of 20. For changing percentage to a decimal we first divide our number 20 by 100 and then multiply the result by 4.
1. 20 ÷ 100 = 0.2
2. 0.2 × 4 = 0.8
So, 4% of 20 is 0.8
5% of 40; 12% of 120; 3% of 18; 15% of 200; 60% of 500; 8% of 50; 26% of 150; 120% of 350; 19,7% of 600; 0,03% of 180; 35% of 255; 48% of 250; 12% of 250; 27% of 700; 3% of 550; 15% of 30; 48% of 460.
TEXT 12
ROUNDING NUMBERS
If we don’t need exact number, it is possible to use rounded or approximate number. Accuracy of rounding depends on our wish to give details.
When the next figure to the right 5 or more round up, e.g. 8.565 ≈ 8.57 or 8.6; 1.78 ≈ 1.8 or 2.
When the next figure to the right less than 5 round down, e.g. 5.21 ≈ 5.2 or 5; 4.32 ≈ 4.3 or 4.
The number can be rounded to the nearest 10 (e.g. 64 ≈ 60), to the nearest 100 (e.g. 326 ≈ 300) etc.
Decimals can be rounded to 2 decimal places (= d.p.), e.g. 3.426 ≈ 3.43; to one decimal place, e.g. 6.27 ≈ 6.3 etc.
There is another kind of rounding when significant figures (= sig.fig.) are used. The most significant figure in a number is the digit with the greatest place value. For instance, in the number 398 the digit 3 has the greatest place value, it is worth 300. So, 3 is the most significant figure.
If we wish to round the number 398 to one significant figure, we get 400 (by the rule about the next digit 5 or more).
Rounding the number 0.00276 to one significant figure we get 0.003. Noughts before the number 2 are not significant, they preserve the place value of the ‘2’.
Vocabulary
to round [raund] округлять
еxact [ig'zxkt] точный
approximate 1/ [ə′prOksimit] приблизительный; 2/ [ə′prOksimeit] приближаться
accuracy [′xkjurəsi] точность
to depend (on) [di'pend] зависеть
detail ['diteil] подробность, деталь
to round up [′raund ′Ap] округлять в сторону увеличения
to round down [′raund ′daun] округлять в сторону уменьшения
nearest ['niqrqst] ближайший
decimal place ['desimql pleis] десятичный знак
kind [kaind] вид
for instance [fqr 'instqns] = for example например
significant [sig′nifikənt] значимый
preserve [pri′zə:v] сохранять
etc. [it'setqrq[ и так далее
by the rule [ru:l] по правилу
Task 1. Round the numbers. Explain your actions. Use information from the text.
a/ 57; 46; 744; 863; 1378; 2453; 537; 348; 29; 2311; 2043; 4019; 208; 342; 264; 599; 2016; 1004.
b/ 0.7; 1.3; 2.42; 1.27; 4.375; 6.187; 1.008; 2.1746; 3.5264; 10.201; 5.13; 2.89; 0.137; 26.07; 24.18; 3.1415; 7.205, 4.188.
Task 2. Give your own examples of rounding numbers.
Text 13
PRIMES