 ,
, 
 ,
, 
 ,
, 
 ,
, 
 ,
, 
 ,
, 
 ,
, 



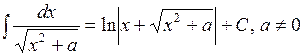
Пример 1. Найти неопределенный интеграл  .
.
►  ■
■
Пример 2. Найти неопределенный интеграл  .
.
► 
 ■
■
Задачи
1 Найти неопределённые интегралы, используя таблицу простейших интегралов. Результат проверить дифференцированием.
1.1  1.6
1.6 
1.2  1.7
1.7 
1.3  1.8
1.8 
1.4  1.9
1.9 
1.5  1.10
1.10 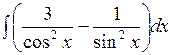
2 Найти неопределенные интегралы, предварительно преобразовав подынтегральную функцию
2.1 а)  б)
б) 
2.2 а)  б)
б) 
2.3 а)  б)
б) 
2.4 a)  б)
б) 
2.5 a)  б)
б) 
2.6 a)  б)
б) 
2.7 a)  б)
б) 
2.8 a)  б)
б) 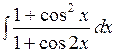
2.9 a)  б)
б) 
2.10 a) 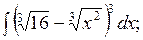 б)
б) 
Тема 2
Метод введения нового аргумента
Необходимые понятия и теоремы
Теорема. Если дана функция  , причем
, причем  имеет первообразную, т. е.
имеет первообразную, т. е. 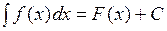 , и если дана функция
, и если дана функция  , причем
, причем  дифференцируема, тогда
дифференцируема, тогда
 или
или  .
.
Пусть 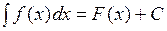 . Возьмем в качестве
. Возьмем в качестве  линейную функцию
линейную функцию  . Тогда
. Тогда  . Отсюда
. Отсюда  .
.
Пример 1. Найти  .
.
► Заметим, что  , тогда
, тогда 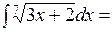


 ■
■
Пример 2. Найти  .
.
► Заметим, что  , тогда
, тогда
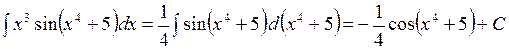 ■
■
Пример 3. Найти  .
.
► Так как  , то
, то
 ■
■
Пример 4. Найти  .
.
► Так как  , то
, то
 ■
■
Пример 5. Найти  .
.
► Так как 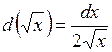 , то
, то
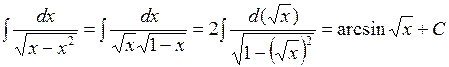 ■
■
Пример 6. Найти  .
.
► 
 ■
■
Пример 7. Найти  .
.
► Выделив полный квадрат в знаменателе, получим
 ■
■
Задачи
1 Найти неопределённые интегралы, применяя метод введения нового аргумента. Результат проверить дифференцированием.
1.1 а)  ; б)
; б)  ; в)
; в) 
1.2 а) 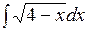 ; б)
; б)  ; в)
; в) 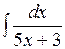
1.3 а)  ; б)
; б)  ; в)
; в) 
1.4 а)  ; б)
; б)  ; в)
; в) 
1.5 а) 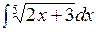 ; б)
; б)  ; в)
; в) 
1.6 а)  ; б)
; б)  ; в)
; в) 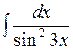
1.7 а) 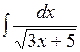 ; б)
; б)  ; в)
; в) 
1.8 а)  ; б)
; б)  ; в)
; в) 
1.9 а)  ; б)
; б) 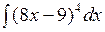 ; в)
; в) 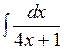
1.10 а)  ; б)
; б)  ; в)
; в) 
2 Найти неопределённые интегралы, применяя метод введения нового аргумента.
2.1 а)  б)
б)  в)
в) 
г)  д)
д) 
2.2 а)  б)
б)  в)
в) 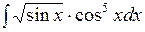 ;
;
г)  ; д)
; д) 
2.3 а)  б)
б)  в)
в) 
г)  д)
д) 


2.4 а) 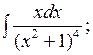 б)
б)  в)
в) 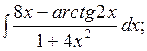
г)  д)
д) 
2.5 а)  б)
б)  в)
в) 
г)  д)
д) 
2.6 а)  б)
б)  в)
в)  ;
;
г) 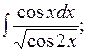 д)
д) 
2.7 а)  б)
б)  в)
в) 
г)  д)
д) 
2.8 а)  б)
б)  в)
в) 
г)  д)
д) 
2.9 a)  б)
б) 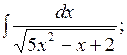 в)
в) 
г)  д)
д) 
2.10 a)  б)
б)  в)
в) 
г)  д)
д) 
Тема 3
Метод интегрирования по частям
Необходимые понятия и теоремы
Теорема. Пусть функции  и
и  имеют непрерывные производные на некотором промежутке. Тогда функция
имеют непрерывные производные на некотором промежутке. Тогда функция  также имеет непрерывную производную на этом промежутке, причем
также имеет непрерывную производную на этом промежутке, причем  . Тогда
. Тогда 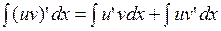 . Отсюда
. Отсюда  или
или  . Отсюда
. Отсюда
 .
.
Последняя формула называется формулой интегрирования по частям.
Пример 1. Найти  .
.
► 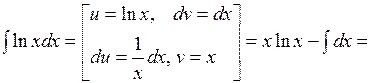
 ■
■
Пример 2. Найти  .
.
►  ■
■
Пример 3. Вычислить возвратный интеграл  .
.
► Обозначим исходный интеграл через  . Тогда
. Тогда


 .
.
Получили уравнение 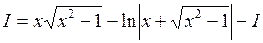 . Решив его относительно
. Решив его относительно  , получим:
, получим:
 ■
■
Задачи
1 Найти интегралы, используя метод интегрирования по частям.
1.1 a) 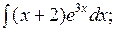 б)
б) 
1.2 a)  б)
б) 
1.3 а)  б)
б) 
1.4 а)  б)
б) 
1.5 а)  б)
б) 
1.6 а) 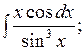 б)
б) 
1.7 а)  б)
б) 
1.8 а)  б)
б) 
1.9 а)  б)
б) 
1.10 а)  б)
б) 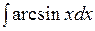
2 Вычислить возвратные интегралы.
2.1  2.6
2.6 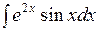
2.2  2.7
2.7 
2.3  2.8
2.8 
2.4  2.9
2.9 
2.5  2.10
2.10 
Тема 4
Интегрирование рациональных функций
Необходимые понятия
В большинстве случаев при интегрировании рациональных функций следует придерживаться следующего алгоритма.
Если дробь  является неправильной (т. е.
является неправильной (т. е.  ), то надо выделить целую часть, разделив числитель на знаменатель. Получим представление
), то надо выделить целую часть, разделив числитель на знаменатель. Получим представление  , где
, где  некоторый многочлен,
некоторый многочлен, 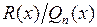 − правильная дробь.
− правильная дробь.
Если дробь  является правильной (т. е.
является правильной (т. е.  ), то многочлен
), то многочлен  необходимо разложить на множители, а затем дробь
необходимо разложить на множители, а затем дробь 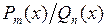 разложить в сумму простейших дробей, т. е.
разложить в сумму простейших дробей, т. е.
дробей вида:
 N,
N,  N,
N,  . (1)
. (1)
Например, дробь  можно представить в виде суммы:
можно представить в виде суммы:

 ,
,
где  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  − некоторые числа, которые можно найти методом неопределенных коэффициентов.
− некоторые числа, которые можно найти методом неопределенных коэффициентов.
Обратимся теперь к интегрированию дробей вида (1).
Если  , то
, то  , а если
, а если  , то
, то
 .
.
Обозначим 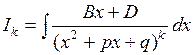 . Для интегрирования такой дроби необходимо выделить в знаменателе полный квадрат:
. Для интегрирования такой дроби необходимо выделить в знаменателе полный квадрат: 
 ,
, 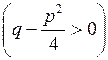 . Далее обозначив
. Далее обозначив  , получим
, получим
 .
.
Теперь 

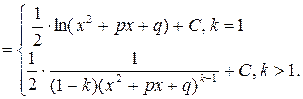
Если  , то
, то  .
.
Если 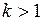 , то для вычисления интегралов
, то для вычисления интегралов  используется рекуррентная формула:
используется рекуррентная формула:
 .
.
Пример. Найти  .
.
► 



 ■
■
Задачи
1 Найти интегралы от рациональных функций, разложив данную функцию в сумму простейших дробей.
1.1 а)  ; б)
; б)  ;
;
в) 
1.2 а)  ; б)
; б)  ;
;
в) 
1.3 а)  ; б)
; б)  ;
;
в) 
1.4 а) 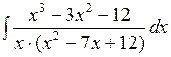 ; б)
; б)  ;
;
в) 
1.5 а)  ; б)
; б)  ;
;
в) 
1.6 а)  ; б)
; б)  ;
;
в) 
1.7 а)  ; б)
; б)  ;
;
в) 
1.8 а)  ; б)
; б)  ;
;
в) 
1.9 а)  ; б)
; б)  ;
;
в) 
1.10 а) 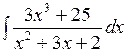 ; б)
; б)  ;
;
в) 
2 Найти интегралы от простейших дробей.
2.1 а)  ; б)
; б) 
2.2 а)  ; б)
; б) 
2.3 а)  ; б)
; б) 
2.4 а)  ; б)
; б) 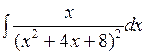
2.5 а) 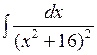 ; б)
; б) 
2.6 а)  ; б)
; б) 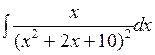
2.7 а)  ; б)
; б) 
2.8 а)  ; б)
; б) 
2.9 а)  ; б)
; б) 
2.10 а)  ; б)
; б) 
Тема 5
Интегрирование некоторых иррациональных функций
Необходимые понятия
Многие интегралы от иррациональных функций удается преобразовать в интегралы от рациональных функций с помощью различных подстановок.
I. Интегралы вида  ,
,
где  Q,
Q,  R,
R,  ,
,  некоторая рациональная функция, сводятся к интегралам от рациональных функций с помощью подстановки:
некоторая рациональная функция, сводятся к интегралам от рациональных функций с помощью подстановки:
 , где
, где  общий знаменатель чисел
общий знаменатель чисел  .
.
II. Интегралы вида  ,
,
где  R,
R,  Q,
Q, 
 называются интегралами от дифференциального бинома. Такие интегралы сводятся к интегралам от рациональных функций подстановками в трех случаях:
называются интегралами от дифференциального бинома. Такие интегралы сводятся к интегралам от рациональных функций подстановками в трех случаях:
1) если  Z, то
Z, то  , где
, где  общий знаменатель чисел
общий знаменатель чисел  и
и 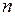 ;
;
2) если  Z, то
Z, то  , где
, где  знаменатель числа
знаменатель числа  ;
;
3) если  Z, то
Z, то  , где
, где  знаменатель числа
знаменатель числа  .
.
III. Интегралы вида
 ,
,  , (*)
, (*)
можно свести к интегралам от рациональных функций с помощью подстановок Эйлера:
1)  , если
, если  ;
;
2)  если
если  ;
;
3)  , где
, где  один из корней квадратного трехчлена
один из корней квадратного трехчлена  .
.
Подстановки Эйлера обычно приводят к громоздким вычислениям. Поэтому для интегралов вида (*) иногда применяют другие методы.
Например, интегралы вида
 , (**)
, (**)
где  многочлен степени n, следует представить в виде:
многочлен степени n, следует представить в виде:
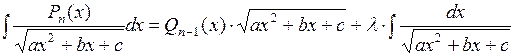 ,
,
где коэффициенты  и
и  находят методом неопределенных коэффициентов (сначала надо продифференцировать обе части последнего равенства, а затем умножить его на
находят методом неопределенных коэффициентов (сначала надо продифференцировать обе части последнего равенства, а затем умножить его на  и приравнять коэффициенты при равных степенях
и приравнять коэффициенты при равных степенях  ).
).
Интегралы  подстановкой
подстановкой 
 сводятся к интегралам вида (**).
сводятся к интегралам вида (**).
Пример 1. Найти  .
.
► 

 ■
■
Пример 2. Найти  .
.
► 
 ■
■
Пример 3. Найти  .
.
► Запишем данный интеграл в виде:  . Вос-пользуемся одной из подстановок для интегралов от дифференциального бинома. В данном случае
. Вос-пользуемся одной из подстановок для интегралов от дифференциального бинома. В данном случае 


 . Найдем
. Найдем  . Получили целое число. Значит, надо использовать третью подстановку:
. Получили целое число. Значит, надо использовать третью подстановку:
 .
.
Теперь  .
.
Далее, применив алгоритм интегрирования рациональных функций, получим 


 где
где  ■
■
Задачи
1 Найти интегралы от иррациональных функций, применив необходимую подстановку.
1.1 а)  б)
б) 
1.2 а)  б)
б) 
1.3 a) 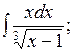 б)
б) 
1.4 a)  б)
б) 
1.5 a)  б)
б) 
1.6 a)  б)
б) 
1.7 a)  б)
б) 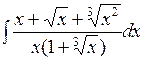
1.8 a)  б)
б) 
1.9 a)  б)
б) 
1.10 a)  б)
б) 
2 Найти интегралы от дифференциальных биномов.
2.1  2.2
2.2 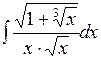 2.3
2.3  2.4
2.4  2.5
2.5  2.6
2.6 
2.7  2.8
2.8  2.9
2.9 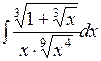
2.10 
3 Найти интегралы, содержащие корень из квадратного трехчлена, используя простейшие методы интегрирования.
3.1 а) 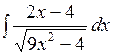 ; б)
; б) 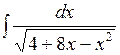 ; в)
; в) 
3.2 а)  ; б)
; б)  ; в)
; в) 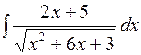
3.3а)  ; б)
; б)  ; в)
; в) 
3.4 а)  ; б)
; б)  ; в)
; в) 
3.5 а)  ; б)
; б) 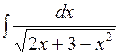 ; в
; в 
3.6 а)  ; б)
; б)  ; в)
; в) 
3.7 а)  ; б)
; б)  ; в)
; в) 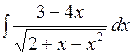
3.8 а)  ; б)
; б)  ; в)
; в) 
3.9 а) 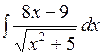 ; б)
; б)  ; в)
; в) 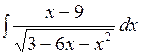
3.10 а)  ; б)
; б)  ; в)
; в) 
4 Найти интегралы, содержащие корень из квадратного трехчлена, используя подстановки Эйлера или другие методы.
4.1  4.6
4.6 
4.2  4.7
4.7 
4.3  4.8
4.8 
4.4  4.9
4.9 
4.5  4.10
4.10 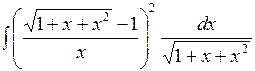
Тема 6