Утверждение 1. Если кривая Г задана уравнением
 ,
,
где  непрерывно-дифференцируемые функции на отрезке
непрерывно-дифференцируемые функции на отрезке 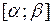 , то длина кривой Г вычисляется по формуле:
, то длина кривой Г вычисляется по формуле:
 .
.
Утверждение 2. Если кривая Г задана уравнением
 ,
,
то ее длина вычисляется по формуле:
 .
.
Утверждение 3. Если кривая Г задана в полярных координатах
 ,
,
то длина кривой вычисляется по формуле:
 .
.
Утверждение 4. Пусть криволинейная трапеция  вращается вокруг оси
вращается вокруг оси  . Объем полученного тела вращения вычисляется по формуле:
. Объем полученного тела вращения вычисляется по формуле:
 .
.
Пусть тело  заключено между плоскостями, перпендикулярными оси
заключено между плоскостями, перпендикулярными оси  и пересекающими эту ось в точках
и пересекающими эту ось в точках  и
и  . Обозначим через
. Обозначим через  фигуру, получаемую в сечении тела
фигуру, получаемую в сечении тела  плоскостью, перпендикулярной оси
плоскостью, перпендикулярной оси  и проходящей через точку
и проходящей через точку  . Пусть при
. Пусть при 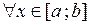 известна площадь
известна площадь  фигуры
фигуры  , причем функция
, причем функция 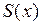 непрерывна на
непрерывна на  .
.
Утверждение 5. При указанных выше условиях объем тела  вычисляется по формуле:
вычисляется по формуле:
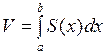 .
.
Пример. Вычислить объем, ограниченный эллипсоидом
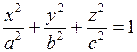 .
.
► Проведем плоскость, перпендикулярную оси  , через точку
, через точку  . В сечении получим эллипс
. В сечении получим эллипс  . Запишем его уравнение в стандартном виде:
. Запишем его уравнение в стандартном виде:
 .
.
Площадь эллипса, получаемого в сечении  . Тогда искомый объем
. Тогда искомый объем 

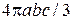 ■
■
Утверждение 6. Если функция  имеет непрерывную производную на
имеет непрерывную производную на  , то площадь поверхности вращения, образованной вращением графика функции
, то площадь поверхности вращения, образованной вращением графика функции 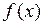 вокруг оси
вокруг оси  , вычисляется по формуле:
, вычисляется по формуле:
 .
.
Если поверхность получена вращением вокруг оси  кривой, заданной параметрически:
кривой, заданной параметрически: 
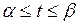 , то
, то
 .
.
Если вокруг оси  вращается кривая, заданная в полярных координатах уравнением
вращается кривая, заданная в полярных координатах уравнением  , то
, то
 .
.
Задачи
1 Вычислить длины дуг кривых, заданных следующими уравнениями.
1.1 а)  ;
;
б) 
1.2 а)  ;
;
б) 

1.3 а)  ;
;
б) 
1.4 а) 
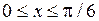 ;
;
б) 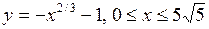
1.5 а) 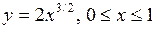 ;
;
б) 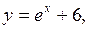

1.6 а)  ;
;
б) 

1.7 а)  ;
;
б) 

1.8 а) 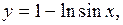
 ;
;
б) 

1.9 а)  ;
;
б) 
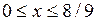
1.10 а)  ;
;
б) 

2 Вычислить длины дуг кривых, заданных параметрически.
2.1 
2.2 
2.3 
2.4 
2.5 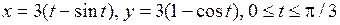
2.6 
2.7 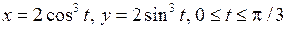
2.8 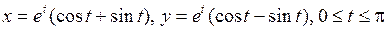
2.9  ,
,  ,
, 
2.10 
3 Вычислить длины дуг кривых, заданных уравнениями в полярных координатах.
3.1 

3.2 

3.3 

3.4 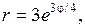

3.5 

3.6 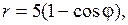

3.7 

3.8 

3.9 

3.10 

4 Вычислить объёмы тел, образованных вращением вокруг оси Ох фигур, ограниченных данными кривыми.
4.1 

4.2 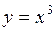 ,
, 
4.3 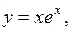
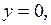

4.4 

4.5 

4.6  ,
, 
4.7 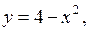

4.8  ,
,  ,
, 
4.9 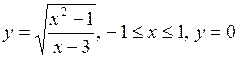
4.10 
5 Вычислить объёмы тел, ограниченных данными поверхностями.
5.1 
5.2 
5.3 
5.4 
5.5 
5.6 
5.7 
5.8 
5.9 
5.10 
6 Вычислить площадь поверхности, образованной вращением данной кривой вокруг оси Ох.
6.1 
6.2 
6.3 
6.4 
6.5 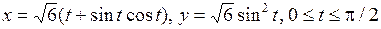
6.6 
6.7 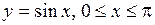
6.8 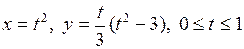
6.9 
6.10 
Тема 6
Несобственные интегралы
Необходимые понятия и теоремы
Определение 1. Пусть функция  интегрируема на отрезке
интегрируема на отрезке 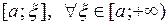 . Несобственным интегралом от функции
. Несобственным интегралом от функции  на промежутке
на промежутке  называется величина
называется величина
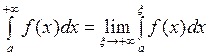 .
.
Если последний предел существует и конечен, то несобственный интеграл называется сходящимся. В противном случае интеграл называется расходящимся.
Определение 2. Пусть функция  определена на конечном промежутке
определена на конечном промежутке  и интегрируема на отрезке
и интегрируема на отрезке  . Несобственным интегралом от функции
. Несобственным интегралом от функции  на промежутке
на промежутке 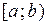 называется величина
называется величина
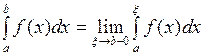 .
.
Пример 1. Исследовать на сходимость 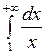 .
.
►  . Следовательно, интеграл расходится ■
. Следовательно, интеграл расходится ■
Пример 2. Исследовать на сходимость  .
.
► 
 .
.
Следовательно, интеграл сходится ■
Пример 3. Используя признаки сравнения,исследовать на сходимость  .
.
► Представим данный интеграл в виде:
 .
.
Так как при 
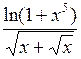
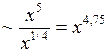 , а интеграл
, а интеграл  сходится, то и интеграл
сходится, то и интеграл  сходится.
сходится.
Так как 
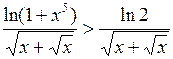 , а при
, а при 

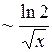 , то из расходимости последнего интеграла следует и расходимость
, то из расходимости последнего интеграла следует и расходимость  . Итак, данный интеграл расходится (как сумма сходящегося и расходящегося интегралов).
. Итак, данный интеграл расходится (как сумма сходящегося и расходящегося интегралов).
Задачи
1 Вычислить несобственные интегралы или установить их расходимость.
1.1 а)  ; б)
; б)  ; в)
; в) 
1.2 а)  ; б)
; б) 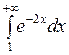 ; в)
; в) 
1.3 а)  б)
б) 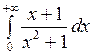 ; в)
; в) 
1.4 а)  ; б)
; б) 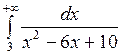 ; в)
; в) 
1.5 а)  ; б)
; б)  ; в)
; в) 
1.6 а)  ; б)
; б) 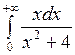 ; в)
; в) 
1.7 а)  ; б)
; б) 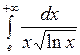 ; в)
; в) 
1.8 а)  ; б)
; б)  ; в)
; в) 
1.9 а)  ; б)
; б)  ; в)
; в) 
1.10 а)  ; б)
; б)  ; в)
; в) 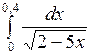
2 Используя признаки сравнения, исследовать на сходимость несобственные интегралы.
2.1 а)  ; б)
; б) 
2.2 а)  ; б)
; б) 

2.3 а) 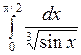 ; б)
; б) 
2.4 а)  ; б)
; б) 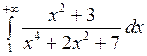
2.5 а)  ; б)
; б) 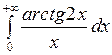
2.6 а)  ; б)
; б) 
2.7 а)  ; б)
; б) 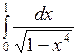
2.8 а) 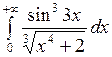 ; б)
; б) 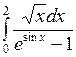
2.9 а) 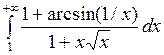 ; б)
; б) 
2.10 а) 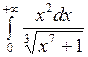 ; б)
; б) 
Литература
1. Тер-Крикоров, А. М. Курс математического анализа: Учеб. пособ. для вузов / А. М. Тер-Крикоров, М. И. Шабунин. − М.: Наука, 1988. − 813 с.
2. Сборник задач по математическому анализу: Интегралы. Ряды: Учеб. пособие для вузов / Л. Д. Кудрявцев [и др.]; Под ред. Л. Д. Кудрявцева. − М.: Наука, 1986. − 528 с.
3. Справочное пособие по математическому анализу. Введение в анализ, производная, интеграл: Учеб. пособие для вузов / И. И. Ляшко [и др.]. − Киев.: «Вища школа», 1984. − 456 с.
4. Сборник индивидуальных заданий по высшей математике: Учеб. пособие. В 3 ч. Ч. 2 / А. П. Рябушко [и др.]; Под общ. ред. А. П. Рябушко. − Мн.: Выш. шк., 1991. − 352 с.
5. Кузнецов, Л. А. Сборник заданий по высшей математике (типовые расчеты): Учеб. пособие для втузов. − М.; Высш. школа, 1983. − 175 с.
Учебное издание