Теорема 1. Если функция  непрерывна на отрезке
непрерывна на отрезке  и если
и если  – какая-нибудь первообразная для функции
– какая-нибудь первообразная для функции  на этом отрезке, то справедлива формула Ньютона-Лейбница:
на этом отрезке, то справедлива формула Ньютона-Лейбница:
 .
.
Теорема 2. Если функции  и
и  имеют на отрезке
имеют на отрезке  непрерывные производные, то справедлива формула интегрирования по частям:
непрерывные производные, то справедлива формула интегрирования по частям:
 .
.
Пример 1. Вычислить интеграл  .
.
► 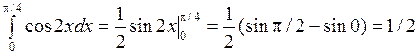 ■
■
Пример 2. Вычислить интеграл  .
.
► 

 ■
■
Задачи
1 Вычислить интегралы с помощью формулы Ньютона-Лейбница.
1.1 а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 
1.2 а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 
1.3 а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 
1.4 а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 
1.5 а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 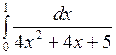
1.6 а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 
1.7 а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 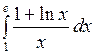
1.8 а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 
1.9 а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 
1.10 а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 
2 Вычислить определенные интегралы.
2.1 а)  ; б)
; б) 
2.2 а)  ; б)
; б) 
2.3 а)  ; б)
; б) 
2.4 а)  ; б)
; б) 
2.5 а)  ; б)
; б) 
2.6 а)  ; б)
; б) 
2.7 а)  ; б)
; б) 
2.8 а) 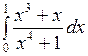 ; б)
; б) 
2.9 а)  ; б)
; б) 
2.10 а) 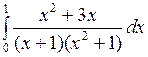 ; б)
; б) 
3 Вычислить интегралы, используя метод интегрирования по частям.
3.1 а)  ; б)
; б) 
3.2 а)  ; б)
; б) 
3.3 а)  ; б)
; б) 
3.4 а)  ; б)
; б) 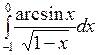
3.5 а)  ; б)
; б) 
3.6 а)  ; б)
; б) 
3.7 а)  ; б)
; б) 
3.8 а) 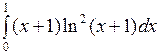 ; б)
; б) 
3.9 а)  ; б)
; б) 
3.10 а)  ; б)
; б) 
Тема 3
Замена переменной в определенном интеграле
Необходимые понятия и теоремы
Теорема. Пусть функция  непрерывна на отрезке
непрерывна на отрезке  , функция
, функция 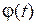 имеет непрерывную производную на интервале
имеет непрерывную производную на интервале  ,
,  отображает отрезок
отображает отрезок  на отрезок
на отрезок  так, что
так, что 
 ,
, 
 . Тогда справедлива формула замены переменной в определенном интеграле:
. Тогда справедлива формула замены переменной в определенном интеграле:
 .
.
Пример 1. Вычислить интеграл  .
.
► 
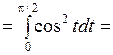
 ■
■
Пример 2. Вычислить интеграл  .
.
► 
 ■
■
Задачи
1 Вычислить интегралы, выполнив необходимую замену переменной.
1.1 а)  ; б)
; б) 
1.2 а)  ; б)
; б) 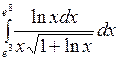
1.3 а)  ; б)
; б) 
1.4 а)  ; б)
; б) 
1.5 а)  ; б)
; б) 
1.6 а)  ; б)
; б) 
1.7 а)  ; б)
; б) 
1.8 а)  ; б)
; б) 
1.9 а)  ; б)
; б) 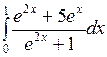
1.10 а)  ; б)
; б) 
2 Вычислить интегралы, используя тригонометрические подстановки.
2.1 а)  ; б)
; б) 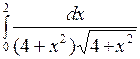
2.2 а)  ; б)
; б) 
2.3 а)  ; б)
; б) 
2.4 а)  ; б)
; б) 
2.5 а)  ; б)
; б) 
2.6 а)  ; б)
; б) 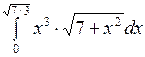
2.7 а)  ; б)
; б) 
2.8 а)  ; б)
; б) 
2.9 а)  ; б)
; б) 
2.10 а)  ; б)
; б) 
3 Вычислить интегралы, используя универсальную тригонометрическую подстановку.
3.1  3.6
3.6 
3.2  3.7
3.7 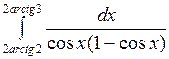
3.3  3.8
3.8 
3.4  3.9
3.9 
3.5  3.10
3.10 
Тема 4
Вычисление площадей с помощью интегралов
Необходимые понятия и теоремы
Утверждение 1. Площадь  криволинейной трапеции (рисунок 1) вычисляется по формуле:
криволинейной трапеции (рисунок 1) вычисляется по формуле:
 .
.

Рисунок 1 − Криволинейная трапеция
Рассмотрим фигуру  , ограниченную отрезками прямых
, ограниченную отрезками прямых  и графиками непрерывных функций
и графиками непрерывных функций  и
и  , где
, где  при
при  (рисунок 2).
(рисунок 2).
Утверждение 2. Площадь фигуры  (рисунок 2) вычисляется по формуле:
(рисунок 2) вычисляется по формуле:
 .
.

Рисунок 2 − Фигура 
Утверждение 3. Площадь криволинейного сектора (рисунок 3) вычисляется по формуле:
 .
.

Рисунок 3 − Криволинейный сектор
Задачи
1 Вычислить площадь фигур, ограниченных графиками данных функций.
1.1 а) 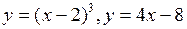 ;
;
б) 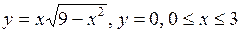
1.2 а) 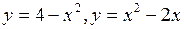 ;
;
б) 
1.3 а)  ;
;
б) 
1.4 а)  ;
;
б) 
1.5 а)  ;
;
б) 
1.6 а)  ;
;
б) 
1.7 а)  ;
;
б) 
1.8 а)  ;
;
б) 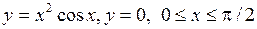
1.9 а)  ;
;
б) 
1.10 а)  ;
;
б) 
2 Решить задачу.
2.1 Вычислить площадь фигуры, ограниченной осью абсцисс и линиями  и
и  .
.
2.2 Вычислить площадь фигуры, ограниченной линиями  и
и  .
.
2.3 Найти площадь фигуры, ограниченной графиком функции  , и отрезком оси абсцисс, соединяющим две последовательные точки пересечения этого графика с осью абсцисс.
, и отрезком оси абсцисс, соединяющим две последовательные точки пересечения этого графика с осью абсцисс.
2.4 Вычислить площадь фигуры, ограниченной линиями  и
и  .
.
2.5 Вычислить площадь фигуры, ограниченной линией  , осью ординат и прямыми
, осью ординат и прямыми  и
и  .
.
2.6 Вычислить площадь криволинейной трапеции, ограниченной линией  и осью абсцисс.
и осью абсцисс.
2.7 Найти площадь фигуры, ограниченной замкнутой линией  .
.
2.8 Круг  разделен параболой
разделен параболой  на две части. Найти площадь меньшей части.
на две части. Найти площадь меньшей части.
2.9 Парабола  делит круг
делит круг  на две части. Найти площадь меньшей части.
на две части. Найти площадь меньшей части.
2.10 Вычислить площади фигур, образованных пересечением эллипса  и гиперболы
и гиперболы 
3 Вычислить площади фигур, ограниченных линиями, заданны-ми уравнениями в полярных координатах. Сделать чертёж.
3.1 а)  ;
;
б)  ,
, 
3.2 а)  ;
;
б)  ,
, 
3.3 а) 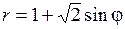 ;
;
б)  ,
, 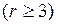
3.4 а)  ;
;
б) 
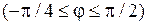
3.5 а)  ;
;
б)  ,
, 
3.6 а)  ;
;
б) 

3.7 а)  ;
;
б)  ,
, 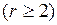
3.8 а)  ;
;
б) 
3.9 а)  ;
;
б)  ,
, 
3.10 а)  ;
;
б)  ,
, 
Тема 5
Вычисление длин кривых, объемов, площадей поверхностей