Необходимые понятия
Интеграл вида  , где
, где  некоторая рациональная функция переменных
некоторая рациональная функция переменных  и
и  , можно свести к интегралу от рациональной функций с помощью подстановки:
, можно свести к интегралу от рациональной функций с помощью подстановки:
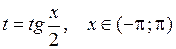 .
.
Тогда  .
.
Эта подстановка называется универсальной тригонометрической подстановкой.
Поскольку универсальная тригонометрическая подстановка часто приводит к громоздким вычислениям, то в частных случаях удобнее пользоваться следующими подстановками:
если  , то
, то  ;
;
если 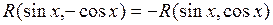 , то
, то  ;
;
если 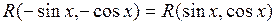 , то
, то  или
или 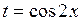 .
.
Пример 1. Найти  .
.
► 
 ■
■
Пример 2. Найти  .
.
► 
 , где
, где  ■
■
Задачи
1 Найти интегралы от тригонометрических функций, выполнив необходимое преобразование подынтегрального выражения.
1.1 a)  ; б)
; б) 
1.2 а)  ; б)
; б) 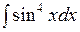
1.3 а)  ; б)
; б) 
1.4 а)  ; б)
; б) 
1.5 а)  ; б)
; б) 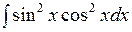
1.6 а) 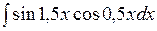 ; б)
; б) 
1.7 а)  ; б)
; б) 
1.8 а)  ; б)
; б) 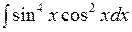
1.9 а)  ; б)
; б) 
1.10 а)  ; б)
; б) 
2 Найти интегралы от тригонометрических функций, выбрав необходимую подстановку.
2.1 а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 
2.2 а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 
2.3 а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 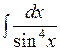
2.4 а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 
2.5 а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 
2.6 а) 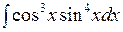 ; б)
; б)  ; в)
; в) 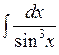 ; г)
; г) 
2.7 а)  ; б)
; б) 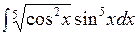 ; в)
; в)  ; г)
; г) 
2.8 а) 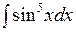 ; б)
; б) 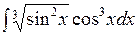 ; в)
; в)  ; г)
; г) 
2.9 а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 
2.10 а)  ; б)
; б)  ; в)
; в) 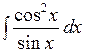 ; г)
; г) 
3 Найти данные интегралы с помощью универсальной тригонометрической подстановки.
3.1 а) 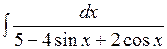 ; б)
; б) 
3.2 а) 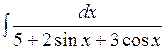 ; б)
; б) 
3.3 а)  ; б)
; б) 
3.4 а) 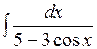 ; б)
; б) 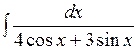
3.5 а)  ; б)
; б) 
3.6 а)  ; б)
; б) 
3.7 а)  ; б)
; б) 
3.8 а)  ; б)
; б) 
3.9 а)  ; б)
; б) 
3.10 а)  ; б)
; б) 
Определенные интегралы
Тема 1
Определение интеграла Римана
Необходимые понятия и определения
Пусть функция  определена на отрезке
определена на отрезке  . Разбиением Т отрезка
. Разбиением Т отрезка 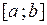 называется множество точек
называется множество точек 
 , таких, что
, таких, что  .
.
Обозначим  – i-тый частичный отрезок разбиения,
– i-тый частичный отрезок разбиения,  – длину этого отрезка.
– длину этого отрезка.
Величину 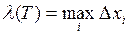 назовем мелкостью разбиения Т. Возьмем на каждом отрезке разбиения произвольную точку
назовем мелкостью разбиения Т. Возьмем на каждом отрезке разбиения произвольную точку  . Получим разбиение с отмеченными точками.
. Получим разбиение с отмеченными точками.
Сумма  называется интегральной суммой для функции
называется интегральной суммой для функции  при заданном разбиении Т и фиксированных отмеченных точках
при заданном разбиении Т и фиксированных отмеченных точках  .
.
Определение. Число I называется определенным интегралом от функции 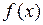 по отрезку
по отрезку 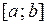 , если для
, если для  такое, что для любого разбиения Т, мелкость которого
такое, что для любого разбиения Т, мелкость которого  меньше
меньше  , и при любом выборе отмеченных точек
, и при любом выборе отмеченных точек  выполняется неравенство:
выполняется неравенство:
 .
.
Обозначается определенный интеграл  .
.
Данное определение интеграла означает, что число I является пределом интегральных сумм  при мелкости разбиения
при мелкости разбиения  , стремящейся к нулю, т. е.
, стремящейся к нулю, т. е.  , причем этот предел не зависит от выбора отмеченных точек
, причем этот предел не зависит от выбора отмеченных точек 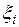 .
.
Если для функции  существует число I, то функцию
существует число I, то функцию  называют интегрируемой (по Риману) на отрезке
называют интегрируемой (по Риману) на отрезке  , и говорят, что существует интеграл от функции
, и говорят, что существует интеграл от функции  на отрезке
на отрезке 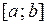 .
.
Пример. Вычислить интеграл  как предел интегральных сумм, разбивая отрезок интегрирования на n равных частей и выбирая отмеченные точки
как предел интегральных сумм, разбивая отрезок интегрирования на n равных частей и выбирая отмеченные точки  в серединах отрезков интегрирования.
в серединах отрезков интегрирования.
► Так как длина отрезка интегрирования равна 7, то  .
.
Тогда  .
.
Найдем координаты середин отрезков разбиения:
 .
.
Составим интегральную сумму и вычислим её:


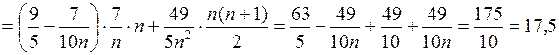 .
.
Заметим, что подынтегральная функция является интегрируемой (как непрерывная функция), а значит, величина интеграла не зависит ни от способа разбиения отрезка интегрирования, ни от выбора отмеченных точек. Значит,  ■
■
Задачи
1 Вычислить интеграл  как предел интегральных сумм, разбивая отрезок
как предел интегральных сумм, разбивая отрезок  на n равных частей и выбирая точки
на n равных частей и выбирая точки  в серединах отрезков разбиения.
в серединах отрезков разбиения.
1.1 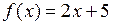 ,
, 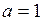 ,
, 
1.2 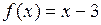 ,
,  ,
, 
1.3  ,
,  ,
, 
1.4  ,
,  ,
, 
1.5  ,
,  ,
, 
1.6  ,
,  ,
, 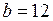
1.7  ,
, 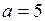 ,
, 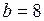
1.8  ,
,  ,
, 
1.9  ,
, 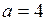 ,
, 
1.10 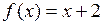 ,
,  ,
, 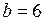
2 Вычислить интеграл  как предел интегральных сумм, выбирая точки разбиения так, чтобы их координаты образовывали геометрическую прогрессию.
как предел интегральных сумм, выбирая точки разбиения так, чтобы их координаты образовывали геометрическую прогрессию.
2.1  ,
, 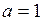 ,
, 
2.2  ,
, 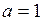 ,
, 
2.3  ,
,  ,
, 
2.4  ,
,  ,
, 
2.5 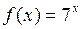 ,
, 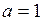 ,
, 
2.6  ,
,  ,
, 
2.7  ,
,  ,
, 
2.8 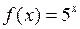 ,
,  ,
, 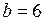
2.9  ,
,  ,
, 
2.10  ,
,  ,
, 
Тема 2
Формула Ньютона-Лейбница