Для анализа производства в краткосрочном периоде рассмотрим краткосрочную функцию производства, предполагающую наличие у фирмы частично постоянных и частично переменных ресурсов:
где 
— количество постоянного ресурса;
L — количество переменного ресурса
| ! |
Для упрощения анализа предположим, что фирма использует всего два ресурса: переменный ресурс — труд L и постоянный ресурс - капитал К.. А также введем новые понятия: совокупный, средний и предельный продукты:
• совокупный продукт (total, product. TP) — общий объем произведенных фирмой товаров и услуг за единицу времени,
• средний продукт (average, product. AP) — доля совокупного продукта на единицу используемою ресурса.
Различают средний продукт по переменному ресурсу -
и средний продукт по постоянному фактору — АРК = ТР/К;
♦ предельный продукт (marginal product, МР) — величина прироста совокупного продукта при изменении используемого ресурса на единицу.
Поскольку рассматривается краткосрочный период, изменяться может лишь переменный ресурс, в нашем случае — труд.
♦ Предельный продукт труда, МРL показывает прирост совокупного продукта при увеличении количества труда на единицу и подсчитывается по одной из двух возможных формул:
1) дискретный предельный продукт:
где 
- два последующих значения совокупного продукта (объема выпуска);
— соответственно два последовательных значения переменного ресурса (труд).
Формула дискретного предельною продукта используется в том случае, когда имеются только количественные значения выработки и используемых ресурсов в единицу времени, но неизвестна производственная функция.
|
|
Если же производственная функция известна, то может быть использована другая формула:
2) непрерывный предельный продукт
MPL = dQ/dL= Q'(L)'.
Далее на условном примере рассмотрим способ расчета базовых производственных показателей.
Для заданного количества оборудования (K = const) наем различного числа работников позволяем фирме подучить следующие показатели производительности труда (табл. 5.1).
1 Если вПроизводстве несколько переменных ресурсов, то нахождение предельного о продукта одного из них осуществляется с помощью частных производных (см. Математическое приложение).
Пусть производственная функция имеет вид 
, где X, Z -переменные ресурсы
Тогда предельные продукты ресурсов составят соответственно 
, a 
.
Таблица 5.1
Расчет среднего и предельного продуктов труда
|
| Объем |
Представим полученные результаты графически (рис. 5.1). Как видим, производственный процесс, отраженный в производственной функции, последовательно проходит три этапа.
| Рис 9.1. Продукты труда а)совокупный б) средний и предельный |
Первый эman — этап возрастающей отдачи (при L от 0 до 3 работников). Происходит ускоренный рост совокупного объема выпуска. Повышается средняя производительность труда А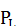 
/. предельный продута труда М 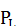/ также увеличивается и достигает своего максимального значения (в нашей задаче М 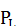= max при L=3 чел.).
|
|
Второй этап — этап убывающей отдачи (при L от 3 до 7 чел.). При продолжающемся росте объема выпуска наблюдается постепенное сокращение предельной M 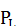производительности труда до нулевого уровня (М 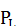/, в 0 при L = 7). В этих условиях совокупный объем производства ТР становится максимально возможным, и его дальнейшее увеличение за счет прироста только переменных ресурсов уже неосуществимо.
Третий этап — этап отрицательной отдачи (при L от 8 чел. и более). Наблюдается сокращение объемов выпуска. а предельный продукт приобретает отрицательное значение (М 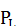/ < 0). Использование дополнительных трудовых ресурсов становится экономически неоправданным.
Очевидно, что для достижения наиболее эффективных результатов и минимизации издержек фирме следует использовать переменный ресурс в объеме, соответствующем второму лапу.
На первом этапе производства дополнительное использование переменного ресурса ведет к снижению средних издержек и росту прибыли предприятия.
На третьем этане краткосрочного периода использование переменных ресурсов сверх разумных норм сокращает совокупный объем выпуска, при этом средние издержки растут, а прибыльность падает.
| ! |
Причина подобного поведения производственной функции кроется в законе убывающей отдачи.
Начиная с некоторого момента времени дополнительное использование переменного ресурса при неизменном количестве постоянного ресурса ведет к сокращению его предельной отдачи, или предельного продукта.
|
|
Этот закон носит универсальный характер и присущ практически всем экономическим процессам.
Рассмотрим пример 5.2.