Долгосрочный период производства: изокоста и изокванта

В долгосрочном периоде все факторы производства являются переменными. В зависимости от состояния рыночного спроса, а также от цен на экономические ресурсы фирма может выбрать любой из технологически эффективных вариантов производства.

Для того чтобы определить, какая из доступных технологий будет экономически эффективной, воспользуемся моделью изо­кванты и изокосты.

Возможные варианты производства различных объемов вы­пуска представлены в табл. 5.2. Для простоты анализа предполо­жим использование не более 6 единиц труда L и 4 единиц обору­дования К..

Как видно из представленной табл. 5.2, существует несколь­ко комбинаций труда и капитала, обеспечивающих в опреде­ленных пределах заданный объем выпуска. Например, объем Q = 25 ед. можно получить, используя 1 ед. труда и 2 ед. капита­ла или 2 ед. труда и 1 ед. капитала (в таблице выделено шриф­том). Аналогичным образом Q = 61 ед. можно получить, ис­пользуя комбинации (6,2). (4.3) и (3,4).

Если отложить по горизонтальной оси количество единиц труда, но вертикальной — количество единиц каптала, затем обозначить точки, в которых фирма выпускает один и тот же объем, то получится линия изокванты (IQ, "изо" — равный, "кванта" - количество) (рис. 5.2).

Изоквантa показывает совокупность всех комбинаций факторов произ­водства, обеспечивающих заданный объем выпуска.

Набор изоквант, характеризующий данную производственную функцию, называется картой изоквант'.

Угол наклона линии иэокванты характеризуется коэффици­ентом предельной нормы технологического смещения.

'Свойства стандартных изоквант, описывающих технологию производства аналогичны характеристикам кривых безразличия, описывающих потребительские предпочтения:

1)изокванта, так же как и кривая безразличия, является непрерывной функцией, а не набором дискретных точек;

2)для любого заданного объема выпуска может быть проведена своя изокванта, отражающая различные комбинации экономических ресурсов, обеспечивающих производителю одинаковый объем производства;

3)изокванты, описывающие данную производственную функцию, никогда не пересекаются;

4) изокванты не имеют участков возрастания.

Предельная норна технологического замещения {Marginal Rate of Technical Substitution, MRTS)I одного ресурса на другой (например, труда на капитал) показывает, сколько единиц труда необходимо для заме­щения одной единицы капитала, чтобы o6ъем выпуска не изменился.

Оцепить норму замещения можно отношением прироста од­ного ресурса к приросту другого ресурса (см. пример 5.1) или производной функцией производства (см. задачу 5.1) но формуле:

MRTS - dK/dL - K'(L).

В силу отрицательною наклона кривой безразличия данное отношение всегда величина отрицательная. Однако в большинстве случаев минусом пренебрегают, ибо основное значение имеет абсолютная величина коэффициента.

Капитал К

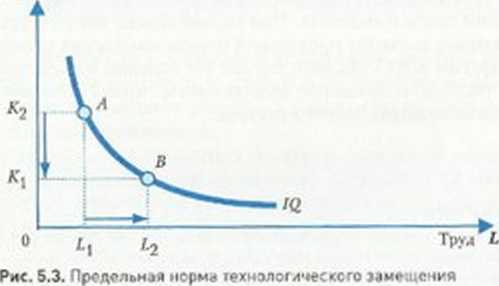
Как видно на рис. 5.3, при переходе из точки А в точку В объем производства остается неизменным. Это означает, что сокращение выпуска в результате уменьшения затрат капитала (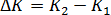) компенсируется увеличением выпуска за счет ис­пользования дополнительного количества труда (L=L₂.- )

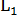Используем приведенный материал для решения задачи 5.2.

Задача 5.2

Похождение MRTS для заданной функции

Пусть технология некоторого производственного процесса задана функци­ей Q=10KL. На производстве занято 5 чел. Требуется оценить норму заме­щения одного работника дополнительным количеством оборудования так, чтобы объем выпуска сохранился на уровне Q = 500 ед. продукции в день.

Решение

500 - 10KL;

К = 50/L= 50L^-2

MRST=K'(L)=-50L^-2=-50/L²

При L = 5 предельная норма технологического замещения труда капиталом MRTS = -50/5² =-2

! Экономический смысл полученного коэффициента: для сохранения объ­ема производства на неизменном уровне сокращение числа занятых на единицу продукции должно быть компенсировано увеличением объема ис­пользованного оборудования на 2 единицы.

В большинстве случаев норма замещения меняется при дви­жении вдоль изокванты. При перемещении вниз по кривой аб­солютное значение предельной нормы замещения одного ресур­са другим MRST убывает, так как все большее количество перво­го ресурса приходится использовать, чтобы компенсировать снижение затрат второго ресурса.

Задача 5.2

(Продолжение)

Если фирм.1 последовательно увеличивает число занятых на производстве работников, то это сопровождается сокращением абсолютной величины предельной нормы замещения:

при L = 6 чел. MRTS =-50/36 = -1,39;

при L = 7 чел. МRTS =-50/49 =-1,02;

...

при L = 10 чел. MRTS=-50/100 = -0.5

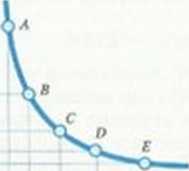
В дальнейшем MRTS достигает своего предела (MRTS = 0), а изокванта приобретает горизонтальный вид (это изображено на рис. 5.4).

Очевидно, что дальнейшее снижение затрат капитала приведет лишь к сокращению объемов выпуска. Количество капитала и точ­ке Е — минимально допустимое для данного объема производства (аналогичным образом минимально допустимое для производства данного объема количество труда имеет место в точке А).

Убывание предельной нормы замещения одного ресурса дру­гим характерно для большинства технологических процессов, описываемых изоквантами стандартного вида..

Капитал К

Рис. 5.4. Убывание предельной нормы технологического замещения

Однако при выборе оптимальной комбинации ресурсов про­изводитель должен учитывать не только доступную ему техноло­гию, но и свои финансовые ресурсы, а также цены на соответст­вующие факторы производства.

Совокупность двух последних факторов определяет область доступных производителю экономических ресурсов.

Бюджетное ограничение производителя может быть записа­но в виде неравенства

Р_кК + P _LL < TC,

Где P_K, , P _L - цена капитала и труда;

K, L — количество капитала и труда;

ТС (total cost) — совокупные расходы (издержки) фирмы на приоб­ретение ресурсов

Если производитель полностью расходует свои средства на приобретение данных ресурсов, то это отражается равенством

Р_кК + P _LL - ТС

или

К.™-Ill ^К г* Р*

Полученное уравнение называют уравнением изокосты.

Линия изокосты (рис. 5.5) содержит набор комбинаций экономических ре­сурсов, которые фирма может приобрести с учетом рыночных цен на ресур­сы и при полном использовании своего бюджета.

Наклон линии изокосты определяется отношением рыноч­ных цен на труд и на капитал (-P _L/P _K), что вытекает из уравне­ния изокосты.

Стремление фирмы к эффективному производству побужда­ет ее к достижению максимально возможной выработки при за­данных затратах на ресурсы или, что то же самое, к минимиза­ции издержек при производстве заданного объема выпуска.

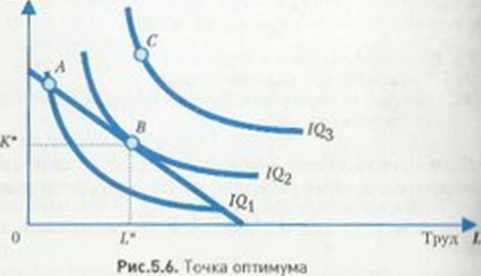
Оптимальная комбинация ресурсов, обеспечивающая минимальный уровень совокупных издержек, лежит в точке каса­ния линий изокосты и изокванты (рис. 5.6).

Капитал К

Оптимальная комбинация ресурсов предполагает выполнение двух условий.

Во-первых, полное использование средств, предназначенных для покупки ресурсов, а во-вторых, такое распределение расходов между ресурсами, при котором предельная норма технологиче