Проверка независимости значений уровней случайной компоненты осуществляется для выявления существующей автокорреляции остаточной последовательности. Эта проверка может производиться по ряду критериев.
Наиболее распространенным является d-критерий Дарбина - Уотсона. Расчетное значение этого критерия находится по формуле:
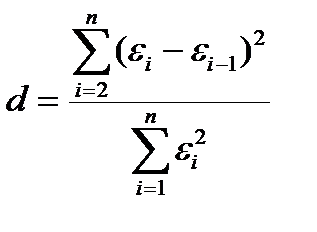
Расчетное значение d-критерия в интервале от 2 до 4 свидетельствует об отрицательной связи. В этом случае его надо преобразовать по формуле:
d' = 4 – d
и в дальнейшем использовать значение d' Расчетное значение критерия d или d' сравнивается с верхним d2 и нижним d1 критическими значениями статистики Дарбина - Уотсона.
Для 5%-го уровня значимости эти значения для ряда количества определяемых параметров р приведены в таблице:
Таблица №10
| n | p=1 | p=2 | p=3 | |||
| d1 | d2 | d1 | d2 | d1 | d2 | |
| 1,08 | 1,36 | 0,95 | 1,54 | 0,82 | 1,75 | |
| 1,20 | 1,41 | 1,10 | 1,54 | 1,00 | 1,68 | |
| 1,35 | 1,49 | 1,28 | 1,57 | 1,21 | 1,65 |
Если расчетное значение критерия d больше верхнего табличного значения d2, то гипотеза о независимости уровней остаточной последовательности, то есть об отсутствии в ней автокорреляции принимается.
Если расчетное значение d меньше нижнего табличного d1 то эта гипотеза отвергается и модель считается неадекватной.
Если значение d находится между значениями d1 и d2, включая сами эти значения, то считается, что нет достаточных оснований делать тот или иной вывод и необходимы дальнейшие исследования, например по большему числу наблюдений.
Вывод об адекватности модели делается, если все 4 проверки свойств остаточной последовательности дают положительный результат. Для адекватных моделей имеет смысл ставить задачу оценки их точности.
В данной задаче:
d = 2,77 - критерий Дарбина -Уотсона
Расчетное значение d-критерия свидетельствует об отрицательной связи.
d' = 1,23 и d1= 1,00, d2=l,68
Так как расчетное значение критерия d находится между значениями d1 и d2, то в этом случае нужно проводить дополнительные исследования.
Определение точности модели
В качестве критерия точности мы принимаем степень совпадения теоретических значений у с практическими значениями у.
Показатели точности построены на сопоставлении теоретических значений с практическими.
Показатели:
1. Среднеквадратичное отклонение:
где i = 1 ÷ n
yi - фактическое значение рядя
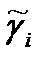- теоретическое значение ряда
n - количество наблюдений
р - количество независимых параметров
Недостаток этого показателя: он зависит от масштаба y.
2.Средняя относительная ошибка аппроксимации:
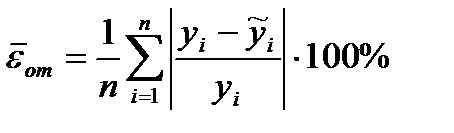
3. Коэффициент сходимости:
где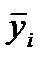 
- среднее значение ряда.
Показывает, какая доля изменения результирующего признака может быть объяснена изменением невключенных в модель факторов.
4. Коэффициент детерминации:
В данной задаче: σ = 0,91
= 0,09%
φ2= 0,05
R2= 0,95
На основании указанных показателей можно сделать выбор из нескольких адекватных трендовых моделей экономической динамики наиболее точной, хотя может встретиться случай, когда по некоторому показателю более точна одна модель, а по другому – другая модель.