Статистика уровня жизни населения. Основные индикаторы уровня жизни населения. Индекс развития человеческого потенциала (ИРЧП)
Уровень жизни определяется, прежде всего, как обеспеченность населения необходимыми материальными благами и услугами, достаточным уровнем их потребления и степенью удовлетворения разумных (рациональных) потребностей. Материальные блага – это продукты питания, одежда, обувь, предметы культуры и быта, жилище. Услуги – это полезные результаты деятельности, которые либо не имеют материального воплощения (непроизводственные услуги – результаты деятельности медицинских учреждений, учётных заведений, учреждений культуры и искусства, жилищно-коммунальные услуги, услуги пассажирского транспорта и др.), либо имеют (производственные услуги – услуги различных ателье по пошиву и ремонту одежды и обуви, мастерских по ремонту бытовой техники, химчисток, прачечных, пунктов проката и т.д.).
Денежная оценка благ и услуг, фактически потребляемых в домохозяйстве в течение известного промежутка времени, представляет собой стоимость жизни.
Можно выделить четыре уровня жизни населения:
1) достаток (пользование благами, обеспечивающими всестороннее развитие человека);
2) нормальный уровень (рациональное потребление по обоснованным нормам, обеспечивающее человеку восстановление его физических и интеллектуальных сил);
3) бедность (потребление благ на уровне сохранения работоспособности как границы
воспроизводства рабочей силы);
4) нищета (минимально допустимый по биологическим критериям набор благ и услуг,
потребление которых лишь позволяет поддерживать жизнеспособность человека).
Обобщающим показателем уровня жизни населения, который бы в достаточной мере отображал наиболее важные черты развития общества является разработанный специалистами Программы развития Организации Объединенных Наций индекс развития человеческого потенциала (ИРЧП).
ИРЧП является составным индексом, включающим три показателя, отражающих наиболее важные аспекты уровня жизни:
1) индекс  ожидаемой продолжительности жизни при рождении; ожидаемой продолжительности жизни при рождении;
2) индекс  достигнутого уровня образования; достигнутого уровня образования;
3) индекс  реального объема ВВП в расчете на душу населения (в долларах США на основе паритета покупательной способности (ППС)). реального объема ВВП в расчете на душу населения (в долларах США на основе паритета покупательной способности (ППС)).
ИРЧП определяется как средняя арифметическая из индексов трех указанных показателей  . .
Индексы  и и  рассчитывается по формуле: рассчитывается по формуле:  , ,
где  , ,  , ,  - фактическое, минимальное и максимальное значение показателя соответственно. - фактическое, минимальное и максимальное значение показателя соответственно.
Для расчетаиндекса  ожидаемой продолжительности жизни при рождениипринимают ожидаемой продолжительности жизни при рождениипринимают  = 25 годам, = 25 годам,  = 85 годам. Таким образом = 85 годам. Таким образом  . .
Для расчетаиндекса  реального объема ВВП в расчете на душу населения принимают реального объема ВВП в расчете на душу населения принимают  = 100 долл., = 100 долл.,  = 40000 долл. = 40000 долл.
Индекс  достигнутого уровня образования определяется по формуле достигнутого уровня образования определяется по формуле  , ,
где  - индекс грамотности среди населения от 15 лет и старше, - индекс грамотности среди населения от 15 лет и старше,  - индекс доли учащихся начальных, средних и высших учебных заведений (для лиц моложе 24 лет). - индекс доли учащихся начальных, средних и высших учебных заведений (для лиц моложе 24 лет).
| . Ряд распределения – это упорядоченное распределение единиц совокупности по определенному варьирующему признаку. Ряды распределения делят на атрибутивные и вариационные. Атрибутивными называются ряды, построенные по качественному признаку. Ряды распределения, построенные по количественному признаку в порядке его возрастания, называются вариационными, а значения количественного признака вариационного ряда – вариантами. Вариационные ряды по способу построения делятся на дискретные и интервальные. Вариационный ряд, в котором варианты задаются одним числом, называется дискретным. Он представляет собой последовательность чисел, которые расположены в порядке возрастания.
Пример 3.1. В результате проведенного статистического наблюдения, имеющего цель – определить распределение рабочих цеха по количеству полных отработанных лет (стажу работы), были получены следующие результаты:
Составим вариационный ряд, в котором варьирующим признаком (X) является стаж работы
Если в дискретном вариационном ряду некоторые варианты повторяются, то для компактности записи ряда их группируют. При этом получается сгруппированный вариационный ряд. Он представляет собой два множества чисел X и F, записанных в виде таблицы, которая состоит из двух строк (столбцов). В верхнюю строку (левый столбец) заносят элементы множества X – варианты  , в нижнюю строку (правый столбец) для каждого варианта записывают соответствующий элемент множества F – частоту варианта , в нижнюю строку (правый столбец) для каждого варианта записывают соответствующий элемент множества F – частоту варианта  – число, показывающее, как часто этот вариант встречается в совокупности. – число, показывающее, как часто этот вариант встречается в совокупности.
Пример. Сгруппированный вариационный ряд, построенный по данным примера 3.1, имеет вид
| Стаж(X)
|
|
|
|
|
|
|
| | Число рабочих
(частота F)
|
|
|
|
|
|
|
|
Таким образом, в сгруппированном вариационном ряду статистическая совокупность оказывается разбитой на k групп причем, 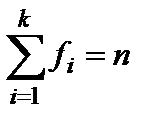 , где n – численность статистической совокупности. , где n – численность статистической совокупности.
Иногда во вторую строку ряда вместо частот помещают относительные частоты вариантов. Относительная частота (частость) 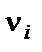 равна частоте варианта равна частоте варианта  , деленной на численность n совокупности – , деленной на численность n совокупности –  . Относительная частота равна доле варианта в совокупности. . Относительная частота равна доле варианта в совокупности.
8.Корреляционный анализ. Определение тесноты связи. Коэффициент линейной
корреляции К. Пирсона. Универсальный коэффициент корреляции R2. Пример вычисления.
Частным случаем статистической связи является корреляционная связь (от английского correlation – соответствие), при котором разным значениям факторного признака соответствуют различные средние значения результативного признака. Корреляционная связь двух признаков (переменных) называется парной корреляцией. Если на результативный признак оказывают влияние несколько факторов, говорят о множественной корреляции. Измерение тесноты связи между варьирующими признаками, выявление и оценка факторов, оказывающих наибольшее влияние на результативный признак, являются предметом корреляционного анализа. Для выявления наличия и характера корреляционной связи в статистике используется ряд методов. При небольшом числе наблюдений наличие корреляционной связи между двумя признаками x и y можно установить методом сопоставления двух рядов. Этот метод заключается в том, что формируется таблица, в одну из строк (столбцов) которой вписываются в порядке возрастания значения факторного признака, а в другую – соответствующие значения результативного признака. В результате сопоставления значений признаков делается вывод о наличии или отсутствии корреляционной связи.
При большом числе наблюдений для выявления корреляционной связи между двумя количественными показателями используют метод группировок. Проводится группировка единиц по факторному признаку x и для каждой выделенной (i -й) группы рассчитывается среднее значение результативного признака  . Если результативный признак y зависит от факторного x, то и в изменении среднего значения результативного признака будет прослеживаться определенная закономерность. . Если результативный признак y зависит от факторного x, то и в изменении среднего значения результативного признака будет прослеживаться определенная закономерность.
Статистические данные могут быть представлены и в другой форме, в виде таблицы, в которой приведено комбинационное распределение единиц совокупности по двум признакам. Такие таблицы называют таблицами взаимной сопряженности.
Если оба признака, по которым дано распределение совокупности, – количественные, такая таблица называется корреляционной. Корреляционная таблица строится по типу «шахматной», в первом и итоговом столбцах таблицы записываются в виде вариационного ряда (дискретного или интервального) распределение значений факторного признака x, а в верхней и итоговой строках –распределение значений результативного признака y. В клетку таблицы, которая находится на пересечении строки, соответствующей значению факторного признака 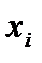 , и столбца, соответствующего значению результативного признака , и столбца, соответствующего значению результативного признака  ,вписывается частота совместного появления этих значений признаков – число ,вписывается частота совместного появления этих значений признаков – число  элементов совокупности, у которых значение факторного признака равно элементов совокупности, у которых значение факторного признака равно 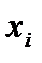 , а результативного признака равно , а результативного признака равно  . .
О наличии и виде корреляционной связи можно судить по расположению частот в корреляционной таблице. Если частоты расположены в клетках таблицы беспорядочно, это говорит об отсутствии связи между группировочными признаками или о том, что их корреляционная связь – слабая. Если же частоты сконцентрированы ближе к одной из диагоналей и к центру таблицы, это свидетельствует о наличии зависимости между  и и  , близкой к линейной. Концентрация частот вокруг диагонали, проведенной из левого верхнего угла таблицы в правый нижний угол, говорит о прямой зависимости, концентрация частот вокруг другой диагонали – об обратной зависимости. , близкой к линейной. Концентрация частот вокруг диагонали, проведенной из левого верхнего угла таблицы в правый нижний угол, говорит о прямой зависимости, концентрация частот вокруг другой диагонали – об обратной зависимости.
Выводы о наличии или отсутствии корреляции между двумя переменными, а также о ее характере можно сделать графическим методом – путем построения и анализа поля корреляции. Поле корреляции (корреляционное поле) – это множество точек на плоскости Oxy, каждая точка которого c координатами x и y соответствует единице совокупности, у которой значение факторного признака равно  , а результативного – равно , а результативного – равно  . Поле корреляции, по существу, представляет собой ту же корреляционную таблицу, в клетках которой вместо частот проставлены точки, число которых равно соответствующей частоте. По характеру расположения точек делается вывод о наличии или отсутствии связи, а если связь – линейная, то является она прямой или обратной. Если корреляционное поле можно оконтурить кривой в виде эллипса, это свидетельствует о наличии линейной зависимости между факторным и результативным признаками. . Поле корреляции, по существу, представляет собой ту же корреляционную таблицу, в клетках которой вместо частот проставлены точки, число которых равно соответствующей частоте. По характеру расположения точек делается вывод о наличии или отсутствии связи, а если связь – линейная, то является она прямой или обратной. Если корреляционное поле можно оконтурить кривой в виде эллипса, это свидетельствует о наличии линейной зависимости между факторным и результативным признаками.
Недостаток приведенных выше методов исследования заключается в том, что они позволяют провести лишь качественный анализ задачи и ответить на вопрос, имеется ли корреляционная связь и каков ее характер, но не позволяют оценить степень тесноты связи факторного и результативного признаков.
Если число значений, которые принимает каждый из двух качественных признаков, оказывается большим, чем два, теснота связи между этими признаками измеряется с помощью коэффициентов взаимной сопряженности К. Пирсона и А.А.Чупрова.
Коэффициент взаимной сопряженности Пирсона вычисляется по формуле
 , ,
где  . .
|
Поиск по сайту:
|
 ожидаемой продолжительности жизни при рождении;
ожидаемой продолжительности жизни при рождении; достигнутого уровня образования;
достигнутого уровня образования; реального объема ВВП в расчете на душу населения (в долларах США на основе паритета покупательной способности (ППС)).
реального объема ВВП в расчете на душу населения (в долларах США на основе паритета покупательной способности (ППС)). .
. и
и  рассчитывается по формуле:
рассчитывается по формуле:  ,
, ,
,  ,
,  - фактическое, минимальное и максимальное значение показателя соответственно.
- фактическое, минимальное и максимальное значение показателя соответственно. ожидаемой продолжительности жизни при рождениипринимают
ожидаемой продолжительности жизни при рождениипринимают  = 25 годам,
= 25 годам,  = 85 годам. Таким образом
= 85 годам. Таким образом  .
. реального объема ВВП в расчете на душу населения принимают
реального объема ВВП в расчете на душу населения принимают  = 100 долл.,
= 100 долл.,  = 40000 долл.
= 40000 долл. достигнутого уровня образования определяется по формуле
достигнутого уровня образования определяется по формуле  ,
, - индекс грамотности среди населения от 15 лет и старше,
- индекс грамотности среди населения от 15 лет и старше,  - индекс доли учащихся начальных, средних и высших учебных заведений (для лиц моложе 24 лет).
- индекс доли учащихся начальных, средних и высших учебных заведений (для лиц моложе 24 лет). , в нижнюю строку (правый столбец) для каждого варианта записывают соответствующий элемент множества F – частоту варианта
, в нижнюю строку (правый столбец) для каждого варианта записывают соответствующий элемент множества F – частоту варианта  – число, показывающее, как часто этот вариант встречается в совокупности.
– число, показывающее, как часто этот вариант встречается в совокупности.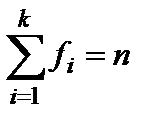 , где n – численность статистической совокупности.
, где n – численность статистической совокупности.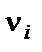 равна частоте варианта
равна частоте варианта  . Относительная частота равна доле варианта в совокупности.
. Относительная частота равна доле варианта в совокупности. . Если результативный признак y зависит от факторного x, то и в изменении среднего значения результативного признака будет прослеживаться определенная закономерность.
. Если результативный признак y зависит от факторного x, то и в изменении среднего значения результативного признака будет прослеживаться определенная закономерность.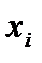 , и столбца, соответствующего значению результативного признака
, и столбца, соответствующего значению результативного признака  ,вписывается частота совместного появления этих значений признаков – число
,вписывается частота совместного появления этих значений признаков – число  элементов совокупности, у которых значение факторного признака равно
элементов совокупности, у которых значение факторного признака равно  и
и  , близкой к линейной. Концентрация частот вокруг диагонали, проведенной из левого верхнего угла таблицы в правый нижний угол, говорит о прямой зависимости, концентрация частот вокруг другой диагонали – об обратной зависимости.
, близкой к линейной. Концентрация частот вокруг диагонали, проведенной из левого верхнего угла таблицы в правый нижний угол, говорит о прямой зависимости, концентрация частот вокруг другой диагонали – об обратной зависимости. . Поле корреляции, по существу, представляет собой ту же корреляционную таблицу, в клетках которой вместо частот проставлены точки, число которых равно соответствующей частоте. По характеру расположения точек делается вывод о наличии или отсутствии связи, а если связь – линейная, то является она прямой или обратной. Если корреляционное поле можно оконтурить кривой в виде эллипса, это свидетельствует о наличии линейной зависимости между факторным и результативным признаками.
. Поле корреляции, по существу, представляет собой ту же корреляционную таблицу, в клетках которой вместо частот проставлены точки, число которых равно соответствующей частоте. По характеру расположения точек делается вывод о наличии или отсутствии связи, а если связь – линейная, то является она прямой или обратной. Если корреляционное поле можно оконтурить кривой в виде эллипса, это свидетельствует о наличии линейной зависимости между факторным и результативным признаками. ,
, .
.