Основная тенденция развития (тренд) представляет собой достаточно устойчивое изменение уровня явления во времени, свободное от случайных колебаний. Модель уровня ряда динамики имеет вид
z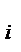 
= 
+ 
,
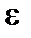где z 
– уровень ряда, 
– средний уровень ряда,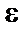 
– случайная составляющая ряда. Ряд динамики называется стационарным, если в нем отсутствует тенденция роста. В стационарном ряду 
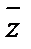= Const и 
= 0. Это значит, что уровни ряда совершают колебания относительно некоторого среднего постоянного значения. Если стационарный ряд динамики разбить на ряд равных частей, то средние уровни по этим частям не должны существенно различаться. При наличии тенденции к изменению среднего уровня ряда динамики, средний уровень следует рассматривать как функцию времени. Методы анализа основной тенденции в рядах динамики разделяются на три группы:
метод укрупнения интервалов;
метод скользящей средней;
метод аналитического сглаживания.
Метод укрупнения интервалов. Если интервалы ряда динамики выбраны таким образом, что средние уровни по ним не позволяют увидеть тенденцию развития явления, переходят к расчету уровней за большие промежутки времени, увеличивая длину каждого интервала.
Метод скользящей средней. Этот метод является разновидностью метода укрупнения интервалов. Он заключается в том, что сначала вычисляется средний уровень из определенного числа, обычно нечетного, первых по счету уровней ряда. Затем – из такого же числа уровней, начиная со второго, затем – с третьего и т.д. Таким образом, средняя как бы скользит по временному ряду от его начала к концу, при этом каждый раз отбрасывается один уровень в начале укрупненного интервала и добавляется один уровень в конце интервала.
|
|
Скользящие средние с продолжительностью периода, равной 3, имеют вид
; 
; 
и т.д.
Полученные значения средних приписываются к середине укрупненного интервала.
Метод аналитического выравнивания. Аналитическое выравнивание ряда динамики основано на выборе математической модели тренда. При этом фактические уровни ряда заменяются уровнями, которые вычислены на основе некоторой функции, выбранной в предположении, что она наилучшим образом описывает эмпирические данные. В результате приходят к трендовой модели уровня ряда динамики, задаваемой формулой (7.3.1).
На практике по имеющемуся ряду динамики задают вид функции 
и определяют ее параметры, а затем анализируют поведение отклонений значений ряда динамики от тенденции.
Выбор вида зависимости осуществляется на основе анализа динамики изучаемого явления. Линейная зависимость выбирается в случаях, когда в исходном динамическом ряду наблюдаются более или менее постоянные абсолютные цепные приросты. Параболическая зависимость используется, когда в исходном ряду динамики абсолютные цепные приросты обнаруживают некоторую тенденцию развития, но абсолютные цепные приросты абсолютных цепных приростов тенденции развития не проявляют. Экспоненциальная зависимость применяется, если в ряду динамики наблюдается более или менее постоянный относительный рост (устойчивость цепных темпов роста, темпов прироста, коэффициентов роста).
Выбор формы кривой может быть основан на анализе графического изображения уровней динамического ряда; при этом целесообразно воспользоваться графическим изображением сглаженных уровней, в которых случайные колебания погашены.
|
|
При выборе параметров функций чаще всего используют метод наименьших квадратов, который обеспечивает минимум суммы квадратов отклонений фактических уровней 
ряда динамики от выровненных значений – значений функции , вычисленных при тех же значениях времени 
min.
Процедура вычислений, проводимых в соответствии с методом наименьших квадратов (МНК), подробно изложена в §6.2.
Система нормальных уравнений, получаемых в результате применения МНК, упрощается, если отсчет времени проводить от середины ряда динамики. При нечетном числе уровней ряда точка, расположенная в середине ряда, принимается за нуль. Отсчетам, предшествующим средней точке, приписываются значения -1, -2, -3 и т.д., последующим – значения 1, 2, 3, и т.д. Если число уровней ряда – четное, двум уровням, находящимся в середине ряда, приписываются значения –1 и +1, а предшествующим и последующим уровням – значения ±3, ±5, ±7 и т.д.
При таком выборе отсчета времени система нормальных уравнений упрощается и при выравнивании по прямой 
принимает вид
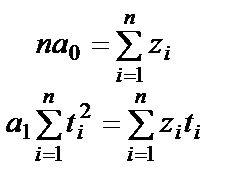
Аналитическое сглаживание позволяет произвести оценку уровня исследуемого явления для периодов, относительно которых нет исходных данных. Нахождение по имеющимся данным за определенный период времени недостающих значений признака внутри этого периода называется интерполяцией. Нахождение значений этого признака за пределами анализируемого периода называется экстраполяцией. Применение экстраполяции при прогнозировании тенденции развития основано на предположении, что основные факторы, определяющие выявленную закономерность, сохранятся и в будущем.
|
|
Агрегатный индекс цены, позволяющий оценить влияние изменения цен на общую стоимость продукции, в форме Ласпейреса имеет вид
= 
.
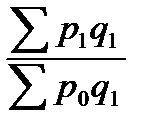Агрегатный индекс физического объема продукции, характеризующий изменение выпуска совокупности продукции разных видов в форме Э. Ласпейреса, имеет вид
= 
.
Здесь: 
и 
– количество выработанных единиц продукции в отчетном и базисном периодах; 
– цена единицы продукции в базисном периоде.
Агрегатный индекс цен в форме Пааше записывается в виде
= .
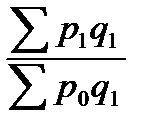Агрегатный индекс цен Фишера определяется формулой
.
Агрегатный индекс товарооборота рассчитывается по формуле
= 
.