Стратегии, которые выбирают игроки в отдельной матричной игре, называются чистыми стратегиями. Поэтому решение матричной игры называется в чистых стратегиях.
В качестве показателя, относительно которого определяется эффективность выбора стратегий игроками определим гарантированный выигрыш игрока А и гарантированный проигрыш игрока В.
Определение. В матричной игре гарантированным выигрышем для стратегии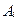 
игрока А называется максимальный выигрыш 
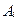, который он может получить, выбрав стратегию , вне зависимости от игры игрока В.
Индекс в значении выигрыша поясняет, что максимальный выигрыш рассматривается для игрока А
Гарантированный выигрыш для данной стратегии 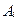игрока А меньше либо равен выигрышу игрока А при заданной его стратегии и любой стратегии игрока В: 
, 
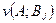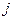= 1, 2, …, 
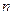. Значит, гарантированный выигрыш для стратегии 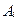равен наименьшему выигрышу игрока А, при выборе игроком В своих стратегий: = 
.
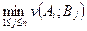Определение. В матричной игре гарантированным проигрышем для стратегии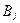 
игрока В называется минимальный проигрыш 
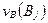, который он может получить вне зависимости от игры игрока А.
Гарантированный проигрыш для стратегии 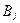больше либо равен проигрышу при этой стратегии и любой стратегии игрока А: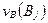 
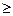
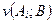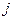, = 1, 2, …, 
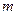. Гарантированный проигрыш равен наибольшему проигрышу игрока В, при выборе игроком А своих стратегий: = 
.
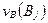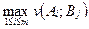Индекс в значении проигрыша 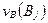, поясняет, что он определяется для игрока В.
Гарантированный выигрыш и гарантированный проигрыш можно рассматривать как показатели неслучайности матричной игры, определяют потенциалы игроков в игре.
В качестве оптимальной стратегии игрок А выбирает стратегию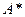 
, при которой гарантированный выигрыш будет наибольшим: 
= 
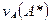. Максимальное значение для всех стратегий игрока А гарантированного выигрыша называется нижней ценой игры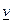 
= .
Игрок В в качестве оптимальной стратегии выбирает стратегию 
, при которой из всех его стратегий гарантированный проигрыш будет наименьшим: 
= 
.
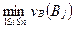Максимальное значение для всех стратегий игрока А гарантированного выигрыша называется ниж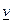ней ценой игры = , а минимальное значение гарантированных проигрышей игрока В для всех его стратегий – верхней ценой игры = .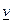
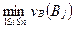Оптимальные стратегии в матричной игре выбираются на основе, так называемых, принципов максимина и минимакса, а сами выбранные стратегии называются максиминной для игрока А и минимаксной для игрока В.
Заметим, что нижняя и верхняя цена игры удовлетворяют условию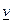 
.
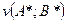
Пример 1. Задана платёжная матрица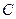 
= 
. Определить оптимальные стратегии игрока А и игрока В, а также нижнюю и верхнюю цены игры.
Решение. Платёжную матрицу представим таблицей, в которой в последнем столбце определим гарантированные выигрыши игрока А как минимальные значения выигрышей в строках, а в последней строке определим гарантированные проигрыши игрока В как максимальные значения проигрышей в столбцах (табл. 1).
Таблица 1