Графическим способом решаются не все матричные игры. Более универсальным методом решения матричных игр является линейно-программный способ. Для его применения матричная игра представляется в виде пары задач линейного программирования для игроков с условиями максимизации гарантированного выигрыша игрока А и минимизации гарантированного проигрыша игрока В.
Составим эти задачи. Пусть 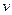 выигрыш игрока А, который он получит при любой стратегии игрока В. Нужно определить максимальное значение этого выигрыша.
выигрыш игрока А, который он получит при любой стратегии игрока В. Нужно определить максимальное значение этого выигрыша.
Выигрыш игрока А 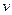 , который он получит вне зависимости игры игрока В, удовлетворяет условию: выигрыш игрока А для любой стратегии игрока В больше либо равен выигрыша
, который он получит вне зависимости игры игрока В, удовлетворяет условию: выигрыш игрока А для любой стратегии игрока В больше либо равен выигрыша 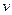 :
: 
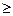
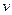 ,
, 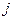 = 1, 2, …, m. Также выполняется условие нормировки для вероятностей стратегий игрока А:
= 1, 2, …, m. Также выполняется условие нормировки для вероятностей стратегий игрока А:  =1. Цель задачи
=1. Цель задачи 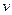
 max. Получим задачу линейного программирования, которую назовём задачей для игрока А:
max. Получим задачу линейного программирования, которую назовём задачей для игрока А:
 (1)
(1)

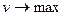
Обозначим через 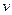 проигрыш игрока В, который он получит при любой стратегии игрока А. Тогда проигрыш игрока В для любой стратегии игрока А больше либо равен проигрыша
проигрыш игрока В, который он получит при любой стратегии игрока А. Тогда проигрыш игрока В для любой стратегии игрока А больше либо равен проигрыша 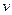 :
: 
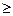
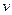 ,
,  = 1, 2, …, n. Для вероятностей стратегий игрока В также выполняется условие нормировки:
= 1, 2, …, n. Для вероятностей стратегий игрока В также выполняется условие нормировки:  =1. Цель задачи
=1. Цель задачи 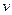
 min. Это тоже задача линейного программирования, которую назовём задачей для игрока В:
min. Это тоже задача линейного программирования, которую назовём задачей для игрока В:
 (2)
(2)


Предположим, что в обеих задачах 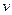
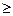 0. Разделим все ограничения в задачах на
0. Разделим все ограничения в задачах на 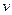 . Получим следующие задачи.
. Получим следующие задачи.
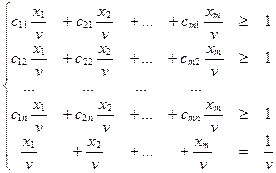 (3),
(3),  (4).
(4).
Определим для обеих задач новые переменные:  =
= 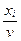 ,
,  =1, 2, …, m;
=1, 2, …, m;  =
=  ,
, 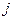 =1, 2, …, n. Так как в задачах для игроков
=1, 2, …, n. Так как в задачах для игроков 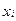
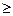 0,
0,  =1, 2, …, m;
=1, 2, …, m; 
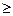 0,
0, 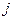 =1, 2, …, n; а по предположению
=1, 2, …, n; а по предположению 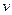
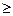 0, то
0, то 
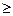 0,
0,  =1, 2, …, m,
=1, 2, …, m, 
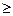 0,
0, 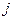 =1, 2, …, n. Целевые функции в задачах определим:
=1, 2, …, n. Целевые функции в задачах определим:  =
=  – для задачи игрока А, и
– для задачи игрока А, и 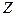 =
=  – для задачи игрока В. Так как в задаче для игрока А,
– для задачи игрока В. Так как в задаче для игрока А, 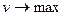 , то
, то
 =
= 
 . В задаче для игрока В
. В задаче для игрока В  , тогда
, тогда 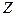 =
= 
 . В результате получим преобразованные задачи для игроков.
. В результате получим преобразованные задачи для игроков.
Для игрока А Для игрока В
 (5)
(5)  (6)
(6)




Преобразованные задачи игроков являются двойственными друг к другу. При этом прямой задачей будет задача для игрока В, а двойственной – задача для игрока А. Решая одну из них, одновременно решаем и другую. Эти задачи можно решить симплекс – методом.
Переход к решению исходных задач для игроков осуществляется следующим образом.
Пусть  =
=  ,
,  и
и  =
=  ,
, 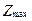 – решения пары преобразованных задач игроков.
– решения пары преобразованных задач игроков.
Переменные исходных и преобразованных задач связаны формулами:  =
= 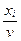 ,
,  =1, 2, …, m;
=1, 2, …, m;  =
=  ,
, 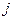 =1, 2, …, n. Целевые функции задач связаны с выигрышем и проигрышем игроков
=1, 2, …, n. Целевые функции задач связаны с выигрышем и проигрышем игроков  ,
,  . Поэтому переход к исходным задачам осуществляется преобразованиями:
. Поэтому переход к исходным задачам осуществляется преобразованиями: 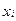 =
=  ,
,  =1, 2, …, m;
=1, 2, …, m;  =
=  ,
, 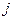 =1, 2, …, n. Целевые функции задач связаны с выигрышем и проигрышем игроков
=1, 2, …, n. Целевые функции задач связаны с выигрышем и проигрышем игроков  ,
,  . Тогда
. Тогда 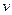 =
=  и
и 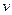 =
=  . Тогда формулы перехода от решения преобразованных задач к решению исходных задач следующие:
. Тогда формулы перехода от решения преобразованных задач к решению исходных задач следующие:  =
=  ,
,  =1, 2, …, m;
=1, 2, …, m;  =
=  ,
, 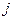 =1, 2, …, n;
=1, 2, …, n;  =
=  или
или  =
=  .
.
Пример 4. Для матричной игры с платёжной матрицей 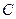 =
=  определить оптимальные стратегии игроков и цену игры линейно – программным способом.
определить оптимальные стратегии игроков и цену игры линейно – программным способом.
Решение. Отметим, что в платёжной матрице все элементы строго больше нуля, поэтому цена игры в задаче будет тоже строго больше нуля. Поэтому можно использовать линейно – программный способ решения. Составим преобразованные задачи для игрока А и для игрока В.
Для игрока А Для игрока В
 (7)
(7)  (8)
(8)


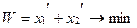

Составим симплекс – таблицу для пары двойственных задач. Полагаем, что прямой задачей будет задача для игрока В. Пометим её номером ноль, полагая таблицу исходной.

| 
| 
| 1, 
| |

| ||||
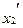
| ||||
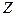 ,1 ,1
| –1 | –1 | –1 |
Проверяем признак допустимости плана. Так как элементы единичного столбца  =1 и
=1 и  =1 больше либо равны нуля, то таблица соответствует допустимому плану.
=1 больше либо равны нуля, то таблица соответствует допустимому плану.
Проверяем таблицу на оптимальность. Так как в Z – строке есть строго отрицательные элементы, например
 = –1, то таблице соответствует неоптимальному плану. 1) Так как
= –1, то таблице соответствует неоптимальному плану. 1) Так как 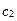 = –1<0, то второй столбец выбираем разрешающим столбцом. Элементы второго столбца выделим серым цветом. 2) Разрешающую строку выбираем по минимальному симплексному отношению.
= –1<0, то второй столбец выбираем разрешающим столбцом. Элементы второго столбца выделим серым цветом. 2) Разрешающую строку выбираем по минимальному симплексному отношению.  =
= 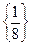 =
=  ;
;  =
=  =1.
=1.  =
=  . Первую строку выбираем разрешающей строкой. Элементы разрешающей строки выделим тоже серым цветом. 3) Разрешающим будет элемент, расположенный на пересечении разрешающей строки и разрешающего столбца. Это элемент
. Первую строку выбираем разрешающей строкой. Элементы разрешающей строки выделим тоже серым цветом. 3) Разрешающим будет элемент, расположенный на пересечении разрешающей строки и разрешающего столбца. Это элемент  =8. Выделим клетку, где находится этот элемент. 4) Проводим преобразование таблицы с помощью исключений Жордана – Гаусса.
=8. Выделим клетку, где находится этот элемент. 4) Проводим преобразование таблицы с помощью исключений Жордана – Гаусса.

| 
| 
| 1, 
| |

| 1/8 | 1/8 | 3/8 | 1/8 |
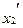
| 47/8 | –1/8 | 37/8 | 7/8 |
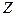 ,1 ,1
| –7/8 | 1/8 | –5/8 | 1/8 |
Переходим к следующей симплекс таблице, которую пометим единицей. В этой таблице меняем переменные  и
и  местами. Остальные переменные оставляем на своих местах. 1) Находим новое значение разрешающего элемента
местами. Остальные переменные оставляем на своих местах. 1) Находим новое значение разрешающего элемента  =
=  ; находим новые значения элементов разрешающей строки. Значения элементов делим на разрешающий элемент.
; находим новые значения элементов разрешающей строки. Значения элементов делим на разрешающий элемент.  =
=  ,
,  =
=  ,
,  =
=  . 3) Вычисляем значения элементов разрешающего столбца. Элементы столбца делим на разрешающий элемент и умножаем на минус единицу.
. 3) Вычисляем значения элементов разрешающего столбца. Элементы столбца делим на разрешающий элемент и умножаем на минус единицу.  =
=  ,
,  =
=  =
=  . 4) Пересчитываем остальные элементы по правилу прямоугольника.
. 4) Пересчитываем остальные элементы по правилу прямоугольника.  =
=  =
=  ,
,  =
=  =
=  ,
, 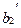 =
=  =
=  ,
,  =
=  =
=  ,
,  =
=  =
=  ,
, 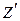 =
=  =
=  .
.
Проверяем таблицу на оптимальность. Она не соответствует оптимальному плану, так как  =
= 
 0. 1) Разрешающий столбец третий, так как
0. 1) Разрешающий столбец третий, так как  =
= 
 0. 2) Симплексные отношения для третьего столбца:
0. 2) Симплексные отношения для третьего столбца:  =
=  = 1;
= 1;  =
=  =
=  .
.  =
= 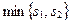 . Разрешающей возьмём вторую строку. 3) Разрешающий элемент
. Разрешающей возьмём вторую строку. 3) Разрешающий элемент  =
=  . 4) Переходим к следующей таблице.
. 4) Переходим к следующей таблице.
Предварительно пересчитаем элементы Z – строки.  =
=  =
=  ,
,  =
=  =
=  =
=  =
=  ,
,  =
=  = =
= = 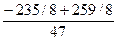 =
=  =
=  . Таблица соответствует оптимальному плану.
. Таблица соответствует оптимальному плану.

| 
| 
| 1, 
| |

| 5/47 | |||

| 7/47 | |||
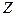 ,1 ,1
| 7/47 | 5/47 | 3/47 | 12/47 |
Таблица соответствует оптимальному плану, так как все элементы. Пересчитаем только элементы Z – строки положительные:  =
=  ,
,  =
=  ,
,  =
=  . рассчитаем элементы единичного столбца.
. рассчитаем элементы единичного столбца.  =
=  =
=  =
=  .
. 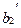 =
=  = =
= =  ,
, 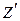 =
=  =
=  =
=  =
=  .
.
Выписываем оптимальное решение пары преобразованных задач.  =
=  ,
,  =
=  ,
,  =
=  ,
, 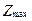 =
=  .
.
Переходим к оптимальному решению пары исходных задач.  =
=  =
=  ;
;  =
=  = =
= = 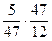 =
=  ,
, 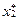 =
=  =
=  =
=  ;
;  =
=  =
=  =
=  ,
, 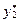 =
=  =
= 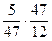 =
=  . Получаем оптимальные стратегии игроков и цену игры:
. Получаем оптимальные стратегии игроков и цену игры:  =
= 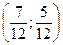 ;
;  =
=  ;
;  =
=  .
.
Ответ:  =
= 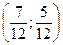 ;
;  =
=  ;
;  =
=  .
.
Если в матричной игре нет гарантии строгой положительности цены, то сначала для неё составляют другую задачу, в которой все элементы платёжной матрицы строго больше нуля. Для этого находят в матрице наибольший по модулю элемент и ко всем элементам матрицы прибавляют число, равное модулю этого числа плюс единица. Тогда в полученной матрице все элементы будут строго больше нуля, а значит и цена игры будет строго больше нуля. Оптимальные стратегии полученной игры будут такие же, как в исходной игре, а цена игры увеличится на добавленное число.
Пример 5. Для матричной игры с платёжной матрицей 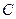 =
= 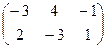 определить оптимальные стратегии игроков и цену игры линейно – программным способом.
определить оптимальные стратегии игроков и цену игры линейно – программным способом.
Решение. В этой матричной игре есть отрицательные элементы. Гарантии строгой положительности цены игры нет. Более того, мы её уже находили графическим способом, и она была меньше нуля. Наибольший модуль имеет отрицательное число равное –3, их даже два. Тогда в качестве числа, которое прибавим к элементам матрицы возьмём  =
=  =3+1=4. Мы получим платёжную матрицу
=3+1=4. Мы получим платёжную матрицу 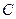 =
=  , которую уже решили линейно – программным способом. Решение матричной игры с изменённой платёжной матрицей будет следующим:
, которую уже решили линейно – программным способом. Решение матричной игры с изменённой платёжной матрицей будет следующим:  =
= 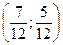 ;
;  =
=  ;
;  =
=  .
.
Переходим к решению исходной матричной игры. Оптимальные стратегии будут такими же:  =
= 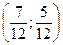 ;
;  =
=  , а цена игры равна:
, а цена игры равна:  =
=  =
=  –4=
–4=  .
.
Мы получили такое же решение, как и в примере 1.
Таким образом, чтобы решить задачу линейно – программным способом, нужно проверить, все её элементы строго больше нуля или нет. Если есть отрицательные элементы, то нужно предварительно прибавить число  , которое равняется наибольшему из модулей отрицательных элементов матричной игры плюс единица.
, которое равняется наибольшему из модулей отрицательных элементов матричной игры плюс единица.