Смешанные стратегии игроков

Рассмотрим случай, когда матричная игра играется большое число раз. Тогда у игроков появляется возможность сочетать свои стратегии. Для каждой стратегии игроков можно задать вероятность, с которой игрок выбирает каждую свою стратегию. Определим – вероятность того, что игрок А выберет стратегию А₁, – вероятность того, что игрок А выберет стратегию А₂, …, – вероятность того, что игрок А выберет стратегию А_m. 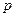Упорядоченный набор = вероятностей стратегий игрока А называется его смешанной стратегией. Аналогично определяется смешанная стратегия = для игрока В, где – вероятность того, что игрок В выберет стратегию В₁, – вероятность того, что игрок В выберет стратегию В₂, …, – вероятность того, что игрок В выберет стратегию В_n.

Матричную игру в таком случае можно рассматривать в смешанных стратегиях. Выигрыш игрока А (проигрыш игрока В) в смешанных стратегиях определятся как = = = , где выигрыш игрока А (проигрыш игрока В) определяемый в чистых стратегиях, элемент платёжной матрицы С = . Цели игроков в матричной игре в смешанных стратегиях остаются такими же как и в чистых стратегиях, а именно, определить максимальный гарантированный выигрыш для игрока А и минимальный гарантированный проигрыш для игрока В.

Для матричной игры в смешанных стратегиях задача ставится так: для заданной платёжной матрицы С нужно определить смешанную стратегию игрока А и смешанную стратегию игрока В, при которых игрок А получит наибольший выигрыш вне зависимости от игры игрока В, а игрок В наименьший проигрыш вне зависимости от игры игрока А.

Определим через выигрыш игрока А, если он выберет стратегию 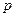, а игрок В выберет свою чистую стратегию 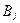. Этот выигрыш будет равняться: = . Аналогично определим : = . Гарантированным выигрышем игрока А для смешанной стратегии 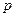будет величина 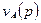= = . Гарантированным проигрышем игрока В для смешанной стратегии – величина = = . Наибольший гарантированный выигрыш игрока А в матричной игре будет = , а наименьший гарантированный проигрыш игрока В в матричной игре = .

Для матричных игр в смешанных стратегиях справедлива основная теорема матричных игр.

Теорема фон Неймана. Каждая конечная игра имеет, по крайней мере, одно оптимальное решение среди смешанных стратегий.

Теорема фон Неймана отвечает на вопрос о существовании решения матричной игры в смешанных стратегиях. Её можно сформулировать так: матричная игра разрешима в смешанных стратегиях.

Если чистая стратегия в оптимальной смешанной стратегии имеет ненулевую вероятность, то её называют активной. Для активных стратегий справедлива теорема.

Теорема об активных стратегиях. Если игрок А придерживается своей оптимальной смешанной стратегии, то его выигрыш остаётся неизменным и равным цене игры , если игрок В не выходит за пределы своих активных стратегий. Также, если игрок В придерживается своей оптимальной стратегии, то его проигрыш будет неизменным, если игрок А не выходит за пределы своих активных стратегий.

Мало того, если один из игроков выйдет за пределы своих активных стратегий, а второй будет придерживаться своей оптимальной стратегии, то первый игрок ухудшит для себя результат игры, игрок А уменьшит проигрыш игрока В, а игрок В увеличит выигрыш игрока А. Отсюда следует важность принципа для игроков: в матричной игре придерживаться своих оптимальных стратегий.