Часть. Двухфакторный дисперсионный анализ без повторений

Занятие 6

ОСНОВЫДИСПЕРСИОННОГО АНАЛИЗА

Цель работы: изучить основные приёмы проведения дисперсионного анализа с помощью функций MS Excel и с использованием инструментов Пакета анализа: «Однофакторный дисперсионный анализ», «Двухфакторный дисперсионный анализ без повторений», «Двухфакторный дисперсионный анализ с повторениями».

Основные положения

Дисперсионный анализ – статистический метод, предназначенный для оценки влияния различных факторов на результаты эксперимента, а также для последующего планирования аналогичных экспериментов.

Пусть на некоторый признак Y воздействует фактор X, который имеет m постоянных уровней. Число наблюдений на каждом уровне n₁, n₂,… n_m.

 

Уровень фактора	Результативный признак	Групповая средняя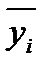
	, ,…,
	, ,…,
…	…	…
	, ,…,

 

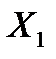
Однофакторный дисперсионный анализ применяется для того, чтобы выяснить, влияет ли фактор Х на случайную величину Y.

Предположим, что случайная величина Y имеет нормальный закон распределения вероятностей с дисперсией σ².

Расчётные формулы:

Групповая средняя :

Общая средняя результативного признака:

,

где - общее число наблюдений;

Общая сумма квадратов отклонений наблюдаемых значений от общей средней:

Факторная сумма квадратов отклонений групповых средних от общей средней (межгрупповая сумма квадратов ), характеризующая рассеяние между группами:

Остаточная сумма квадратов отклонений наблюдаемых значений от своей групповой средней (внутригрупповая сумма квадратов ), характеризующая рассеяние внутри группы:

характеризует воздействие фактора Х, характеризует воздействие случайных причин.

Число степеней свободы рассчитывается по формулам:

, где - общее число наблюдений;

, где m – число уровней фактора;

.

Число степеней свободы связано соотношением:

Оценки дисперсий:

; ;

Рассчитаем наблюдаемое значение критерия Фишера по формуле:

.

Если < , то следует принять гипотезу и отвергнуть гипотезу , в противном случае гипотезу следует отвергнуть.

Рассмотрим пример.

Пример 1. Имеются четыре партии сырья для текстильной промышленности. Из каждой партии отобрано по несколько образцов и проведены испытания на определение величины разрывной нагрузки:

Номер партии	Разрывная нагрузка,

 

Необходимо выяснить, существенно ли влияние различных партий сырья на величину разрывной нагрузки. Принять уровень значимости α = 0,05.

Сформулируем гипотезы.

H ₀: вид сырья не оказывает влияния на величину разрывной нагрузки.

H ₁: различия между партиями сырья по величине разрывной нагрузки не являются случайными, т.е. величина разрывной нагрузки зависит от вида сырья.

Введём исходные данные в ячейки A1:F5.

В Пакете анализа выберем инструмент «Однофакторный дисперсионный анализ» и в окне диалога введём следующие данные: в разделе Входные данные в поле Входной интервал укажем $A$2:$F$5, в поле Группирование выберем по строкам, отметим Метки в первом столбце и зададим значение Альфа: 0,05. В разделе Параметры вывода в поле Выходной интервал укажем любую свободную ячейку, например, А8.

 

Результаты

В таблице ИТОГИ представлены промежуточные результаты расчётов для каждой партии (Группы): номер партии, число образцов (Счет), суммы разрывной нагрузки по каждой партии (Сумма), среднее арифметическое разрывной нагрузки ─ групповая средняя (Среднее), групповая дисперсия (Дисперсия).

В таблице Дисперсионный анализ представлены результаты дисперсионного анализа: компоненты дисперсии (Источник вариации) Между группами (Факторная) и Внутри групп (Остаточная): SS – суммы квадратов, df – число степеней свободы, MS – средний квадрат (факторная и остаточная дисперсии), F – наблюдаемое значение критерия Фишера, P-Значение – вероятность значимости и F критическое – критическое значение критерия Фишера.

Вывод. Так как =3,71 > , то следует отвергнуть гипотезу H ₀ и принять гипотезу H ₁: различие между сырьём в партиях влияет на величину разрывной нагрузки

Рис.1. Окно диалога инструмента «Однофакторный дисперсионный анализ»

.

 

 

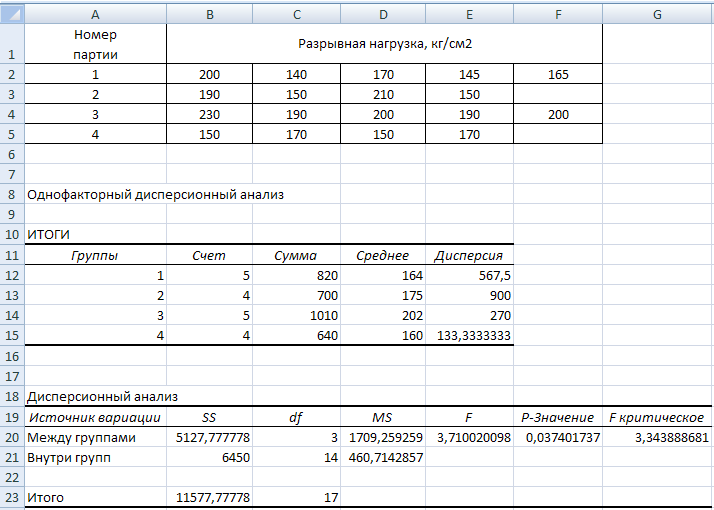
Рис.2. Результаты решения задачи 1 с помощью инструмента «Однофакторный дисперсионный анализ»

Решение задачи 1 с помощью ручного расчёта

Групповые средние:

;

;

Общая средняя результативного признака:

Общая сумма квадратов отклонений наблюдаемых значений от общей средней:

Факторная сумма квадратов отклонений групповых средних от общей средней:

Остаточная сумма квадратов отклонений наблюдаемых значений от своей групповой средней:

11577,78 = 5127,78 + 6450

Число степеней свободы:

; ; .

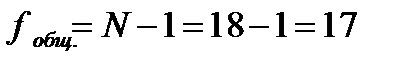Оценки дисперсий:

; .

;

Так как > (3,71 > 3,34), то следует отвергнуть гипотезу и принять гипотезу H ₁: различие между сырьём в партиях влияет на величину разрывной нагрузки.

 

Пример 2. Определить с уровнем α=0,05 значимость различия производительности труда в трёх бригадах рабочих-токарей за десять дней работы (таблица 2, за каждый день приведено среднее число изготовленных за час деталей на одного рабочего и число работавших в этот день рабочих в бригаде).

Таблица 2

Дни	1-я бригада	Число работавших	2-я бригада	Число работавших	3-я бригада	Число работавших

 

Указание: для решения задачи использовать функции MS Excel.

Порядок выполнения задания

Нулевая гипотеза : принадлежность к той или иной бригаде не оказывает влияния на производительность труда.

Конкурирующая гипотеза: H ₁: принадлежность к той или иной бригаде оказывает влияния на производительность труда.

1. Ввести исходные данные в ячейки A1:G11, как показано на рис. 3.

 

Рис.3. Результаты решения задачи 2 с помощью функций MS Excel

 

2. Объединить следующие группы ячеек: A12:B12, A13:B13, A14:B14, A15:D15, A16:D16, A17:D17, и вписать в них тексты, как показано на рис. 3.

3. В ячейки C12, E12, G12 ввести формулы:

=СУММ(C2:C11), =СУММ(E2:E11), =СУММ(G2:G11),

или использовать значок «Автосумма».

4. В ячейку C13 ввести формулу для расчёта групповой средней для 1-ой бригады:

=СУММПРОИЗВ(B2:B11;C2:C11)/C12

5. Выделить ячейку C13 и маркером заполнения протянуть вправо до ячейки G13, а затем удалить в ячейках D13, F13 содержимое с помощью клавиши «Delete». В ячейках E13 и G13 должны получиться формулы:

=СУММПРОИЗВ(D2:D11;E2:E11)/E12

=СУММПРОИЗВ(F2:F11;G2:G11)/G12

6. В ячейки C14, E14 и G14 для вычисления групповых дисперсий ввести формулы:

=СУММПРОИЗВ((B2:B11-C13)^2;C2:C11)/(C12-1),

=СУММПРОИЗВ((D2:D11-E13)^2;E2:E11)/(E12-1),

=СУММПРОИЗВ((F2:F11-G13)^2;G2:G11)/(G12-1).

7. Для вычисления общей средней в ячейку E15 ввести формулу:

=(C13*C12+E13*E12+G13*G12)/(C12+E12+G12)

8. Для вычисления среднего квадрата внутри групп в ячейку E16 ввести формулу:

=(C14*C12+E14*E12+G14*G12)/(C12+E12+G12-3)

9. Для вычисления среднего квадрата между группами в ячейку E17 ввести формулу:

=((C13-E15)^2*C12+(E13-E15)^2*E12+(G13-E15)^2*G12)/(3-1)

10. Для вычисления статистики в ячейку G16 ввести формулу:

= E17/ E16.

11. Для вычисления критического значения в ячейку G17 ввести формулу:

=FРАСПОБР(0,05;2;C12+E12+G12-3).

12. Вывод. Так как =121,89 > , то следует отвергнуть гипотезу и принять гипотезу : различие производительности труда в трёх бригадах значимо с уровнем значимости =0,05.

 

часть. Двухфакторный дисперсионный анализ без повторений

 

Пример 3. При выращивании огурцов на двенадцати участках применялись четыре сорта семян и три технологии выращивания. В таблице 3 приведены показатели урожайности огурцов (в кг/м²). Влияют ли факторы (сорт семян и технология выращивания) на урожайность продукции? Принять =0,05.

Таблица 3

Сорт	Технология 1	Технология 2	Технология 3
Сорт A
Сорт B
Сорт C
Сорт D

 

Указание: для решения задачи использовать инструмент Пакета анализа MS Excel Двухфакторный дисперсионный анализ без повторений.

Порядок выполнения задания

Фактор А – сорт огурцов: четыре уровня. Фактор В – технология: три уровня.

Гипотезы для фактора А

Нулевая гипотеза : сорт огурцов не оказывает влияния на урожайность продукции, т. е. разница в средних значениях по строкам объясняется случайными причинами.

Конкурирующая гипотеза : сорт огурцов оказывает влияние на урожайность продукции, т.е. разница в средних значениях по строкам значима.

Гипотезы для фактора В

Нулевая гипотеза : технология не оказывает влияния на урожайность продукции, т.е. разница в средних значениях по столбцам объясняется случайными причинами.

Конкурирующая гипотеза : технология оказывает влияние на урожайность продукции, т.е. разница в средних значениях по столбцам значима.

1. Ввести данные в ячейки A1:D5, как показано на рис. 5.

2. Загрузить Пакет анализа MS Excel, выполнив действия: Данные → Анализ → Анализ данных.

3. Выбрать инструмент «Двухфакторный дисперсионный анализ без повторений». Нажать кнопку ОК.

4. Ввести в окне диалога в разделе Входные данные: в поле Входной интервал: $A$2:$D$5; Отметить: Метки. Задать Альфа: 0,05.

5. В разделе Параметры вывода в поле Выходной интервал указать А7 (рис. 4).

Рис.4. Окно диалога инструмента «Двухфакторный дисперсионный анализ без повторений»

6. Нажать кнопку ОК. Появятся результаты, представленные на рис. 5.

Результаты

В таблице ИТОГИ представлены промежуточные данные расчётов для каждой строки и для каждого столбца.

В таблице Дисперсионный анализ представлены результаты дисперсионного анализа (см. задание 1). Из таблицы следует: = 1,90; ; = 11,25;

Вывод: так как =1,90 < =4,76, то нулевую гипотезу о том, что сорт огурцов не влияет на урожайность следует принять. Так как, = 11,25 > , то нулевую гипотезу о том, что технология не влияет на урожайность следует отвергнуть и принять конкурирующую гипотезу: технология оказывает значимое влияние на урожайность огурцов.

 

 

Рис.5. Результаты решения задачи 3 с помощью инструмента «Двухфакторный дисперсионный анализ без повторений»