Кулисный механизм (рис. 1), состоящий из маховика 1, кулисы 2 и катка 3, расположен в горизонтальной плоскости и приводится в движение из состояния покоя вращающим моментом 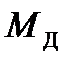 , создаваемым электродвигателем. Заданы массы звеньев механизма; величина вращающего момента; радиус инерции катка и радиусы его ступеней; радиус маховика, представляющего собой сплошной однородный цилиндр, R 1 = 0,36 м; OA = 0,24 м. (табл. 1).
, создаваемым электродвигателем. Заданы массы звеньев механизма; величина вращающего момента; радиус инерции катка и радиусы его ступеней; радиус маховика, представляющего собой сплошной однородный цилиндр, R 1 = 0,36 м; OA = 0,24 м. (табл. 1).
Определить:
· Угловую скорость маховика при его повороте на угол 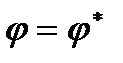 .
.
· Угловое ускорение маховика при его повороте на угол 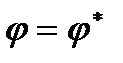 .
.
· Силу, приводящую в движение кулису в положении механизма, когда 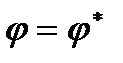 и реакцию подшипника на оси маховика.
и реакцию подшипника на оси маховика.
· Силу, приложенную в центре катка и уравновешивающую механизм в положении, когда  .
.
Записать дифференциальное уравнение движение механизма, используя уравнение Лагранжа второго рода и уравнение движения машины.
Подготовить презентацию к защите курсовой работы, например, в Pоwer Point.

Рис. 1
Таблица 1.
 , кг , кг
|  , кг , кг
| 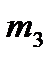 , кг , кг
| 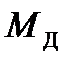 , Н·м , Н·м
|  , м , м
| 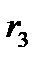 ,м ,м
| 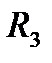 ,м ,м
| 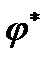 , рад , рад
|
| 0,09 | 0,08 | 0,18 | 5π/4 |
Этап I. Кинематический анализ механизма.
Определение кинематических характеристик
Механизм состоит из трех звеньев. Ведущим является маховик 1, к которому приложен вращающий момент 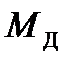 со стороны электродвигателя. От маховика посредством кулисы 2 движение передается ведомому звену 3 – катку. Маховик совершает вращательное движение, кулиса – поступательное, каток – плоское. Начало координат помещаем в точку
со стороны электродвигателя. От маховика посредством кулисы 2 движение передается ведомому звену 3 – катку. Маховик совершает вращательное движение, кулиса – поступательное, каток – плоское. Начало координат помещаем в точку  , ось
, ось 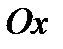 направляем вправо, ось
направляем вправо, ось 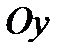 – вверх (рис. 2).
– вверх (рис. 2).
Скорость поступательно движущейся кулисы находим по теореме сложения скоростей, рассматривая движение кулисного камня как сложное. Переносная скорость т. 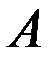 определяет скорость кулисы в ее поступательном движении.
определяет скорость кулисы в ее поступательном движении.
Так как
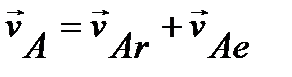 , то
, то 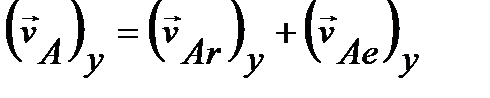 .
.
Откуда 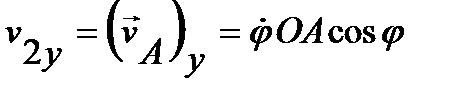 .
.
Скорость центра катка находим из условия пропорциональности скоростей его точек расстояниям до мгновенного центра скоростей
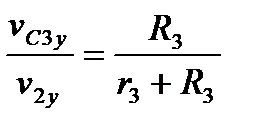 .
.
Откуда
 .
.
Угловую скорость катка находим как отношение скорости его центра к расстоянию до мгновенного цента скоростей

(положительное направление отсчета угла поворота катка – против хода часовой стрелки).
Ускорение поступательно движущейся кулисы, ускорение центра катка, а также угловое ускорение катка находим дифференцированием, соответственно, скорости поступательно движущейся кулисы, скорости центра катка, а также угловой скорости катка. Откуда
 ,
,
 ,
,
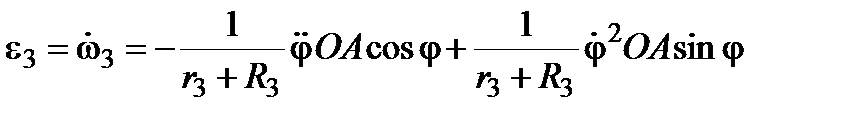 .
.
Укажем векторы 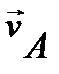 ,
,  ,
,  ,
,  ,
, 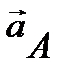 ,
,  ,
,  , и
, и  в положении механизма, изображенном в условии задачи, когда
в положении механизма, изображенном в условии задачи, когда  . Так как динамический расчет еще не проведен и информация об угловой скорости маховика и его угловом ускорении отсутствует, то изображение носит иллюстративный характер. В данном положении и кулиса и каток движутся замедлено. Каток приближается к его крайнему нижнему положению.
. Так как динамический расчет еще не проведен и информация об угловой скорости маховика и его угловом ускорении отсутствует, то изображение носит иллюстративный характер. В данном положении и кулиса и каток движутся замедлено. Каток приближается к его крайнему нижнему положению.

Рис.2
Запись уравнений геометрических связей
Как и раньше, начало координат помещаем в точку  , ось
, ось 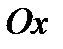 направляем вправо, ось
направляем вправо, ось 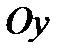 – вверх.
– вверх.
Уравнения связей:
 ,
, 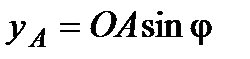 ,
,  ,
, 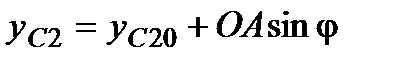 ,
,  .
.
Используя выражения для 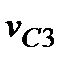 и
и 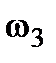 , приходим к равенствам
, приходим к равенствам
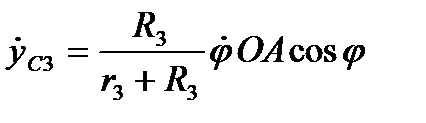 и
и 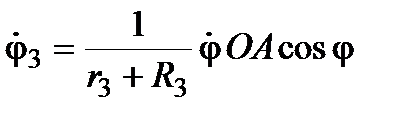 .
.
В результате интегрирования этих дифференциальных уравнений получим
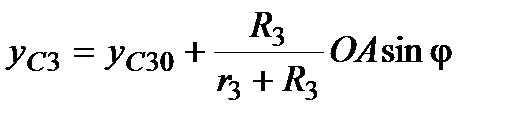 ,
, 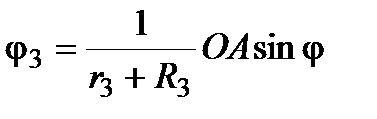 .
.