Найдем силу, которую надо приложить к оси катка, чтобы она уравновешивала действие момента, создаваемого электродвигателем в положении маховика 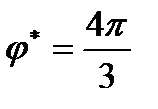 .
.
Для этого воспользуемся принципом виртуальных перемещений
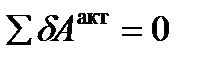
или в аналитической форме, с учетом действующих на систему активных сил:
 .
.
Используя уравнения связей (см. п.1.2)
 ,
, 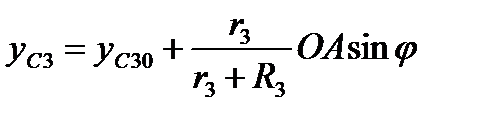 ,
,
находим вариации координат
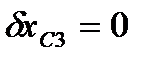 ,
, 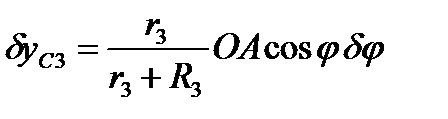 .
.
Подстановка этих соотношений в уравнение принципа виртуальных перемещений дает
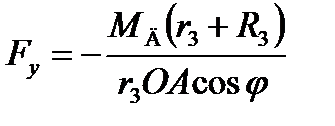 =816,7 Н
=816,7 Н
Любая сила, имеющая такую проекцию на ось  , уравновешивает действие вращательного момента.
, уравновешивает действие вращательного момента.
Этап IV. Дифференциальное уравнение движения кулисного механизма.
Уравнение Лагранжа второго рода
Составим дифференциальное уравнение движения кулисного механизма в форме уравнения Лагранжа второго рода, выбирая за обобщенную координату угол  поворота маховика
поворота маховика
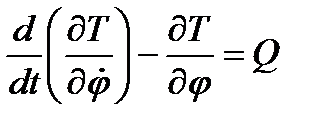 .
.
Обобщенная сила определяется отношением
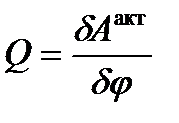 ,
,
где
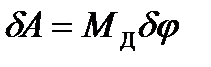 .
.
Тогда
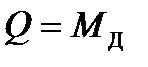 .
.
Воспользовавшись найденным ранее выражением для кинетической энергией системы
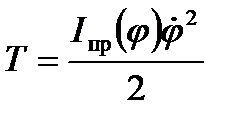 ,
,
находим ее производные

Подстановка найденных значений в уравнение Лагранжа дает
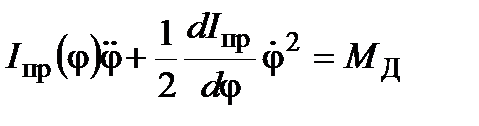 или
или 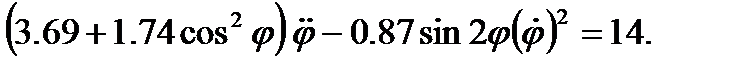 (6)
(6)
Уравнение движения машины
Машиной называется совокупность твердых тел (звеньев), соединенных между собой так, что положение и движение любого звена полностью определяется положением и движением одного звена, называемого ведущим. Если ведущим звеном является кривошип, то уравнение машины записывается в форме
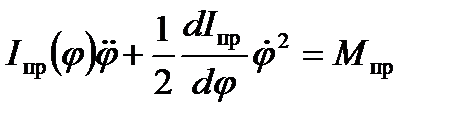 ,
,
 - момент инерции машины, приведенный к оси вращения ведущего звена;
- момент инерции машины, приведенный к оси вращения ведущего звена; 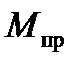 - вращающийся момент, приведенный к оси вращения ведущего кривошипа.
- вращающийся момент, приведенный к оси вращения ведущего кривошипа.
Приведенный момент инерции найден в п.2.1 курсовой работы. Приведенный вращающий момент определяется равенством
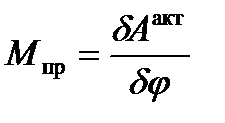 .
.
Для рассматриваемого кулисного механизма
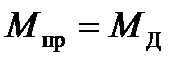 .
.
Запишем дифференциальное уравнение движения машины
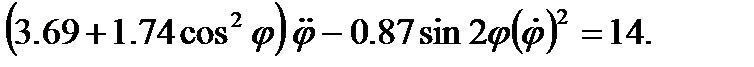 (7)
(7)
Дифференциальные уравнения движения механизма, полученные с помощью теоремы об изменении кинетической энергии (5), уравнения Лагранжа (6) и уравнения движения машины (7) совпадают.
Этап V. Подготовка презентации курсовой работы к защите.
Сведение результатов вычислений в таблицу
В таблице 2 приведены угловая скорость и угловое ускорений маховика, а также динамические и статические усилия.
Таблица 2.
 , рад/с , рад/с
| 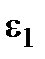 , рад/с2 , рад/с2
| 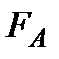 , Н , Н
| 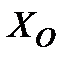 , Н , Н
| 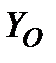 , Н , Н
| 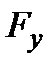 , Н , Н
|
| 5,55 | 7,6 | 117,3 | 117,3 | 816,7 |
ПРИЛОЖЕНИЕ 1
Министерство образования и науки Российской Федерации
ФГАОУ ВПО «Уральский федеральный университет
имени первого Президента России Б.Н.Ельцина»
кафедра теоретической механики
КУРСОВАЯ РАБОТА
по теоретической механике
«ДИНАМИКА КУЛИСНОГО МЕХАНИЗМА»
Вариант 22000011
Студент Иванов И.И.
Группа М-220000
Преподаватель Петров В.С.
Комиссия:
Дата _______________
Оценка ______________
__________________(Ф.И.О.)
__________________(Ф.И.О.)
Екатеринбург
ПРИЛОЖЕНИЕ 2
Министерство образования и науки Российской Федерации
Федеральное государственное автономное образовательное учреждение высшего профессионального образования
«Уральский федеральный университет имени первого Президента России Б.Н.Ельцина »
Кафедра теоретической механики
« УТВЕРЖДАЮ »
Зав. кафедрой __________________
«______» _______________ 2013 г.
Задание № ___ 22000011 ___
На курсовую работу
Студент группы ___ М-220000 _____специальность/направление__________________________________
Фамилия___ Иванов Имя ___ Иван __ Отчество ___ Иванович __
Руководитель работы___ Петров В.С. _____
Срок выполнения с _______ дата выдачи задания ________ по ________15.12.2013 г.______
1.Тема курсовой работы: «ДИНАМИКА КУЛИСНОГО МЕХАНИЗМА»
2.Содержание работы (какие графические задания и расчёты должны быть выполнены): выполнение этапов работы в соответствии с методическими указаниями.
3.Особые дополнительные сведения: еженедельные консультации согласно расписанию.
4. План выполнения курсовой работы
| Наименование элементов работы | Сроки | Примечания | Отметка о выполнении |
| I этап | |||
| II этап | |||
| III этап | |||
| IV этап | |||
| V этап | |||
| Защита |
5.Курсовая работа закончена _______________________________________________________
6.Предварительная оценка работы______________________________________________________________
Руководитель _______________________