Измерение моментов на валу двигателя и на валу нагрузки как уже отмечалось в п.1 производится в данной лабораторной установке с помощью измерительных пружин. Измеряемой величиной является прогиб пружины, значения которого фиксируются индикаторами часового типа в мм: значения прогиба получается умножением числа делений индикатора, отмеченных стрелкой, на цену деления шкалы индикатора. Однако для целей работы необходимы значения действующих моментов на валу двигателя или на его статоре. Поэтому возникает необходимость поставить в соответствие каждому делению шкалы значение соответствующего момента на статоре, рычаг которого изгибает пружину (рис. 4). Графическое изображение такого соответствия называют градуировочной харатеристикой измерительного устройства. Градуировочная характеристика индикаторов линейна (это зависимость угла поворота стрелки индикатора от перемещения его штока). Поэтому вид градуировочной характеристики всего измерительного устройства будет зависеть от вида упругой характеристики измерительной пружины (зависимости ее прогиба от силы, вызывающей этот прогиб). Но основным свойством измерительных пружин является линейность их упругих характеристик. Поэтому получается, что связь между моментом, изгибающим измерительную пружину и числом делений индикатора, т.е. градуировочная харктеристика всего измерительного устройства, будет линейной (рис.9). В таком случае каждому делению шкалы будет соответствовать одинаковое изменение момента, т.е. цена деления или градуировочный коэффициент будут постоянны и равны коэффициенту наклона градуировочной характеристки.
Для экспериментального определения градуировочной характеристики необходимо поворачивать статор выключенного дигателя (или порошкового нагрузочного устройства) вокруг оси двигателя в ту же сторону, в которую он поворачивается при включении питания, моментом, величина которого известна заранее, и отмечать показания индикатора. Известные значения моментов можно получать так: со статором соединяется вспомогателный рычаг, на который вешаются гири определенного веса. Несколько пар значений «момент – показание индикатора» позволяют построить в координатах «число делений – момент» ряд точек; линия проведенная через эти точки и должна быть градуировочной характеритсикой.
Однако при проведении экспериментов появляются погрешности – систематические и случайные, из-за которых точки, соответствующие измерениям оказываются разбросанными в зоне предполагаемой градуировочной характеристики.
Систематической называется погрешность, которая при повторении измерений в неизменных условиях постоянна или изменяется по известному закону. Систематические погрешности вызваны либо постоянно действующими факторами, либо факторами, закон изменения которых известен. Примерами систематических погрешностей являются температурная, методическая погрешности и т. п. Если систематическая погрешность известна, то её можно заранее учесть или исключить из результатов измерения.
Случайной называется погрешность, которая при повторении измерений в практически неизменных условиях изменяется от измерения к измерению. Практика показывает, что отрицательные ошибки встречаются так же часто, как и положительные. Как правило, чем больше ошибка, тем реже она встречается. Случайные погрешности обусловлены влиянием целого ряда изменяющихся факторов. Случайные погрешности нельзя исключить, но путём многократных измерений их влияние на результат измерения можно уменьшить. Достигается это различными методами статистической обработки результатов измерений, среди которых наиболее распространенным является метод наименьших квадратов. Рассмотрим его применение в нашем случае.
Допустим, что мы получили по приведенной выше схеме n пар “момент – число делений индикатора” (обозначим далее в этом разделе моменты буквой y, числа делений – x). Мы знаем, каждой i – ой паре в координатной плоскости XY соответствует точка, которая должна
располагаться на градуировочной прямой
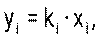
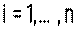 (10)
(10)
где: 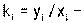 коэффициент наклона i – ой характеристики, которая из-за случайных погрешностей несколко не совпадает с истинной характеристикой, у которой коэффициент наклона (пока нам неизвестный) равен k, и для которой значение измерения было бы:
коэффициент наклона i – ой характеристики, которая из-за случайных погрешностей несколко не совпадает с истинной характеристикой, у которой коэффициент наклона (пока нам неизвестный) равен k, и для которой значение измерения было бы:
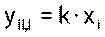 ,
, 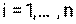 (11)
(11)
Согласно методу наименьших квадратов “истинным” будет то значение коэффициента k, при котором сумма квадратов погрешностей
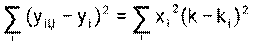 (12)
(12)
будет минимальной. Приравнивая нулю производную по k от правой части
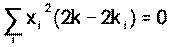 (13)
(13)
и подставляя вместо 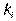 его значение, находим
его значение, находим
 (14)
(14)
Градуировочные характеристики измерительного устройства:
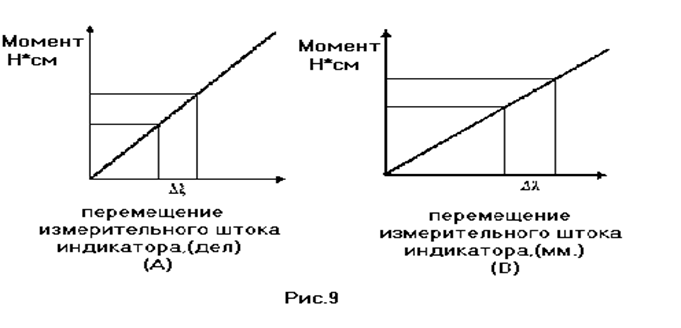 Таблица для рассчета градуировочных коэффициентов k измерителных пружин 11 и 16
Таблица для рассчета градуировочных коэффициентов k измерителных пружин 11 и 16

| 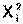
| 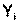
| 
| 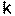
|
| 1 2 3 4 | ||||
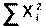
| 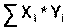
| |||