ПОСЛЕДОВАТЕЛЬНОСТЬ ПРОВЕДЕНИЯ ОПЫТА И РАСЧЁТОВ

 

Дальнейшая работа выполняется в соответствии с заданным вариантом. Объём работы по каждому варианту приведён в табл. 1.

1) Проградуируйте измерительные пружины 11 и 16 (см. п.5).

2) При включённых двигателе 2 и тормозе 4 установите на ноль стрелки индикаторов 12 и

17 поворотом их шкал, легко постукивая при этом по основанию 1 (рис.14).

3) Тумблером 7 включите двигатель 2. Двигатель начнёт вращаться, и загорится сигнальная лампа 9 (рис.14)

4)Тумблером 14 включите порошковый тормоз 4. После этого проведите испытания в

соответствии с указанными в варианте задания режимами работы установки (см. табл. 1)

Частота вращения двигателя n₁ устанавливается поворотом ручки 8 потенциометра и контролируется по тахометру 6. Нагрузочный момент, соответствующий заданным значениям ξ ₂ (в делениях), устанавливается поворотом ручки 15 потенциометра и контролируется по индикатору 17. При изменении момента нагрузки меняется и частота вращения двигателя n₁.Поэтому при проведении испытаний необходимо непрерывно следить за показаниями тахометра 6, регулируя скорость двигателя поворотом ручки 8.

Если увеличение момента нагрузки вызвало остановку двигателя, то надо последний немедленно выключить тумблером 7 или с помощью тумблера 14 и ручки 15 выключить либо уменьшить нагрузку. Остановка включённого двигателя может привести к его перегоранию.

Для каждого из указанных в варианте режимов работы определите и запишите в табл. 3

числа делений ξ _{2 J} индикатора 17, ξ _{1 J} индикатора 1

Варианты заданий (табл.1)

№ вар.	n1	ξ 2	ξ 2	ξ 2	ξ 2	ξ 2

 

 

Экспериментальное определение зависимости момента на двигателе

от момента нагрузки цилиндрического многоступенчатого редуктора

Тарировочные коэффициенты ;

 

Таблица 2.

î2J   дел.	MHJ = î21 * K2   Н*см	î1J   дел.	МДВJ = î1J * K1   Н*см

 

После окончания испытаний выключите установку тумблерами 7 и 14. Расчёт моментов ведётся по формулам:

(32)

Результаты расчётов запишите в табл. 2. Постройте экспериментальную зависимость Мдв=f(Мн)

 

 

Определение теоретических значений коэффициента полезного действия многоступенчатого редуктора

 

z ₂

z ₁ = 31; м = 1 мм; d₁ = м _* z₁ = … мм; i_1-2 = i _3-4 = i _5-6 = i _7-8 = i _9-10 = i _11-12 = —— = …;

z ₁

1 1

z ₂ = 53; м = 1 мм; d₂ = м _* z₂ = … мм; —— + —— = ….;

z ₁ z ₂

η _оп = 0,9; f = 0,1; р – число пар подшипников n₁ = …

Таблица 3.

М Н   Н*см	N Ва ла	М i,   Н*см
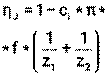
		M4 =	F4 =	C4 =
		M3 =	F3 =	C3 =
		M2 =	F2 =	C2 =
		M1 =	F1 =	C1 =

 

1. Рассчитайте теоретические значения момента на двигателе исследуемого редуктора для тех же условий, для которых проводился эксперимент (см. п Результаты расчёта запишите в табл. 3. Постройте теоретическую зависимость Mдв=f(Мн)

2. Проанализируйте полученные результаты, сравнивая полученную зависимость с зависимостью, полученной опытным путем.

3. Оформите отчёт.

4. Приведите в порядок рабочее место.

 

 

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Чем отличается редуктор от мультипликатора?

2. Типы редукторов, их сравнительные характеристики.

3. Как зависит КПД приборного редуктора от нагрузки?

4. Как влияет увеличение числа колёс зубчатой передачи на её КПД?

5. Чем отличается ступенчатая зубчатая передача от рядового механизма?

6. Как определяется передаточное отношение ступенчатой передачи и рядового механизма?

7. Последовательность проведения эксперимента.

8. Каким образом повышается точность проведения эксперимента?

9. Как производится тарировка?

10. Как влияет жёсткость плоских измерительных пружин 11 и 16 на тарировочные коэффициенты?

11. Объяснить результаты, полученные в работе.

 

(BБ) ОСОБЕННОСТИ РАСЧЁТА ПРИВОДА, СОДЕРЖАЩЕГО ЧЕРВЯЧНЫЙ РЕДУКТОР

(Лабораторная работа № 5)

Червячный редуктор включает следующие элементы (рис.15):

1. Червячную передачу;

2. Опоры качения (две пары).

Червячная передача состоит из двух элементов: специального зубчатого колеса (червяка), изготовленного совместно с валом (выходной вал) и червячного колеса, закреплённого на валу.

Червячная передача обеспечивает передачу

вращения между скрещивающимися под углом 90^º валами. Ведущим элементом является червяк, ведомым – червячное колесо. Достоинством червячной передачи является её компактность, бесшумность работы. Недостатком – наличие большого скольжения червяка относительно червячного колеса (рис.15). Скольжение приводит к большим потерям на трение, в результате чего КПД передачи относительно небольшой. По причине больших потерь на трение червячные колёса или их зубчатые венцы выполняют из дорогостоящих антифрикционных материалов (например, из бронзы).

 

Передаточное отношение червячного редуктора равно:

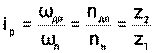(33)

z ₁ — число заходов червяка (В лабораторной установке z ₁ = 2);

z ₂ — число зубьев червячного колеса (В лабораторной установке z ₂=50).

В приводе, содержащем червячный редуктор, зависимость между моментом на двигателе Мдв, действующим на червяк, и моментом нагрузки в соответствии с формулой (6) будет иметь вид:

(34)

где — КПД червячного редуктора. В соответствии с формулой (6) можно определить как:

(35)

2 — количество пар опор.

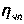— КПД червячной передачи аналитически рассчитывается по формуле (2):

Параметр С для червячной передачи рассчитывается по формуле:

 

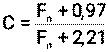(36)

— нормальная сила, действующая на червячное колесо, Н;

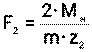— окружное усилие на червячном колесе, Н; (37)

m – модуль червячного колеса, мм (стандартный параметр);

а параметр Ø для червячной передачи рассчитывается по формуле:

(38)

ã = arctg (z1 / q) -- угол подъёма винтовой линии червяка;

ρ = arctg (f / Cos (α)) -- угол трения;

f – коэффициент трения скольжения для материалов сталь-бронза, f = 0,05…0,25

(для лабораторного редуктора выбирается наиболее неблагоприятное значение f = 0,25)

α = 20° -- угол профиля в осевом сечении;

q – коэффициент диаметра червяка, стандартный параметр (в лабораторной передаче q = 40 / 3).

 

КОНСТРУКЦИЯ УСТАНОВКИ

Экспериментальное исследование червячного редуктора проводится на лабораторной установке, кинематическая схема которой дана на рис.17, а конструкция на рис.16. Измерительные устройства установки показаны на рис.12 и рис. 13

Лабораторная установка (рис. 16) имеет основание 1, на котором установлены электрический двигатель 2, червячный редуктор 3, порошковый тормоз 4, создающий момент нагрузки, и пульт управления 5. К ротору электрического двигателя подключен тахометр 6, позволяющий определить частоту вращения в об/мин. Электрический двигатель 2 включается и выключается тумблером 7, а частоту его вращения можно регулировать поворотом ручки потенциометра 8. При включении загорается лампа 9.

Работа редуктора просматривается через прозрачную крышку. Установка подключается к сети постоянного тока напряжением 110 В, мощность электрического двигателя 20 Вт.

 

ТРЕБОВАНИЯ ПО ТЕХНИКЕ БЕЗОПАСНОСТИ

 

Нельзя оставлять установку в заторможенном состоянии с включённым электрическим двигателем, так как в этом случае двигатель может перегореть. При работе на установке прозрачная крышка редуктора должна быть закрыта. Когда ручки 8 и 15 потенциометров (рис. 16) дошли до упоров, не следует их поворачивать чрезмерным усилием руки, что может вывести потенциометры из строя.

При обнаружении неисправностей установки следует немедленно обратиться к учебному мастеру.

ПРАКТИЧЕСКАЯ ЧАСТЬ РАБОТЫ

ГРАДУИРОВКА ИЗМЕРИТЕЛЬНЫХ ПРУЖИН ЭКСПЕРИМЕНТАЛЬНЫМ СПОСОБОМ

Градуировка проводится при выключенных двигателе и тормозе. Перед началом градуировки отодвиньте лабораторную установку от стены и проверьте, упираются ли штоки индикаторов 12 и 17 в измерительные пружины 11 и 16 (рис.12 и 13). Механизмы индикаторов не должны стоять у своих крайних положений.

1) Проградуируйте измерительную пружину 11 индикатора 12. Для этого вставьте до упора малый градуировочный рычаг 20 в отверстие (см. рис.13), находящееся сзади рамы двигателя. Широкая грань рычага должна быть расположена вертикально. Установите на рычаге 20 градуировочный груз 21 весом F_М = 1Н таким образом, чтобы одна из его граней находилась против нулевой отметки. Легко постукивая по основанию ладонью, поворотом шкалы индикатора 12 поставьте большую стрелку на ноль. Упор рамы статора двигателя 2 прижимается к градуировочной пружине 11 под действием усилия, создаваемого винтовой пружиной 22 (рис.13). Градуировочная пружина 11 под действием этого усилия прогибается. При установке индикатора 12 на ноль исключается влияние этой начальной деформации, как и влияние неуравновешенности системы на

показания индикатора

.

Перемещайте градуировочный груз 21 вдоль шкалы рычага 20, устанавливая грань груза против рисок, соответствующих изменению длины плеча ∆L _J на 8, 10, 12, 14, 16, 18, 20 см. При этом внешний момент, действующий на статор двигателя, постепенно возрастает, вызывая увеличение прогиба пружины 11 и перемещение стрелки индикатора. Значения ∆L _J и число делений индикатора ξ _J записывайте в градуировочную табл. 1, При градуировке следите, чтобы рычаг 20 не отошёл от упора.

Изменение внешнего момента на ∆М _{M J}, создаваемое перемещением градуировочного груза на ∆L _J , уравновешивается изменением момента силы измерительной пружины 11, который пропорционален отклонению стрелки индикатора 12:

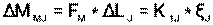(39)

где К _{1 J} -- значение градуировочного коэффициента индикатора 12.

Рассчитайте значения коэффициента К _{1 J} для каждого замера и запишите их в таблицу. Полученные при этом значения не должны заметно отличаться. Вычислите

среднеарифметическое значение коэффициента К ₁ , которое и используйте при дальнейшей работе. При градуировке, как и при работе на установке, следите, чтобы ограничительные вилки не соприкасались с ограничителями, расположенными ниже статора двигателя и тормоза.

2) Проградуируйте измерительную пружину 16 индикатора 17. Последовательность градуировки в этом случае аналогична. В отверстие консоли вала статора тормоза 4 вставьте до упора конец большого градуировочного рычага 24, широкая грань рычага располагается вертикально. Рычаг 24 и индикатор 17 находятся с разных сторон от порошкового тормоза. Установите на рычаге градуировочный груз 25 весом F_М = 5Н так, чтобы боковая грань находилась против отметки 0. Установите на ноль поворотом шкалы стрелку индикатора 17. При этом автоматически устраняется влияние на показания индикатора действия винтовой пружины 26, прижимающей упор 27 к измерительной пружине 16, как и действия неуравновешенности статора тормоза вместе с рычагом 24 и градуировочным грузом 25, когда последний находится у нулевой отметки.

Перемещайте градуировочный груз 25 вдоль градуировочного рычага, последовательно устанавливая одну и ту же его грань у делений, соответствующих значениям ∆L _J , равным 10, 12, 14, 16, 18, 20 см. При этом крутящий момент, действующий на статор тормоза, будет постепенно возрастать, вызывая увеличение прогиба пружины 16 и перемещение стрелки индикатора 17. При градуировке легко постукивайте ладонью по основанию 1. Запишите в табл.1 для каждого из положений груза 25 число делений индикатора ξ _J.

При расчёте градуировочного коэффициента используйте зависимость

, (40)

где К _{2 J} -- значение градуировочного коэффициента для индикатора 17.

Рассчитайте сначала значения К _{2 J} для каждого положения груза 25. Эти значения должны быть близки. Потом определите среднеарифметическое значение градуировочного коэффициента К ₂ , которое и используйте при дальнейшей работе. После градуировки снимите груз 25 и рычаг 26. Обработайте данные таблицы 1,применяя метод наименьших квадратов.

Постройте график зависимости изменения момента тарировочного груза от числа делений индикатора. Градуировочный коэффициент K будет равен тангенсу угла наклона аппроксимирующей прямой.

 

 

ПОСЛЕДОВАТЕЛЬНОСТЬ ПРОВЕДЕНИЯ ОПЫТА И РАСЧЁТОВ

 

Дальнейшая работа выполняется в соответствии с заданным вариантом. Объём работы по каждому варианту приведён в табл. 2.

1) При включённых двигателе 2 и тормозе 4 установите на ноль стрелки индикаторов 12 и

17 поворотом их шкал, легко постукивая при этом по основанию 1 (рис.16).

2) Тумблером 7 включите двигатель 2. Двигатель начнёт вращаться, и загорится сигнальная лампа 9 (рис.16)

3) Тумблером 14 включите порошковый тормоз 4. После этого проведите испытания в

соответствии с указанными в варианте задания режимами работы установки (см. табл. 2)

Частота вращения двигателя n₁ устанавливается поворотом ручки 8 потенциометра и контролируется по тахометру 6. Нагрузочный момент, соответствующий заданным значениям ξ ₂ (в делениях), устанавливается поворотом ручки 15 потенциометра и контролируется по индикатору 17. При изменении момента нагрузки меняется и частота вращения двигателя n₁.Поэтому при проведении испытаний необходимо непрерывно следить за показаниями тахометра 6, регулируя скорость двигателя поворотом ручки 8.

Если увеличение момента нагрузки вызвало остановку двигателя, то надо последний немедленно выключить тумблером 7 или с помощью тумблера 14 и ручки 15 выключить либо уменьшить нагрузку. Остановка включённого двигателя может привести к его перегоранию.

Для каждого из указанных в варианте режимов работы определите и запишите в табл. 3

числа делений ξ _{2 J} индикатора 17, ξ _{1 J} индикатора 1

 

Тарировочная таблица (табл.1)

Измене- Изменение момента Число делений Тарировочный ние плеча тарировочного груза индикатора коэффициент ∆L J, см ∆М J = FМ * ∆L J, ξ J ∆М M J Н*см К J = —— ξ J Н*см /дел

Для индикатора 12: FМ = 1Н 20

Среднее значение тарировочного коэффициента К 1 =   Для индикатора 17: FМ = 5Н

Среднее значение тарировочного коэффициента К 2

 

 

Варианты заданий (табл.2)

№ вар.	n1	ξ 2	ξ 2	Ξ2	ξ 2	ξ 2

 

1) Тумблером 7 включите двигатель 2. Двигатель начнёт вращаться.(рис.14)

2) Тумблером 14 включите порошковый тормоз 4. После этого проведите испытания в соответствии с указанными в варианте задания режимами работы установки (см. табл. 2)

Частота вращения двигателя n₁ устанавливается поворотом ручки 8 потенциометра и контролируется по тахометру 6. Нагрузочный момент, соответствующий заданным значениям ξ ₂ (в делениях), устанавливается поворотом ручки 15 потенциометра и контролируется по индикатору 17. При изменении момента нагрузки меняется и частота вращения двигателя n₁.

Поэтому при проведении испытаний необходимо непрерывно следить за показаниями тахометра 6, регулируя скорость двигателя поворотом ручки 8.

Если увеличение момента нагрузки вызвало остановку двигателя, то надо последний немедленно выключить тумблером 7 или с помощью тумблера 14 и ручки 15 выключить либо уменьшить нагрузку. Остановка включённого двигателя может привести к его перегоранию.

Для каждого из указанных в варианте режимов работы определите и запишите в табл. 3

числа делений ξ _{2 J} индикатора 17, ξ _{1 J} индикатора 12.

 

 

Экспериментальное определение зависимости момента на двигателе

от момента нагрузки червячного редуктора

Тарировочные коэффициенты ;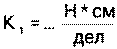

 

 

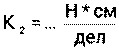
Таблица 3

ξ 2J дел	М Н J = ξ 2J * К 2 Н*см	ξ 1J дел	М ДВ J = ξ 1J * К 1 Н*см

 

После окончания испытаний выключите установку тумблерами 7 и 14. Расчёт моментов ведётся по формулам:

(41)

 

Результаты расчётов запишите в табл. 3. Постройте экспериментальную зависимость Мдв=f(Мн)

 

 

Определение теоретической зависимости зависимости момента на двигателе

от момента нагрузки червячного редуктора

 

 

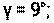
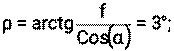
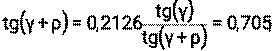
Таблица 4

МН =М2	2МН F2= --------- d2	F 2 Q= ------------ Cos(γ)*Cos(α)	Q + 0, 97 C= ---------- Q + 2,21	tg(γ) η1-2= 1- C----------- tg(γ+ρ)	ηред i = =η1-2 * η2оп	Мн Mдв=----- ηУ * iP

 

1. Рассчитайте теоретические значения момента на двигателе исследуемого редуктора для тех же условий, для которых проводился эксперимент. При расчёте используйте формулу (13). Результаты расчёта запишите в табл. 4. Постройте теоретическую зависимость Mдв=f(Мн)

2. Проанализируйте полученные результаты, сравнивая полученную зависимость с зависимостью, полученной опытным путем.

3. Оформите отчёт.

4. Приведите в порядок рабочее место.

 

(В) ОСОБЕННОСТИ РАССЧЕТА ПРИВОДА, СОДЕРЖАЩЕГО ПЛАНЕТАРНЫЙ РЕДУКТОР

(Лабораторная работа № 6)

Планетарный редуктор представляет собой зубчато–рычажное устройство, в котором геометрические оси одного или нескольких колёс перемещаются в пространстве. Планетарные передачи обладают рядом достоинств. Переход от обычных передач к планетарным обеспечивает снижение веса в 1,5 – 5 раз, приводит к уменьшению габаритов (при тех же передаточных отношениях). В зависимости от схемы планетарные передачи могут осуществлять передаточные отношения от 3 до 1000 при КПД от 0,98 до 0,01 соответственно.

Ведущий и выходной валы расположены соосно.

Планетарный механизм состоит из трёх частей:

1) солнечного колеса, геометрическая ось которого не изменяет своего положения в пространстве;

2) сателлита, геометрическая ось которого перемещается по окружности;

3) водила, поддерживающего ось сателлита при его вращении.

При работе планетарной передачи сателлит обегает вокруг солнечного колеса подобно тому, как планеты движутся вокруг солнца. Поэтому передача и называется планетарной.

Планетарные передачи могут быть использованы для сложения различных движений.

В этом случае они называются дифференциалами.

Меньшие размеры и вес планетарных передач по сравнению с соответствующими зубчатыми передачами с неподвижными осями объясняются тем, что применение двух или трёх сателлитов позволяет уменьшить нагрузку на зубья колёс и использовать колёса с меньшими модулями и диаметрами. Передачи отличаются также высокой надёжностью и малыми потерями на трение.

 

 

На рис.18 показана кинематическая схема планетарного редуктора, который использован в лабораторной установке. Он состоит из двух спаренных планетарных передач. Солнечные колёса имеют числа зубьев z₁ = 17 и z₄ = 87, причём колесо z₄ неподвижно.

Числа зубьев сателлитов z₂ = 87 и z₃ = 17.

Модуль зацепления m = 0,8 мм. Сателлиты жёстко закреплены на общей оси 2. Их угловые скорости одинаковы ω₂ = ω₃. Водило (выходной вал) 3 поддерживает перемещающуюся по окружности ось сателлитов. Ведущим является солнечное колесо z₁, ведомым кинематическим звеном редуктора – водило.

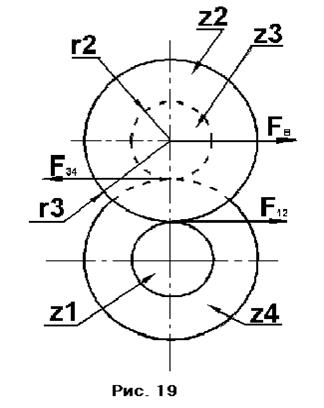
Передаточное отношение планетарного механизма определяется методом обращённого движения (остановки водила). Условно всем звеньям механизма сообщается дополнительное движение с угловой скоростью водила ω_В, но в сторону, противоположную вращению последнего. Кинематическая схема обращённого механизма представлена на рис. 19.

Для каждой из двух планетарных передач можно написать выражение основной формулы планетарной передачи:

(42)

где — передаточные отношения планетарных передач при неподвижном водиле;

ω₁ и ω₂ -- угловые скорости солнечных колёс z₁ и z₄ (ω₄ = 0);

ω_В -- угловая скорость водила.

Угловые скорости берутся с учётом направления вращения.

Учитывая, что ω₂ = ω₃, получим 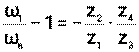(42)

Тогда передаточное отношение планетарного редуктора равно

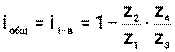(44)

 

Если водило остаётся неподвижным, то планетарный редуктор становится обычной зубчатой передачей с неподвижными осями. Его передаточное отношение равно

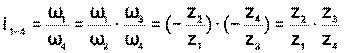(45)

 

Составим уравнение внешних моментов, действующих на планетарный редуктор:

 

(46)

где М₁ – момент солнечного колеса z₁ ;

М₄ -- реактивный момент солнечного колеса z₄ ;

М_В – момент водила.

Коэффициент полезного действия обращённого механизма равен:

,откуда . (47)

Моменты М₁ и М₄ имеют противоположные направления. Заменим в равенстве (47) его выражением из равенства (46)

 

(48)

 

Коэффициент полезного действия планетарного редуктора равен:

(49)

При подсчёте по формуле (49) передаточные отношения планетарного редуктора i_1-В и обращённого механизма определяются по формулам (44) и (45). Коэффициент полезного действия обращённого механизма принимается равным

 

(50)

 

где η_1-2 и η_3-4 -- КПД первой и второй ступеней обращённого механизма, определяемый по формулам (4).

Параметр С для планетарной передачи (эвольвентного зубчатого зацепления) рассчитывается по формуле:

(51)

где F – окружное усилие в зацеплении, измеряемое в Н и определяемое и соотношения

; (52)

d – диаметр делительной окружности соответствующего колеса, равный d = m _* z;

m – модуль зацепления, стандартный параметр (для данного редуктора m = 1 мм);

М – крутящий момент на колесе, Н_*мм.

А параметр по формуле:

 

, (53)

где f — коэффициент трения.

Окружные усилия в зацеплениях можно определить из условия равновесия сил и моментов относительно вала сателлитов 2 (рис.19):

 

(53)

 

(54)

 

где r₂ -- радиус сателлита z₂;

r₃ -- радиус сателлита z₃;

F₁₂ -- окружное усилие в зацеплении колёс z₁ и z₂;

F₃₄ -- окружное усилие в зацеплении колёс z₃ и z₄;

F_B -- окружное усилие на водиле.

(55)

 

Решая совместно уравнения (53) и (54) с учётом выражения (55), находим

 

, (56)

 

; (57)

Задаваясь несколькими значениями момента нагрузки, т. е. момента М_В, определим для каждого значения F₁₂ и F₃₄ по формулам (56) и (57). Затем находим η_1-2 и η_3-4. КПД планетарного редуктора определяем из (49), учитывая (6):

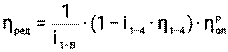, (58)

где η_оп – КПД одной пары подшипников; η_оп = 0, 9;

р – число пар подшипников.

В приводе, содержащем планетарный редуктор, зависимость между моментом на двигателе Мдв, и моментом нагрузки Мн в соответствии с формулой (6) будет иметь вид:

, (59)