(1.6)
Себестоимость является качественным показателем, поэтому соизмерителем берем количественный показатель физического объема (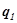
) и обозначение его периода берем по числителю обозначения периода вычисления себестоимости (
) (отношение себестоимости в отчетном периоде 
к базисному 
)
Общий индекс товарооборота.
(1.7)
Общий индекс затрат на производство.
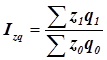(1.8)
Пример. Пусть имеются сведения о ценах и реализации товаров за два периода. Эти данные приведены в табл. 1.
Как видно из табл. 1, совокупность товаров разнородная (единицы измерения). Определим агрегатный индекс цен.
,
т.е. цены возросли в целом на 13,9%. В данном примере цена – индексируемый показатель, а объем - вес, взятый за отчетный период.
Таблица 1.1
Реализация товаров
| Товар | Единица измерения | I период (базисный) | II период (отчетный) | Индивидуальные индексы | |||
Цена за единицу товара, руб., ( )
| Количество товара, ( )
| Цена за единицу товара, руб., ( )
| Количество товара, ()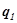
| Цены,
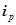
| Физического объема, 
| ||
| А | т | 1,25 | 1,27 | ||||
| Б | м | 1,0 | 1,25 | ||||
| В | шт | 0,67 | 1,5 |
Можно в качестве весов взять объем и за базисный период. Тогда агрегатный индекс цен будет иметь вид:
,
т.е. цены возросли на 14,4 % (114,4-100 = 14,4%).
Для того чтобы по двум известным индексам определить третий неизвестный, в статистике используется взаимосвязь между общими индексами. Индекс реализации продукции (товарооборота) равен произведению общего индекса физического объема на общий индекс цен, а индекс затрат на производство продукции равен произведению общего индекса себестоимости продукции на общий индекс физического объема.
|
|
(1.9)
(1.10)
Средневзвешенный индекс – это средний из индивидуальных индексов, взвешенных на объемы, имеющие одинаковую размерность и зафиксировнные на неизменном уровне.
Средневзвешенный индекс физического объема получают, если преобразования делаются в числителе общего индекса, т.е. в среднеарифметической форме, через соответствующий индивидуальный индекс 
. При этом условный товарооборот 
, т.к. 
.
(1.11)
Средневзвешенный индекс цен получают, если преобразования делаются в знаменателе общего индекса, т.е. в среднегармонической форме.
(1.12)
При этом условный товарооборот 
вычисляется через индивидуальный индекс цен 
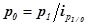, откуда 
, а 
Решите задачи
Задача 1. Себестоимость за одну единицу продукции в базисном периоде составляет 60 руб.,
в отчетном периоде - 70 руб. Рассчитайте индивидуальный индекс себестоимости:
Задача 2.. Цена товара уменьшилась на 3 %. Определите индекс цены:
Задача 3. Выручка фирмы от реализации товара на рынке выросла на 10 % при увеличении объема продажи товара на 22 %. Как изменились цены на товар?
Задача 4. Общие затраты на производство по предприятию увеличились в отчетном периоде по сравнению с базисным периодом на 20 % при увеличении объема производства на 27 %.Как изменилась в отчетном периоде по сравнению с базисным периодом себестоимость единицы продукции?
Задача 5. Товарооборот по молочным продуктам увеличился в июне по сравнению с мартом на 4 %, а цены были снижены за этот же месяц на 15 %.
Как изменилось количество проданных молочных продуктов в июне по сравнению с мартом?
|
|
Задача 6. Оборот в действующих ценах по системе составил за октябрь 59 тыс. руб. Цена на сметану в октябре увеличилась на 10%. Определите оборот в сопоставимых ценах.
Задача 7. Вычислите средний индекс физического объема товарооборота, если:
∑p1 q1 – 560 тыс. руб.
∑p0 q0 – 480 тыс. руб.
∑p0 q1 – 420 тыс. руб.
Дайте экономическое обоснование.
Задача 8. Исчислите сумму экономии (переплаты) населением от снижения цен, если:
∑p1 q1 – 74 тыс. руб.
∑p0 q0 – 68 тыс. руб.
∑p0 q1 – 76 тыс. руб.
Задача 9. Вычислите индивидуальный базисный индекс цен на яблоки за сентябрь месяц.
Цены на яблоки за 1 кг. руб.:
июль август сентябрь
62 65 70
Поясните экономический смысл.