Наработка - это работа изделия от начала эксплуатации до возникновения отказа (авто – км, спецтехника - моточасы).
Закон распределения случайной величины – это дифференциальная функция распределения плотности вероятности отказа f(t). f(t) – вероятность отказа за малую единицу времени при работе ДУА без замены.
Для процессов технической эксплуатации наиболее характерны следующие законы распределения:
1. нормальный закон
2. логарифмически нормальный закон
3. закон распределения Вейбула-Гнеденко
4. экспоненциальный закон
Кроме перечисленных, встречаются и другие законы распределения: гамма-распределение; закон Релея; закон Пуассона,не получившие широкого применения в решении практических задач ТЭА.
Нормальный закон распределения формируется тогда, когда на протекание исследуемого процесса и его результат влияет большое число независимых факторов (слагаемых), каждое из которых в отдельности оказывает лишь незначительное действие по сравнению с суммарным влиянием всех остальных. В этом периоде эксплуатации постепенные отказы ещё не проявляются, и надёжность характеризуетсявнезапными отказами λ(t)=λ=const, λ=1/t.
Например, наработка до проведения ТО складывается из нескольких (десяти и более) сменных пробегов, отличающихся один от другого. Однако влияние одно сменного пробега на суммарную наработку незначительно и поэтому периодичность ТО подчиняется нормальному закону, для которого имеем: Плотность вероятности отказа это вероятность отказа за достаточно малый промежуток наработки ∆Х. 
;
Зная плотность вероятности отказа можно рассчитать вероятность отказа за любой промежуток пробега, то есть можно спланировать количество запчастей, которое потребуется для каждой марки авто по каждому агрегату на предстоящий год. m(x1-x2)≈ n*f(X)*∆X. Например n=75 термостатов, ∆X=4000 км f(42000)=0,2. m(40000-44000) ≈0,2*4*75= 60 отказавших термостатов. Для нормального закона при расчетах часто пользуются понятием нормированной функции Ф(z), для которой принимается новая случайная величина 
так называемое нормируемое отклонение. Тогда: 
|
|
Для нормированной функции составлены таблицы, облегчающие расчеты. Коэффициент вариации для этого закона не превышает 0,33.
ЛОГАРИФМИЧЕСКИ НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ. Если на протекание исследуемого процесса и его результат влияет сравнительно большое число случайных и взаимонезависимых факторов, интенсивность действия которых зависит от достигнутого случайной величиной состояния, то возникают условия для логарифмически нормального закона. Эта так называемая модель пропорционального эффекта рассматривает некоторую случайную величину, имеющую начальное состояние t0 и конечное предельное состояние tn. Изменение случайной величины происходит таким образом, что ti=ti – 1 εi · h(ti – 1)
Где εi – интенсивность изменения случайных величин; h(ti – 1) – функция реакции, показывающая характер изменения случайной величины.
Для такого закона имеем:
Таким образом, предельное состояние
а его логарифм lntn = lnt0 + Σln(1 εi).
ЗАКОН РАСПРЕДЕЛЕНИЯ ВЕЙБУЛА-ГНЕДЕНКО Закон проявляется в модели так называемого «слабого звена». Если система состоит из группы независимых элементов, отказ каждого из которых приводит к отказу всей системы, то в такой модели рассматривается распределение времени (или пробега) достижения предельного состояния системы как распределение соответствующих минимальных значении ti отдельных элементов: tc = min (t1, t2… tn). Функция распределения этой величины может быть выражена следующей зависимостью:
|
|
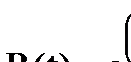
где а и b – параметры распределения.
ЭКСПОНЕНЦИАЛЬНЫЙ ЗАКОН является однопараметрическим, что облегчает расчеты и объясняет широкое распространение данного закона.
Вероятность безотказной работы при таком законе распределения ресурса до отказа имеет вид:
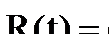где λ – параметр потока отказов или интенсивность отказов, равный обратной величине средней наработке на отказ 
.
Плотность распределения тогда 
Знание законов распределения случайных величин позволяет более точно планировать моменты и трудоемкость работ ТО и ремонта, определять необходимое количество запасных частей и решать другие технологические и организационные вопросы.
Нормальный закон распределения может применятся для определения количества автомобилей потребующих замены или ремонта ДУА на определенном этапе наработки.
Для определения закона распределения наработки до отказа необходимы статистические данные о неисправностях ДУА у исследуемых машин.
С этой целью на предприятии случайным образом из общего числа автомобилей одной марки, надежность которых изучается, отбирается группа машин, называемых выборкой. Выборка нужна для облегчения сбора информации о поведении ДУА, так как по разным причинам порой бывает трудно или даже невозможно, отследить за поведением изучаемого объекта на всех машинах.
|
|
Выборку представляет собой транспорт одной модели и марки, надежность которой изучается, причем, чем ближе друг к другу условия, в которых эксплуатируются автомобили, и чем ближе число машин в выборке к общему числу автомобилей данной модели, тем с большей уверенностью можно говорить о надежности всего парка данной марки по их поведению в выборке.