Задачи для самостоятельной работы студентов

Зинковская Е.В.,

Расчет надежности машин и оборудования: Практикум по дисциплине «Надежность машин» / Башк. гос. ун-т; Сост.: Е.В.Зинковская- Уфа, 2017. - 32 с.

Практикум проводится с целью закрепления и конкретизации пройденного теоретического материала и овладения новыми методами и методиками исследования количественных и качественных зависимостей между величинами и параметрами, характеризующих надежность машин и оборудовния.

Практикум предназначен для студентов, обучающихся по направлению 150302 «Технологические машины и оборудование», изучающих дисциплину «Надежность машин».

 

©Зинковская Е.В.,

©Баш ГУ

 

СОДЕРЖАНИЕ

Введение......................................................................................... 4

Практическое занятие №1................................................................ 5

1.1. Цель практического занятия.................................................... 5

1.2. Задачи практического занятия................................................ 5

1.3. Краткие теоретические сведения и задачи

для практического решения............................................................. 5

1.4. Задачи для самостоятельной работы студентов....................... 11

Практическое занятие № 2............................................................. 13

2.1. Цель практического занятия.................................................. 13

2.2. Задачи практического занятия............................................... 13

2.3. Краткие теоретические сведения и практические задачи........ 13

2.4. Задачи для самостоятельной работы студентов....................... 16

Практическое занятие № 3............................................................. 19

3.1. Цель практического занятия.................................................. 19

3.2. Задачи практического занятия............................................... 19

3.3. Краткие теоретические сведения и задачи для

практического решения................................................................. 19

3.4. Задачи для самостоятельной работы студентов....................... 25

Требования к содержанию и оформлению

отчета о решении задач................................................................. 26

Критерии результативности практикума........................................ 26

Список литературы........................................................................ 28

Приложение А.............................................................................. 29

Приложение Б..................................................................................... 30

 

 

ВВЕДЕНИЕ

Практикум предназначен для проведения аудиторных занятий по дисциплине:«Надежность машин».

Решение практических задач является важнейшим этапом в освоении теории надежности машин и оборудования.

Практикум проводится с целью закрепления и конкретизации пройденного теоретического материала и овладения новыми методами и методиками исследования количественных и качественных зависимостей между величинами и параметрами, характеризующих

надежность электрооборудования электроэнергетических систем.

Выполнение практических занятий позволит студентам: изучить методы расчета надежности элементов машин и оборудования; продемонстрировать знания и умения решения практических задач, основанных на классической теории вероятности, теории планирования эксперимента в области расчета надежности технических систем; освоить методологические принципы формализации задач по расчету надежности машин и оборудования; закрепить, полученные на аудиторных занятиях знания.

Каждая тема практикума начинается с освещения общей теоретической концепции рассматриваемой проблемы, затем приводятся примеры решения и предлагаемые для решения аудиторном занятии задачи, далее приводятся задачи для самостоятельного решения. В приложениях дан необходимый справочный и статистический материал.

Данный практикум полностью коррелируется с учебным пособием [1] и методическими указаниями к курсовому проектированию [2], пояснения к терминам и определениям, используемым в данном практикуме, даны в [3, 4]. В совокупности эти учебно-методические труды представляют собой единый обучающий комплекс.

 

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1

 

ВЕРОЯТНОСТНЫЕ МЕТОДЫКОНТРОЛЯ И ОЦЕНКИ
НАДЕЖНОСТИ МАШИН И ОБОРУДОВАНИЯ

1.1. Цель практического занятия

Овладение вероятностными методами контроля и оценки надежности машин и оборудования.

1.2. Задачи практического занятия

Закрепление, углубление и расширение знаний студентов при решении конкретных практических задач контроля и оценки надежности машин и оборудования.

1.3. Краткие теоретические сведения и задачи для практического решения

С проблемой надежности в машиностроении связаны следующие практические задачи: статистическая оценка и анализ надежности действующего оборудования и установок; прогнозирование надежности оборудования и установок; нормирование уровня надежности; испытания на надежность; расчет и анализ надежности; оптимизация технических решений по обеспечению надежности при проектировании, создании и эксплуатации электротехнического оборудования, установок, систем. Теория надежности вводит в практику инженерного исследования количественные оценки, которые позволяют: устанавливать

требования и нормативы надежности оборудования для установок и систем; сравнивать различные виды оборудования, установок и систем по их надежности; рассчитывать надежность установок по надежности их элементов; оптимизировать величину необходимого резерва и структуру технических объектов; выявлять наименее надежные элементы оборудования, установок и систем; оценивать сроки службы оборудования и установок.

Проблема анализа и расчета надежности машин и оборудования связана с решением ряда теоретических и практических задач. Для этого необходимо: выбрать меру надёжности; дать математическое описание явлений, связанных с ненадежной работой оборудования и всей установки или системы в целом; разработать математическую модель взаимосвязи отдельных явлений, определяющих возникновение повреждений и нарушений работы установки и ее восстановление, как случайный процесс; дать предложения по учету надежности в моделях принятия технических решений в проектных и эксплуатационных задачах.

Задача 1.1 В результате статистического исследования надежности синхронных генераторов типа ЕС мощностью до 100 кВт получены данные за период с 2007 по 2012 г. Распределение отказов по основным узлам машин следующее: обмотка ротора - 26. обмотка статора - 22, блок регулирования напряжения — 188, подшипниковый узел — 21, контактно-щеточный узел - 72. Определить статистическую вероятность отказа каждого из перечисленных узлов.

Решение. Общее число зафиксированных отказов:

n = 26 + 22 + 188 + 21 + 72 = 329.

Статистическая вероятность отказов соответственно: обмотки ротора:

Здесь 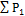= 1.

Задача 1.2 В партии из N деталей для выключателей имеются п стандартных. Случайным образом отобрано М деталей. Найти вероятность того, что среди отобранных деталей ровно т стандартных.

Решение. Общее число возможных исходов испытаний равно числу способов, которыми можно выбрать М деталей из партии N деталей, т.е. C_N — числу сочетаний из N элементов по М. Рассчитаем число исходов, благоприятствующих событию - среди Мдеталей ровно т стандартных: т стандартных деталей можно взять из п стандартных деталей С„ способами; при этом остальные (М-п) деталей должны быть нестандартными; взять же (М-т) нестандартных деталей из (N-п) нестандартных деталей можно способами. Следовательно, число благоприятствующих исходов равно .Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех исходов:

Задача 1.3 При входном контроле из 200 испытанных образцов проводов оказались пробитыми 18. Какова статистическая вероятность пробоя?

Задача 1.4 В партии 100 выключателей, из них 10 бракованных. При контроле произвольно взяты четыре выключателя. Найти вероятность того, что среди этих четырех выключателей: а) нет бракованных; б) нет годных.

Задача 1.5 В контейнере 10 одинаковых изоляторов с номерами 1,2,...,10. Произвольно взяты шесть изоляторов. Найти вероятность того, что среди извлеченных изоляторов окажутся: а) изолятор № 1; б) изоляторы № 1 и № 2.

Задача 1.6 Пускорегулирующее устройство состоит из пяти элементов, из которых два изношенные. При включении устройства случайным образом включаются два элемента. Найти вероятность того, что включенными окажутся изношенные элементы?

Задача 1.7 При приемке партии из 80 рубильников, среди которых шесть бракованных, проверяются 40 случайным образом выбранных изделий.

Определить вероятность того, что партия будет принята, если условиями приема допускается не более двух бракованных изделий среди проверенных.

Решение. Обозначим: А - событие, состоящее в том, что при проверке 40 изделий не получено ни одного бракованного изделия;

В — событие, состоящее в том. что получено только одно бракованное изделие, и С - событие, состоящее в том, что получено два бракованных изделия.

События A, В и С несовместны.

Партия изделий будет принята, если имеет место

событие (A + В + С). Поэтому по теореме сложения вероятностей искомая вероятность

Р = Р{А+ В + С) = Р{А) + Р(В)+ Р(С).

Из 80 изделий 40 изделий можно выбрать , способами. Из 74 набракованных изделий 40 можно выбрать способами. Следовательно, P(a) = / , Р(в) = / и

Р(С) = 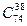/ . ОтсюдаP = Р(А) + Р(В) + Р(с) 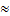0,337.

Задача 1.8 При приемке партии из 120 автоматических выключателей, среди которых семь бракованных, проверяются случайным образом шестьдесят выключателей. Определить вероятность того, что партия будет принята, если условиями приема допускается не более трех бракованных изделий среди проверенных.

Задача 1.9 На складе имеется 15 упакованных гирлянд изоляторов на напряжение 35 кВ, причём пять из них фарфоровых, остальные стеклянные. Электромонтёр берёт наудачу 3 гирлянды. Найти вероятность того, что хотя бы одна из взятых гирлянд окажется изготовленной из фарфора.

Задача 1.10 Для сигнализации об аварии генератора установлено два независимо работающих сигнализатора. Вероятность того, что сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для второго. Найти вероятность того, что при аварии сработает только один сигнализатор.

Задача 1.11 Изоляция паза состоит из двух слоев. Вероятность пробоя первого слоя равна 0.9; вероятность пробоя второго слоя - 0,95. Какова вероятность пробоя только одного слоя?

Задача 1.12 Вероятность того, что при одном измерении параметра силового трансформатора будет допущена ошибка, превышающая заданную точность, равна 0,4. Произведено три независимых измерения. Найти вероятность того, что только в одном из них допущенная ошибка превысит заданную точность.

Задача 1.13 Устройство защиты состоит из трех элементов, работающих независимо. Вероятности безотказной работы за время t первого, второго и третьего элементов соответственно равны 0,6, 0,7 и 0,8. Найти вероятность того, что за время t безотказно будут работать: а) только один элемент; б) только два элемента; в) все три элемента.

Задача 1.14 Три группы станков производят одни и те же детали, но качество деталей различно. Станки первой группы производят 94 % стандартных деталей; второй группы — 90 %, третьей группы — 85 %. Все детали отправлены на выборочный контроль. Определить вероятность того, что произвольно взятая деталь будет соответствовать требованиям стандарта, если число станков первой группы равно пяти, второй - трем, третьей - двум.

Решение. Событие А — проверенная деталь соответствует требованиям стандарта. Гипотезы: H₁ — эта деталь со станков первой группы; Н₂ - второй группы; Н₃- третьей группы. Вероятность каждой гипотезы: Р(Н₁) = 0,5; Р(Н₂) = 0,3; Р(Н₃) = 0.2.

Условные вероятности при этих гипотезах: Р(А/Н₁) = 0,94 Р(А/Н₂) = 0,9; P(А/Н₃)- 0,85. Вероятность события А: Р(А) = 0.5 0,94 + 0.3 0,9 + 0,2 0.85 = 0,91.

Задача 1.15 Два из трех независимо работающих элементов пускорегулирующей аппаратуры отказали. Найти вероятность того, что отказали первый и второй элементы, если вероятность отказа первого, второго и третьего элементов равны 0,2; 0,4 и 0,3.

Решение. Обозначим через А событие: отказали два элемента. Можно выдвинуть гипотезы: B₁ - отказали первый и второй элементы, третий элемент исправен. Тогда

Р(В₁) = p₁p₂q₃ = 0,2 0,4 0,7 = 0,056,

В₂ — отказали первый и третий элементы, второй элемент исправен.

Тогда

Р(В₂) = p₁p₂q₂ = 0.2 0.3 0.6 = 0.036;

В₃ — отказали второй и третий элементы, первый исправен, причем Р(В₃)= p₁p₃q₁, = 0,4 0,3 0,8 = 0,096,

где q₁ = 1 - р₁, q₂ = 1 - р₂, q₃ = 1 - р₃. В₄ - отказал один элемент;

В₅ - отказали все три элемента; В₆ — ни один из элементов не отказал.

Вероятности последних трех гипотез не вычислены, так как при этих Вероятности последних трех гипотез не вычислены, так как при этих гипотезах событие А (отказали два элемента) невозможно.

Поскольку при гипотезах В₁,В₂,В₃ событие А достоверно, то соответствующие условные вероятности равны единице: Р(А/В₁) = P(A/B₂) = Р(А/В₃) = 1.

В соответствии с формулой полной вероятности

р(а)=Р(В₁)(А/В₁)+P(B₂)(A/B₂) + P(B₃)(A/B₃)

Р(а) = 1 0,056 + 1 0,036 + 1 0,096 = 0,188.

В соответствии с формулой Бейеса, вероятность того, что отказали первый и второй элементы, равна

Р(B₁ /А) = Р(В₁)(А/В₁)/ Р(A)=0,056/ 0,188 = 0,3.

Задача 1.16 Два станка производят одинаковые детали, которые поступают на общий конвейер. Производительность первого станка вдвое больше производительности второго. Первый станок производит в среднем 60 % деталей отличного качества, а второй - 84 %. Случайным образом взятая с конвейера деталь оказалась отличного качества. Какова вероятность того, что эта деталь изготовлена первым станком?

Решение. Обозначим через А событие, состоящее в том, что взятая деталь - отличного качества. Считаем B₁ - деталь сделана первым станком, причем P(В₁) = 2/3, так как первый станок вдвое производительней второго; В₂ - деталь сделана вторым станком, причем Р(В₂) = 1/ 3. В соответствии с условием Р(А/ В₁) = 0,6 P(A/B₂) = 0,84. По формуле Бейеса искомая вероятность Р(В₁ /А) =P(B₁)/(A/B₁)/P(A) = 2/ 3 0,6 /(2 /3 0,6 +1/3 0,84) = 0,588.

Задача 1.17 В трех ящиках находятся однотипные изделия: в первом 10 изоляторов, из них три нестандартные; во втором - 15, из них пять нестандартные; в третьем 20, из них шесть нестандартные. Изделия перемешаны и предъявлены на контроль, одно из них оказалось нестандартным. Какова вероятность того, что это изделие находилось во втором ящике?

Задача 1.18 Известно, что 95% выпускаемых выключателей удовлетворяет требованиям стандарта. По упрощенной схеме контроля признается пригодной стандартная продукция с вероятностью 0,98 и нестандартная с вероятностью 0,06.

Определить вероятность того, что выключатели, прошедшее упрощенный контроль, удовлетворяет требованиям стандарта.

Задача 1.19 Вероятности того, что при работе ЭВМ произойдет сбой в считывающем устройстве, в оперативной памяти, в других устройствах, относятся как 3:2:5. Вероятности обнаружения сбоя в этих устройствах соответственно равны 0,8; 0,9; 0,9. Найти вероятность того, что возникший в ЭВМ сбой произошел в считывающем устройстве.

Задача 1.20 В специализированную мастерскую поступают в среднем 50% вышедших из строя масляных выключателей с повреждением дугогасительной камеры (ДГК), 30%— с повреждением блока управления, 20% - с повреждением корпуса. Вероятность дальнейшего использования выключателей с повреждением ДГК равна 0,7; для блока управления и корпуса соответственно равны 0,8 и 0,9. Повреждённый выключатель был успешно отремонтирован. Найти вероятность того, что этот выключатель имел повреждение ДГК.

Задача 1.21 В щеточном узле 10 щеток. Узел считается работоспособным, если пригодны не менее девяти щеток. Какова вероятность безотказной работы щеточного узла, если вероятность безотказной работы щетки за время t равна 0,9?

Решение. Щеточный узел работоспособен, если работоспособны все 10 щеток из 10-P_10,l0 и девять щеток из 10 - Р_{9, 10}. Тогда в соответствии с (1.14) и теоремой сложения вероятностей:

Р = = 0,7361.

Напомним, что 0!=1.

Задача 1.22 Испытывается каждая из 15 секций машины. Вероятность того, что секция выдержит испытания, равна 0,9. Найти наивероятнейшее число секций, которые выдержат испытания.

Решение. По условию n = 15; p = 0,9; q = 0,1 в соответствии с (1.15) получим: 13,5 <k₀ <14,4. Отсюда k₀ = 14.

Задача 1.23 Согласно методу «слабых звеньев» синхронная машина представлена в виде трех узлов: 1 -й - контактные кольца, 2-й - подшипниковый узел, 3-й - обмотка якоря, причем вероятность безотказной работы за 1500 ч р, = 0.7; р₂ = 0,8; р₃ = 0.9. Проводятся испытания на надежность. Найти вероятность того, что за 1500 ч будут работать безотказно: а) все узлы; б) два узла; в) один узел; г) ни один из узлов; д) хотя бы один узел.

Решение. Вероятности безотказной работы и вероятности отказов соответственно равны:p₁=0.7; p₂=0,8; p₃=0,9 и q₁ = 0,3; q₂ = 0,2; q₃= 0,1. Составим производящую функцию:

y_n(x) = (р₁х +q₁) (p₂x+ q₂) (p₃x + q₃) =

= (0,7х + 0,3) (0,8х + 0,2) (0,9х + 0.1) =

= 0,504х3 + 0,398х2 + 0,092х + 0,006.

Вероятность того, что все три узла будут работать безотказно, равна коэффициенту при х³, т.е. Р₃(3) = 0,504.

Вероятность того, что безотказно будут работать два узла (коэффициент при х²) Р₂(3) = 0,398. Вероятность того, что будет работать один узел P₁ (3) = 0,092.

Вероятность того, что ни один из узлов не будет работать (коэффициент при х° = 1, т.е. при свободном члене) равна P₀(3) = 0.006. Вероятность того, что будет работать хотя бы один узел — событие, противоположное событию, когда не работает ни один узел. Значит P_1,2,3(3) = 1-Р₀(3) = 1-0.006 = 0.994.

Задача 1.24 Последовательно посланы четыре сигнала. Вероятность фиксации каждого из них не зависит от того, приняты ли остальные сигналы, и соответственно равна 0,2; 0,3; 0,4; 0,5. Определить вероятность фиксации трех сигналов.

Задача 1.25 При данном технологическом процессе 85% всей производимой продукции высшего качества. Найти наивероятнейшее число изделий высшего качества в партии из 150 изделий.

Задачи для самостоятельной работы студентов

Задача 1.26 Определить наиболее вероятное число вышедших из строя приборов (в целях создания необходимого комплектного запаса) в системе из 13 приборов, если отказ одного прибора независим и вероятность отказа одного прибора в год равна 4/7.

Задача 1.27 Чему равна вероятность Р наступления события в каждом из 39 независимых испытаний, если наивероятнейшее число наступления события в этих испытаниях равно 25?

Задача 1.28 Производится шесть попыток закрепления опор ВЛ. Из опыта известно, что вероятность закрепления одной точки конструкции равна 0,3.

Найти: а) наивероятнейшее число точек закрепления;

б) вероятность наивероятнейшего числа точек закрепления;

в) вероятность того, что конструкция будет закреплена, если для этого необходимо не менее двух точек закрепления.

Задача 1.29 Определить наиболее вероятное число вышедших из строя батарей конденсаторов — БК (в целях создания необходимого комплектного запаса) в системе из 13 БК, если отказ одной БК независим и вероятность отказа одной БК в год равна 4/7.

 

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 2

ЗАКОНЫРАСПРЕДЕЛЕНИЯ ДИСКРЕТНЫХ СЛУЧАЙНЫХ

ВЕЛИЧИН

2.1. Цель практического занятия

Закрепление пройденного теоретического материала и овладение методиками исследования законов распределения дискретных случайных величин.

2.2. Задачи практического занятия

Закрепление, углубление и расширение знаний студентов при решении конкретных практических задач методиками исследования законов распределения дискретных случайных величин.

2.3. Краткие теоретические сведения и практические задачи

Случайной называется величина, которая в результате испытаний может принять то ши иное значение, причем заранее неизвестно, какое именно.

Случайные величины могут быть дискретными и непрерывными. Непрерывными случайными величинами являются: время безотказной работы элементов, устройств, агрегатов, систем; время вынужденного простоя оборудования из-за отказов; уровень того или иного технического параметра и т.д. Дискретными случайными величинами являются: число неисправных элементов, устройств, агрегатов из общего числа находящихся в эксплуатации; число дефектных изделий в какой-либо партии продукции; количество повреждений элементов какого-либо оборудования в единицу времени и т.д.

Из-за невозможности указать, какое конкретное значение примет случайная величина в данном эксперименте, для ее характеристики применяются вероятности того, что она будет равна заданному значению или окажется в указанных пределах возможного значения.

При этом используются понятия числовых характеристик распределений случайных величин.

Основные числовые характеристики случайных величин — математическое ожидание {среднее значение), дисперсия, среднее квадратическое отклонение, мода, медиана, коэффициент вариации.

Задача 2.1 Блок управления состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте.

Решение. Число отказавших элементов в одном опыте может принимать следующие значения: х₁=0 (ни одного отказа), х₂ = 1, х₃ =2, х₄=3. Отказы независимы, вероятность отказов постоянна, поэтому применима формула Бернулли.

Учитывая, что р = 0,1; q = 1; р₂=0,9 и п=3, получим: Р₃(0) = q³ =0.729; P₃(l) = С p²q= 0,027; Р₃(3) = р³ =0.001.

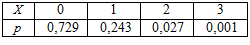Искомый биномиальный закон распределения:

Задача 2.2 На завод поступила партия подшипников из 100000 шт. Вероятность того, что подшипник бракованный, равна 0,0001. Найти вероятность того, что в партии будет ровно пять бракованных подшипников.

Решение. По условию n = 100000, р = 0,0001, k = 5. События независимы, число п велико, а вероятность р мала, поэтому следует использовать распределение Пуассона (2.2). Найдем = пр = 100 000 0,0001 = 10. Отсюда Р_5,100000 =10⁵е^-10/5!= 0,0375.

Задача 2.3 Среднее число отказов двигателей на поточной линии за месяц равно трем. Найти вероятность того, что за два месяца произойдет: а) четыре отказа; б) менее четырех отказов; в) не менее четырех отказов.

Решение. По условию = 3, t = 2, k = 4. По формуле Пуассона (1.18), искомая вероятность того, что за два месяца произойдет четыре отказа P₂(4) = 6⁴е^-4/4!= 0,135. Событие «менее четырех отказов» произойдет, если произошло три отказа, или два отказа, или один отказ, или ни одного отказа. Эти события несовместны, поэтому в соответствии с теоремой сложения (1.8):

P₂(k<4)=P₂(3)+P₂(2)+P₂(1) + P₂(0) =

= 6³е^-6/3!+6²е^-6/2!+6¹е^-6/1!+6⁰е^-6/0! = 0.1525

События «менее четырех отказов» и «не менее четырех отказов» противоположны, поэтому искомая вероятность того, что за два месяца произойдет не менее четырех отказов: P(k > 4)= 1 — Р(k < 4)= 0.

Задача 2.4 Случайная величина X представляет собой число бракованных выключателей из возвратной выборки в 50 штук. Вероятность брака одной детали р = 0,06.

Найти математическое ожидание. дисперсию и среднеквадратическое отклонение числа бракованных выключателей в выборке.

Решение. Случайная величина X имеет биномиальное распределение. Поэтому математическое ожидание M[X] = пр = 50 0,06 = 3. Дисперсия и среднеквадратическое отклонение D(x) = npq = 50 0,06 (l - 0,06) =2,82;

(х)= 1.68.

Задача 2.5 В группе из 10 изделий имеется одно бракованное. Чтобы его обнаружить, выбирают одно изделие за другим и каждое проверяют. Пусть X - число проверенных изделий, включая бракованное. Найти закон распределения, среднее значение и дисперсию случайной величины X.

Задача 2.6 Завод выпускает 96% изделий первого сорта и 4% изделий второго сорта. Случайным образом отбирают 1000 изделий. Пусть X — число изделий первого сорта в данной выборке. Найти среднее значение и дисперсию случайной величины X.

Задача 2.7 Производится проверка пазовой изоляции двигателя на пробой до первого пробоя. Испытания независимые. Априори известно, что вероятность пробоя равна р. Построить ряд распределения числа произведенных испытаний. Найти математическое ожидание и среднеквадратическое отклонение числа испытаний.

Задача 2.8 В партии из 10 деталей имеется восемь стандартных. Случайным образом отобраны две детали. Составить закон распределения числа стандартных деталей среди отобранных (заметим, что рассматриваемый закон называется гипергеометрическим).

X
р	1/45	16/45	28/45

Решение. Случайная величина X - число стандартных деталей среди отобранных деталей - имеет следующие возможные значения: x₁=0; х₂ = 1; х₃=2. Найдем соответствующие вероятности (см. аналогичную задачу 1.2): P(X =0) = = 1/45; P(Х = 1) = 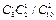= 16/45; Р(Х = 2)= 26/45.Составим закон распределения:

Запишем общую формулу гипергеометрического закона

Р(X = k) = 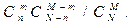(2.9)

где N — число деталей в партии; п - число стандартных деталей; М- число отобранных деталей; т - число стандартных деталей среди отобранных.

Задача 2.10 На пульт управления энергоблоком в течение определенного часа дня поступает в среднем 30 сигналов от датчиков. Найти вероятность того, что в течение минуты поступают не более двух вызовов.

Задача 2.11 Математическое ожидание числа отказов системы автоматического управления генератором за 1000 ч работы равно пяти. Определить вероятность отказа системы автоматики за 20 ч работы.

Задача 2.12 Обмотка статора представлена как 500 элементарных участков. Вероятность пробоя одного участка за год равна 0,01. Какова вероятность того, что в течение года произойдет три пробоя?

Задача 2.13 Завод отправил на базу 500 двигателей. Вероятность повреждения двигателя в пути равна 0,002. Определить вероятность того, что в пути будет повреждено двигателей: а) ровно три; б) менее трех; в) более трех.

Задача 2.14 Летняя сессия студента Гены Зубрилова выдалась очень жаркой (+30°С) и длиной (пять экзаменов), так что подготовить он успел только 3/4 билетов по каждому предмету.

Какова вероятность, что его отчислят сразу после сессии и даже не допустят к пересдаче? Каков будет ответ на поставленный вопрос если к первому экзамену Гена подготовил 90 % билетов, ко второму - 85 %, к третьему - 80%, к четвертому - 75% и к пятому - 70 %.

Задача 2.15 В секции «Электроэнергетика» научно-технической конференции участвуют 3 девушки, 4 юноши и руководитель секции. Докладчика решили выбрать случайным образом из 8 человек. Какова вероятность того, что в течение работы (6 дней) 4 раза доклад будут проводить девушки, 5 раз юноши и 2 раза руководитель.