Логарифмом  числа
числа  при основании
при основании  называют показатель степени, в которую нужно возвести основание
называют показатель степени, в которую нужно возвести основание  , чтобы получить
, чтобы получить  :
:  , следовательно
, следовательно  .
.
При любых  любых
любых  и любом
и любом  имеют место следующие равенства:
имеют место следующие равенства:

1.1. 
1.2. 

1.3. 
1.4. 
1.5. 
1.6. 
1.7. 
1.8. 
Логарифмы по основанию 10 называются десятичными (обозначение:  ), а по основанию
), а по основанию  - натуральными (обозначение
- натуральными (обозначение  ). При этом
). При этом 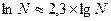 .
.
Приложение 2.
 |





Тригонометрические формулы
 » 3, 14159…, где l - длина окружности, d- диаметр.
» 3, 14159…, где l - длина окружности, d- диаметр.
1. Знаки тригонометрических функций

sina cosa tga, ctga
2. Основные формулы тригонометрии
2.1 Основные соотношения
sin2a+cos2a=1, tga=  , ctga=
, ctga=  , tga×ctga=1;
, tga×ctga=1;  =1+tg2a,
=1+tg2a,  =1+ctga.
=1+ctga.
2.2 Выражение одних тригонометрических функций через другие:

2.3 Свойства дополнительных углов:

2.4 Формулы суммы и разности углов:

2.5 Формулы двойных углов:

2.6 Формулы половинных углов:

Примечание: знаки «+» или «-» определяются по п.1.
2.7 Формулы преобразования суммы в произведение:


2.8 Формулы преобразования произведений в суммы

Приложение 3
3.1 Арифметическая прогрессия есть последовательность чисел ( ) в которой разность (q) двух любых последовательных чисел («последующее» минус «предыдущее») есть величина постоянная. Эта величина называется разностью прогрессии.
) в которой разность (q) двух любых последовательных чисел («последующее» минус «предыдущее») есть величина постоянная. Эта величина называется разностью прогрессии.


3.2 Геометрическая прогрессия есть последовательность чисел ( ) в которой отношение (d) двух последовательных чисел есть величина постоянная. Эта величина q называется знаменателем прогрессии.
) в которой отношение (d) двух последовательных чисел есть величина постоянная. Эта величина q называется знаменателем прогрессии.

 (если прогрессия возрастающая)
(если прогрессия возрастающая)
 (если прогрессия убывающая)
(если прогрессия убывающая)
 (если прогрессия является бесконечно убывающей)
(если прогрессия является бесконечно убывающей)
Приложение 4
4.1 Формулы сокращённого умножения и разложения на множители.

4.2 Формулы решений квадратных уравнений
1)  где
где 
2) 
3) 
4) 
5) Теорема Виета для уравнения 

4.3 Разложение трёхчлена 2-ой степени на множители:
 , где
, где  - корни квадратного уравнения.
- корни квадратного уравнения.
Приложение 5
Некоторые замечательные пределы
1.  ; ;
| 2.  ; ;
| 3. 
|
4.  ; ;
| 5. 
| 6. 
|
7. 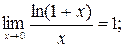
| 8. 
| 9. 
|
Приложение 6
6.1 Основные правила дифференцирования
а) 
б) 
в) 
г) 
д) 
Здесь с=const, u, v и w- дифференцируемые функции.
6.2 Таблица производных.
Пусть  - дифференцируемая функция от переменной х.
- дифференцируемая функция от переменной х.
1. 

2. 

3. 

4. 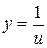

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

16. 

17. 

Приложение 7
7.1 Свойства неопределённого интеграла
1. 
2. 
3.  или
или 
4.  или
или 
7.2 Таблица основных интегралов
1.  ; ;
| 8.  ; ;
|
2.  ; ;
| 9.  ; ;
|
3.  ; ;
| 10.  ; ;
|
4.  ; ;
| 11.  = =
 ; ;
|
5.  ; ;
| 12. 
 ; ;
|
6.  ; ;
| 13.  ; ;
|
7. 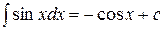 ; ;
| 14.  . .
|
7.3 Простейшие свойства определённого интеграла
1. 
2. 
3. 
4. 
5. 
Задания для контрольной работы
I. Найти указанные пределы, не пользуясь средствами дифференциального исчисления.
1. а)  ; б)
; б) 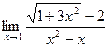 ; в)
; в)  ;
;
г)  .
.
2. а)  ; б)
; б)  ; в)
; в)  ;
;
г)  .
.
3. а)  ; б)
; б)  ; в)
; в)  ;
;
г)  .
.
4. а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
5. а)  ; б)
; б)  ; в)
; в)  ;
;
г)  .
.
6. а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
7. а)  ; б)
; б)  ; в)
; в)  ;
;
г)  .
.
8. а)  ; б)
; б)  ; в)
; в)  ;
;
г)  .
.
9. а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
10. а)  ; б)
; б)  ; в)
; в)  ;
;
г)  .
.
II. Исследовать функцию  на непрерывность: найти точки разрыва функции и определить их тип. Построить схематический график функции.
на непрерывность: найти точки разрыва функции и определить их тип. Построить схематический график функции.
1. 

 2.
2.  3.
3. 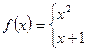


4.  5.
5.  6.
6. 

 7.
7.  8.
8. 

 9.
9. 


10. 

III. Требуется построить по точкам график функции  в полярной системе координат. Найти уравнение этой кривой в прямоугольной системе координат, начало которой совмещено с полюсом, а положительная полуось
в полярной системе координат. Найти уравнение этой кривой в прямоугольной системе координат, начало которой совмещено с полюсом, а положительная полуось  - с полярной осью. Если не указано название кривой, то, по возможности, определить его.
- с полярной осью. Если не указано название кривой, то, по возможности, определить его.
1.  - логарифмическая спираль - логарифмическая спираль
|
2.  - гиперболическая спираль - гиперболическая спираль
|
3. 
|
4. 
|
5.  - трехлепестковая роза - трехлепестковая роза
|
6.  - кардиоида - кардиоида
|
7.  - лемниската - лемниската
|
8. 
|
9. 
|
10. 
|
IV. Найти производные первого порядка данных функций, используя в п. в) логарифмическую производную, в задании д) найти производную обратной функции или функции заданной параметрами.
1. а)  ; б) y = sin(3x + 1);
; б) y = sin(3x + 1);
в)  ; г) 2х – 3у + 1 = 0;
; г) 2х – 3у + 1 = 0;
д) найти  , если у = 3х + х2.
, если у = 3х + х2.
2. а) 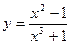 ; б) у = (1 + 2х8);
; б) у = (1 + 2х8);
в)  ; г)
; г)  ;
;
д)  .
.
3. а)  ; б) у = sin(x + sinx);
; б) у = sin(x + sinx);
в)  ; г)
; г)  ;
;
д) найти  , если у = 2х2 + х.
, если у = 2х2 + х.
4. а)  ; б) у = 5cos(2 – 3x);
; б) у = 5cos(2 – 3x);
в)  ; г)
; г)  ;
;
д)  .
.
5. а)  ; б) у = ctg(xsinx);
; б) у = ctg(xsinx);
в)  ; г)
; г)  ;
;
д) найти  , если
, если  .
.
6. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  .
.
7. а)  ; б) y = tg(3x + 1)3;
; б) y = tg(3x + 1)3;
в)  ; г) х2 + у2 = 1;
; г) х2 + у2 = 1;
д) найти  , если
, если  .
.
8. а)  б)
б)  ;
;
в)  ; г) у2 = 4х;
; г) у2 = 4х;
д)  .
.
9. а)  ; б)
; б)  ;
;
в) у = хх; г) х = у + siny;
д) найти  , если
, если  .
.
10.а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  .
.
V. Даны функция z = f(x,y), точка  и вектор
и вектор  . Найти:
. Найти:
- gradZ в точке А;
- производную в точке А по направлению вектора А.
1.  ; А (1,1), а (2,-1).
; А (1,1), а (2,-1).
2.  ; А (2,1), а (3,-4).
; А (2,1), а (3,-4).
3.  ; А (1,1), а (3,2).
; А (1,1), а (3,2).
4.  ; А (1,1), а (2,-1).
; А (1,1), а (2,-1).
5.  ; А (2,1), а (1,2).
; А (2,1), а (1,2).
6.  ; А (2,3), а (4,-3).
; А (2,3), а (4,-3).
7.  ; А (1,2), а (5,-12).
; А (1,2), а (5,-12).
8.  ; А (1,3), а (2,-1).
; А (1,3), а (2,-1).
9.  ; А (-1,2), а (4,-3).
; А (-1,2), а (4,-3).
10.  ; А (1,1), а (2,1).
; А (1,1), а (2,1).
VI. Вычислить следующие неопределённые интегралы:
| 1. | 
| 
| 
|
| 2. | 
| 
| 
|
| 3. | 
| 
| 
|
| 4. | 
| 
| 
|
| 5. | 
| 
| 
|
| 6. | 
| 
| 
|
| 7. | 
| 
| 
|
| 8. | 
| 
| 
|
| 9. | 
| 
| 
|
| 10. | 
| 
| 
|