Зависимости между координатами точек предметной и картинной плоскостей

Примем на картинной плоскости Р за начало координат главную точку схода снимка I, за ось абсцисс - линию действительного горизонта h_i h_i, за ординат - главную вертикаль uV (рис.27).

На предметной плос­кости Е за начало ко­ординат примем главную точку схода I', за ось абсцисс - линию парал­лельную линии действи­тельного горизонта h_i h_i, за ось орди­нат - линию направления съем­ки uV.

Найдем координаты точки А предметной плоскости Е.

В соответствии с рис

Из подобных треугольников 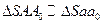можно записать отношение

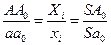(40)

Треугольники и также подобны, следовательно

(41)

где .

Так как отношение принадлежит как уравнению (40), так и уравнению (41), то их можно приравнять, то есть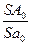

, следовательно

(42)

Вернемся к отношению (41)

, отсюда

. (43)

Мы получили формулы связи координат точек картинной и предметной плоскостей, когда начало координат находится в главных точках схода I и I'.

Часто за начало координат аэроснимка принимают точку нулевых искажений с, главную точку о или точку надира n. Преобразуем полученные формулы, приняв за начало координат точки с, о, n.

Начало координат находится в точке нулевых искажений с и ее проекции С.

За ось на снимке принята линия неискаженных масштабов, за ось - главная вертикаль. На местности за ось принята линия параллельная линии неискаженных масштабов, за ось 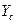- линия направления съемки. Точка нулевых искажений с также находится на главной вертикали uV, что и точка схода и на местности проекция точки нулевых искажений лежит на линии направления съемки, то есть на оси ординат, следовательно абсциссы точек не изменяются .

(44)

В соответствии с рис. 28

(45)

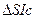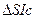В треугольнике угол при вершине I равен a, угол при вершине S равен , следовательно угол при вершине с равен , то есть треугольник равнобедренный и

, (35)

тогда

. (46)

Подставим значение из формулы (46) в выражение (44)

. (47)

На основании рис. 28 можно записать

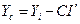(48)

В треугольнике угол при вершине I' равен a, угол при вершине С равен , следовательно треугольник также равнобедренный и

. (39)

С учетом равенств (39), (43) и (46) уравнение (48) примет вид

(49)

Начало координат находится в главной точке снимка о и ее проекции на местности точке О.

Так как ось ординат на снимке совпадает с главной вертикалью, а на местности с линией направления съемки, то абсциссы точек не изменятся, то есть .

В соответствии с рис.29

, (50)

где

, (34)

тогда

. (51)

Подставим полученное значение в формулу (42)

.

Приведя выражение в скобках к общему знаменателю получим

. (52)

На основании рис.29

(53)

где , тогда

. (54)

Подставим полученное значение в формулу (53)

. (55)

Начало координат в точке надира снимка n и ее проекции на местности точке N.

Как и в предыдущих случаях абсциссы точек не изменятся .

На основании рис.30

, (56)

где значение In найдем из пря­моугольного треуголь­ника

, (57)

тогда

. (58)

Подставим полученное значение в формулу (42).

. (59)

Значение ординаты 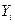как видно из рис.30 будет

(60)

Вместо 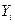и подставим в равенство (60) их значения из формул (38) и (43).

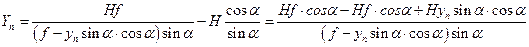
. (61)

В рассмотренных системах координат связь между координатами точек картинной и предметной плоскостей устанавливается через элементы внутреннего и внешнего ориентирования. Для горизонта­льного снимка точки надира, нулевых искажений и главная совпада­ют. В этом случае формулы связи координат получим, подставив в выражения (42), (43), (47), (49), (59), (61)

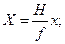(62) (63)