Искажение направлений под влиянием наклона снимка

За вершину направлений на аэроснимке выберем точку a (Рис.33).

Приняв за полюс точку нулевых искажений с, а за полярную ось - линию неискаженных масштабов h_ch_c будем иметь полярные координаты: угол j (Рис.33) и радиус - вектор r=ca. Про­ведем из точки а произвольное направление аi, составляющее с горизонталью h_ah_a угол g.

Найдем точку на местности соответствующую точке снимка a. Для этого продолжим линию ai до пересечения с линией основа­ния картины h_th_t, получим точку а_о. Центр проекции S соеди­ним с точкой i и из точки а_о проведем прямую параллельную Si.

Получим линию на местности, соответствующую линии аэроснимка ai на которой находится точка местности A. Для определения положения точки А проведем проектирующий луч Sа. который в пересечении с построенной прямой даст искомую точку. Через точку А проведем прямую перпендикулярно линии направления съемки VV. Угол между линиями h_ah_a и ААо обозначим g'. В плоскости действи­тельного горизонта G углу g' равен угол между линией дейс­твительного горизонта h_ih_i и линией Si, так как прямая h_ah_a параллельна линии действительного горизонта, а прямая Si параллельна линии ААо. В общем случав угол g' не равен углу g. Искажение направления вызванное наклоном аэроснимка Dg будет . (73)

Плоскость действительного горизонта G в которой лежат лучи SI и Si повернем вокруг линии действительного горизонта h_ih_i до совмещения с плоскостью снимка Р и так как треуго­льник 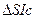равнобедренный точка S совпадает с точкой с (Рис.34). Горизонталь h_ah_a параллельна линии действительного горизонта h_ih_i, сле­довательно угол при точке i между ли­ниями h_ih_i и ia равен g, а угол при вершине i в треуго­льнике 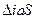равен -Dg. В этом же треугольнике угол при вершине a равен 180°-(j-g), а синус этого угла будет .

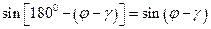Используя теорему си­нусов напишем

откуда

. (74)

Из прямоугольного треугольника 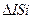имеем

, где ,

следовательно

. (75)

Подставим полученное значение Si в формулу (74)

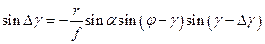
или

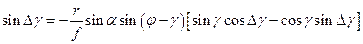. (76)

Поделим обе части уравнения (76) на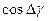

Перенесем члены содержащие влево

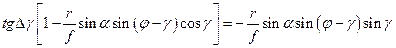. (77)

Решим равенство (77) относительно

. (77)

Как видно из выражения (78) величина искажения зависит от поляр­ных координат точки, из которой проведено направление r,j и от угла g. При r=0, Dg= 0, то есть наклон аэроснимка не искажает направлений выходящих из точки нулевых искажений c, следовательно, в этой точке углы на снимке равны соответственным углам на местнос­ти. Поэтому точка c и называется точкой нулевых искажений.

Для плановых аэроснимков формулу (78) можно упростить, отбросив в знаменателе второй член как малую величину, тогда

. (79)

Определим искажения направлений в главной точке о и точке надира n для планового аэроснимка. Для главной точки 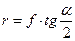и j=90°. Подставим эти вели­чины в формулу (79)

. (80)

Для точки надира 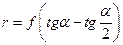и j=270°, тогда

. (81)

Таким образом в случае равнинной местности и при наличии наклона аэроснимка будут происходить искажения направлений. В точке c направления не искажаются. При a £ 1° для главной точки o и точки надира n ошибки направлений будут невелики, и ими можно пренебречь. При больших углах наклона аэроснимка за вершину направлений в фотограмметрических работах надо прини­мать точку нулевых искажений c.