СМО с очередью подразделяются на разные виды, в зависимости от того, как организована очередь—ограничена она или не ограничена. Ограничения могут касаться как длины очереди, так и времени ожидания (так называемые «СМО с нетерпеливыми заявками»). При анализе СМО должна учитываться также и «дисциплина обслуживания» — заявки могут обслуживаться либо в порядке поступления (раньше пришла, раньше обслуживается), либо в случайном порядке [2].
Рассмотрим математическую модель бизнес-процесса регистрации обращения, который, на мой взгляд, является проблемным. На рисунке 1.4 показан граф состояний системы массового обслуживания

Рисунок. 1.4 – Граф состояний СМО по обслуживанию членов профсоюза
Бизнес-процесс предполагает нахождение в очереди количества заявок, сопоставимого с вместимостью приемной профсоюза. На основе данных, полученных в ходе проведенного исследования, входящий поток заявок на обслуживание - простейший поток с средней интенсивностью λ = 7 заявок в час.
Интенсивность потока обслуживания положим равной µ. Длительность обслуживания - величина, которая зависит от скорости работы заместителя председателя и в среднем занимает 10 минут. Поток обслуживаний является простейшим пуассоновским потоком событий. Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания. Моделируемая СМО не может вместить более 15 заявок ввиду малых габаритов приемной профкома. Состояния СМО в таком случае можно представить следующим образом:
S0 - канал свободен;
S1 - канал занят, очереди нет;
S2 - канал занят, одна заявка в очереди;
…
S15 - канал занят, 14 заявок в очереди.
Таким образом, бизнес-процесс ожидания в очереди будет описываться следующей системой алгебраических уравнений:
1. Интенсивность поступления заявок в систему (заявок в час):
λ = 7;
2. Интенсивность обработки потока заявок (1/час):
µ=6
3. Приведенная интенсивность потока заявок:
ρ=λ/µ=1,16
4. Финальные вероятности системы:
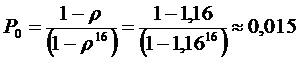
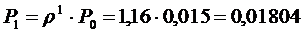
…
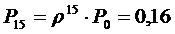
5. Вероятность отказа в обработке заявки
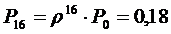
Зависимость финальных вероятностей системы от состояния системы показана на следующем графике (рисунок 1.5):
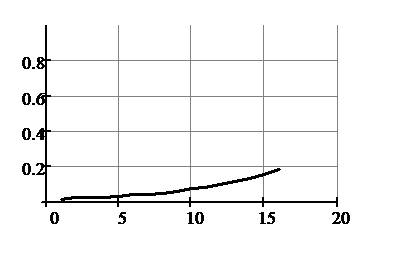
Рисунок 1.5 – График финальных вероятностей системы
6. Относительная пропускная способность системы:
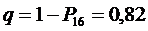
7. Абсолютная пропускная способность системы:
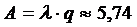
8. Среднее число заявок в системе:
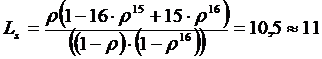
9. Среднее время пребывания заявки в СМО (час):
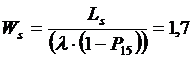
10. Среднее время пребывания заявки в ожидании оформления (час):
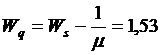
11. Средняя длина очереди:
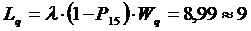
Основные параметры системы, которые важны с точки зрения работы профсоюза и решаемой в моей работе задачи, – это вероятность отказа и время пребывания заявок в очереди. Как видно из рисунка 1.5, увеличение роста заявок приводит к увеличению вероятности отказа, что крайне негативно влияет на работу профсоюза. Например, в пору окончания сезона, когда начинается увеличивается число обманов с выплатой заработной платы, интенсивность потока заявок может достигать 10-15 человек в час при неизменности остальных параметров. Тогда график финальных вероятностей будет выглядеть так, как показано на рисунке 1.6.
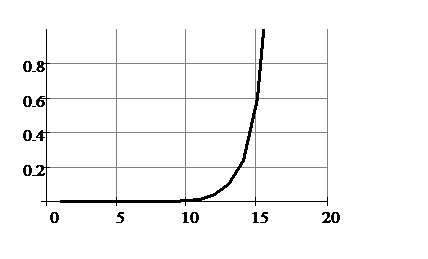
Рисунок 1.6 – График вероятностей состояния системы в моменты пиковой нагрузки
Следовательно, при увеличении потока заявок и неизменности остальных параметров системы, вероятность отказа стремится к 1, что говорит о невозможности функционирования профсоюза в таких условиях. Основной величиной, влияющей на вероятность отказа, в таком случае, является среднее время обслуживания заявки, то есть время работы заместителя председателя, которое тратится на работу с обращениями.