Метод координатного спуска [96-97]- простейший метод поиска экстремума функции.Он заключается в изменении каждый раз одной переменной,тогда как другие при этом остаются постоянными,пока не достигнут экстремум.Алгоритм состоит из следующих операций.Прежде всего,задаются начальные значения переменных  ,а также начальные приращения
,а также начальные приращения  и вычисляется значение функции в начальной точке
и вычисляется значение функции в начальной точке  .Затем в циклическом порядке изменяется каждая переменная(каждый раз только одна),на выбранные величины приравнений.В частности
.Затем в циклическом порядке изменяется каждая переменная(каждый раз только одна),на выбранные величины приравнений.В частности  изменяется на величину
изменяется на величину  ,так что
,так что  .Если это изменение не улучшает целевую функцию
.Если это изменение не улучшает целевую функцию  ,то
,то  изменяется на
изменяется на  и значение
и значение  проверяется как и ранее.Если
проверяется как и ранее.Если  не улучшает ни
не улучшает ни  ,ни
,ни  ,то
,то  оставляют без изменений и переходят к изменению величины
оставляют без изменений и переходят к изменению величины  .Этот алгоритм сходится медленно если имеет место взаимодействие между переменными,т.е если выражение для целевой функции ыходят члены,содержащие
.Этот алгоритм сходится медленно если имеет место взаимодействие между переменными,т.е если выражение для целевой функции ыходят члены,содержащие  .Алгоритм способен отыскать только локальный экстремум вблизи начальных значений аргументов.
.Алгоритм способен отыскать только локальный экстремум вблизи начальных значений аргументов.
Градиентный метод
Градиентный метод [96-98] реализует итерационную процедуру движения к максимуму на произвольно выбранной точки начального приближения в направлении наиболее сильного возрастания функции,определенном в окрестности текущего значения аргумента.Направление определяется вектором градиента  .Направление определяется вектором градиента.Новое приближение аргумента
.Направление определяется вектором градиента.Новое приближение аргумента  по значению
по значению  ,найденному на предыдущем шаге работы алгоритма наискорейшего спуска вычисляется по формуле
,найденному на предыдущем шаге работы алгоритма наискорейшего спуска вычисляется по формуле  , где
, где  - градиентный шаг.Значение градиента функции в данной точке оценивается с помощью разностной схемы.
- градиентный шаг.Значение градиента функции в данной точке оценивается с помощью разностной схемы.
При экспериментальной реализации в линейной системе возможно одновременно измерить отклики на приращения по различным координатам.Для этого по различным координатам приращения вводятся с различными частотами[97].Это позволяет с помощью синхронного детектора выделить отклики на приращения координат.
|
|
Вычисление всех компонент градиента возможно за один шаг в методе стохатической градиентной оптимизации[97].Для этого необходимо чтобы компоненты  пробного шага
пробного шага  были случайными числами со следующими характеристиками:
были случайными числами со следующими характеристиками:
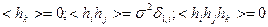 .Таким образом если приращение оптимизируемого критерия
.Таким образом если приращение оптимизируемого критерия  ,то произведение
,то произведение  позволяет “в среднем” вычислить значения всех компонентов градиента за один шаг.
позволяет “в среднем” вычислить значения всех компонентов градиента за один шаг.
Геометрическая интерпретация алгоритма наискорейшего спуска траектория  оригинальна линиям равного уровня минимизируемой функции.Поскольку шаг движения к экстремуму имеет конечную длину,по мере перемещения к точке
оригинальна линиям равного уровня минимизируемой функции.Поскольку шаг движения к экстремуму имеет конечную длину,по мере перемещения к точке  ортогональность нарушается.В точке
ортогональность нарушается.В точке  направление корректируется и снова становится ортогональным к линиям равного уровня.
направление корректируется и снова становится ортогональным к линиям равного уровня.
В работах [56,91] рассматривается алгоритм последовательного градиента спуска.В простейшем случае по известному грапдиенту функционала ошибки вычисляются новое приближение комплексной амплитуды:
 , где
, где  - длина шага градиентного метода, а
- длина шага градиентного метода, а  - градиент среднеквадратической ошибки отклонения распределения интенсивности получаемого после итерации и истинного распределения в выходной плоскости.Для ускорения процесса сходимости приближенного решения к точному,иногда предлагается использовать на последнем шаге алгоритма дополнительную оптимизацию параметров,например,длины шага.
- градиент среднеквадратической ошибки отклонения распределения интенсивности получаемого после итерации и истинного распределения в выходной плоскости.Для ускорения процесса сходимости приближенного решения к точному,иногда предлагается использовать на последнем шаге алгоритма дополнительную оптимизацию параметров,например,длины шага.
|
|
Преимущество градиентного метода - высокая скорость работы.Недостатками являются возможность отыскания лишь локального экстремума оптимизируемой функции,неустойчивость при наличии помех,зависимость от начальных условий.
 Отсюда, переход к следующему приближению по методу Ньютона осуществляется по формуле:
Отсюда, переход к следующему приближению по методу Ньютона осуществляется по формуле:
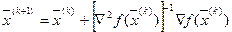 , где
, где  - матрица, обратная матрице вторых частных производных
- матрица, обратная матрице вторых частных производных  по
по 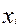 , взятая в точке
, взятая в точке  . Направление и величина шага точно определены. Если
. Направление и величина шага точно определены. Если  - квадратичная функция, то для достижения экстремума достаточно одного шага. В случае общей нелинейности, экстремума за один шаг достичь нельзя.
- квадратичная функция, то для достижения экстремума достаточно одного шага. В случае общей нелинейности, экстремума за один шаг достичь нельзя.
Методы локального поиска эффективны при отыскании экстремума функции, которая не имеет большого количества экстремумов или отыскание именно глобального экстремума не является обязательным. В случае, если целевая функция является многоэкстремальной и отыскание глобального экстремума обязательно, необходимы алгоритмы, позволяющие оптимизировать многоэкстремальные функции. Одним из таких алгоритмов является симплекс-метод.
Симплекс-метод
Симплекс-метод [98-99] является методом прямого поиска. Благодаря простоте и высокой эффективности при оптимизации сложных функций, этот метод получил широкое распространение [100]. Метод заключается в том, что движение к оптимальному значению аргументов функции осуществляется путем последовательных отражений некой фигуры, называемой симплексом. В m-мерном пространстве (целевая функция имеет m переменных) симплекс представляет собой фигуру с m+1 вершинами, не принадлежащую одновременно ни одному пространству меньшей размерности. Так, в одномерном случае симплекс является отрезком, в двумерном – треугольником, в трехмерном – тетраэдром. Чаще всего используются симплексы с равными расстояниями между вершинами. Измеряются значения целевой функции в вершинах симплекса. При поиске максимума движение происходит от вершины с наименьшим значением целевой функции к противоположной грани симплекса, который является зеркальным отражением предыдущего относительно грани, противоположной вершине с наименьшим значением целевой функции. Многократное отражение наихудших вершин приводит к шаговому движению центра симплекса к цели по некоторой ломаной линии (рис.1.16). За исключением начального момента, когда необходимо вычислить m+1 значение функции, на каждой итерации требуется всего одно ее вычисление.
|
|
Постоянный размер симплекса не обеспечивает одновременно и высокую скорость движения симплекса и точность отыскивания экстремума. Поэтому для быстрого и точного решения задачи требуется изменение размеров симплекса в процессе поиска. Этот метод предусматривает постепенное уменьшение

Рис.1.16. Характерное движение симплекса на плоскости двух переменных
расстояние между вершинами симплекса с сохранением одной вершины (последней найденной вершины или вершины с наилучшим значением оптимизируемой функции).
Симплекс-метод не уступает по эффективности градиентным методам, при этом существует возможность нахождения глобального экстремума оптимизируемой функции.
Кроме того, алгоритм не требует сложных вычислений, все операции формализованы, каждое измерение целевой функции позволяет двигаться к цели. Однако эффективность этого метода снижается при наличии помех. Для эффективной работы алгоритма необходимо, чтобы положение максимума целевой функции не менялось со временем и не зависело от предыстории, а целевая функция была стационарна во времени, что часто не выполняется в оптических системах, например, из-за гистерезиса адаптивного зеркала и изменения функций отклика адаптивного зеркала вследствие его нагрева или деполяризации.
Генетический алгоритм
Часто оптимизируемая функция обладает большим количеством экстремумов. Это обстоятельство значительно затрудняет применение классических методов оптимизации. В связи с этим встает задача построения таких методов оптимизации, которые были бы способны отыскивать решения практически при полном отсутствии предложении о характере исследуемой функции. Одними из таких методов являются так называемые эволюционные методы поиска и, в частности, генетические алгоритмы, моделирующие процессы природной эволюции.
Генетические алгоритмы предназначены для решения задач оптимизации, например, нахождение максимального значения функции. В основе генетического алгоритма лежит метод случайного поиска. Основным недостатком случайного поиска является то, что часто необходимо значительное время для решения задачи. Для того, чтобы избежать таких расходов времени, применяются биологические методы, открытые при изучении эволюции и происхождение видов. Как известно, в процессе эволюции выживают наиболее приспособленные особи. Это приводит к тому, что приспособленность популяции возрастает, позволяя ей лучше выживать в изменяющихся условиях.
Впервые численный алгоритм, основанный на имитации развития популяции, был предложен в 1975 году Джоном Холландом (Jhon Holland) [102]. Он получил название «репродуктивный план Холланда» и лег в основу вариантов генетических алгоритмов.
Представление объектов
Из биологии известно, что любой организм может быть своим фенотипом, который фактически определяет, чем является объект в реальном мире, и генотипом, который содержит всю информацию об объекте на уровне хромосомного набора [103]. При этом каждый ген, то есть элемент информации генотипа, имеет свое отражение в фенотипе. Таким образом, для решения задач нам необходимо представить каждый признак объекта в форме, подходящей для использования в генетическом алгоритме. В наиболее часто встречающейся разновидности генетического алгоритма для представления генотипа объекта применяются числовые массивы. В задаче нахождения глобального экстремума какой-либо функции, этот числовой массив соответствует набору аргументов этой функции. Значение этой функции - есть числовое представление фенотипа. Таким образом, каждая особь со своим генотипом и фенотипом представляет собой возможное решение задачи оптимизации[104].
Для того чтобы определить фенотип объекта (то есть значения признаков, описывающих объект) нам необходимо только знать значение генов, то есть генотип объекта. Его также называют особью. Таким образом, в реализации генетического адгоритма хромосома(упорядоченная последовательность генов) представляет собой массив чисел генов фиксированной длины.