Распределение Вагнера определяется, как пространственное Фурье-преобразование корреляционной функции плотности:
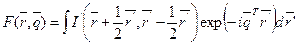(2.49)
Функция Вигнера была введена для описания распределения фазы в квантовой механике
[137]. Любой лазерный пучок может быть охарактеризован моментами второго порядка распределения Вигнера. Распределение Вигнера является наиболее полным описанием лазерных пучков в плоскости измерения.
Распределение интенсивности связано с распределением Вигнера следующим соотношением:
(2.50)
Где вектов q определяется угловыми переменными по двум перпендикулярным осям
Моменты второго порядка распределения Вигнера позволяют очень быстро и легко описать свойства пучка, распространяющегося через оптичскую систему.
Моменты распределения Вигнера определены как:
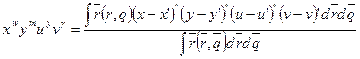(2.51)
Одномерное распределение Вигнера является функцикй одной пространственной координаты
x и одной угловой u. Распространение пучка через оптическую систему описывается формулой:
(2.52)
Как в двумерной случае распределение плотности мощности получается интегрированием по угловой переменной:
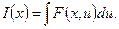(2.53)
Следовательно, учитывая распределение Вигнера F(x,u) задаваемое формусой (2.52),
Распределение интенсивности при прохождении пучком оптической системы с матрицей S, выглядит следующим образом:
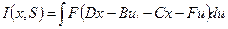(2.54)
Преобразование Фурье уравнения (2.54) приводит к выражению:
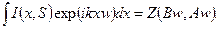(2.55)
где
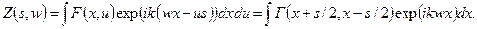(2.56)
Двумерное преобразование Фурье распределения Вигнера (Двумерное ПФВ). Из уравнения (2.55) видно, что преобразование Фурье распределения интенсивности можно рассматривать, как центральный слой двумерного ПФВ в плоскости пучка (рис.2.7). Следовательно, двумерное ПФВ можно получить, измеряя послойно распределение плотности мощности.
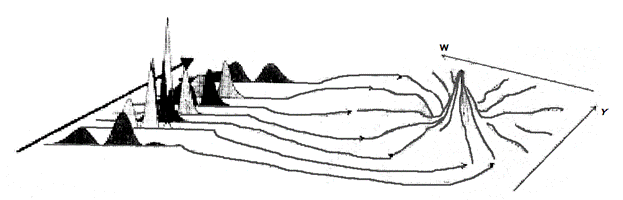
Рис. 2.7. Восстановление двумерного ПФВ с помощью измеренных распределений интенсивности. Преобразование Фурье каждого профиля интенсивности дает слой двумерного ПФВ.
Самая простая оптическая система для получения двумерного ПФВ – свободное распространение на расстояние z, S 
.При использовании уравнения (2.55) получается
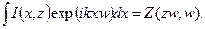(2.57)
Количество измерений и их положение, необходимые для осуществления оптимального моделирования двумерного ПФВ, очевидно, зависит непосредственно от самого двумерного ПФВ. Наилучший результат можно получить, если измерить распределение интенсивности в радиусе трех длин Релея от положения перетяжки [137], при этом расстояния до перетяжки (рис.2.8). Если перетяжки пучка недоступна, то её обычно создают искусственно с помощью линзы. Следовательно, требуемая процедура измерения подобна процедуре, описанной в стандарте ISO 11146, где подобный метод предложен для определения параметров пучка. На рис.2.8 изображена схема эксперимента для определения двумерного ПФВ.
Преимущество использования данного метода состоит в том, что все данные для восстановления всех проекций распределения Вигнера могут быть получены сразу посредством только одного сканирования каустики.