В международном стандарте ISO 11146 [130] определяются методы измерения и расчета таких параметров пучка, как диаметр пучка, угол расходимости и параметр качества пучка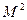 
. Предлагаемые методы неприменимы для расчета характеристик лазеров с неустойчивым резонатором, а так же пучков, прошедших через диафрагму [132]. Согласно стандарту, любой радиально симметричный пучок можно описать тремя параметрами:
· Положение перетяжки пучка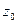 
;
· Диаметр перетяжки 
;
· Угол расходимости в дальней зоне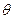 
;
С помощью этих параметров можно вычислить диаметр пучка на любом расстоянии от лазера:
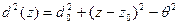(2.9)
Распространение пучка также можно описать с помощью параметра качества 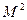, который вычисляется с помощью трех основных характеристик пучка. Соотношение между 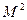, диаметром перетяжки 
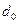и углом расходимости следующее :
, 
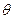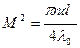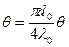(2.10)
где
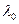- длина волны в вакууме;
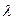- длина волны в среде с коэффициентом преломления
- коэффициент преломления
Это соотношение описывает распространение пучка в свободном пространстве с коэффициентом преломления и инвариантно на всем протяжении пучка. В случае эллиптического пучка (рис 2.2) описание сводится к семи параметрам:
· Положение перетяжки пучка 
, 
;
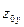· Диаметры перетяжки 
, 
;
· Углы расходимости в дальней зоне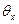 
, 
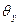
· Угол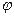 
между осью x пучка и осью лабораторной системы.
Аналогично радиально симметричному пучку, эллиптический пучок можно описать параметрами качества относительно осей x и y - 
, 
.
, 
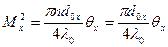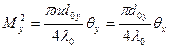(2.11)
Диаметр пучка определяется для радиально симметричного пучка, как
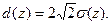(2.12)
а для эллиптического
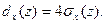
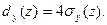(2.13)
Где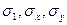 
- вторые моменты распределения интенсивности.
Первые моменты характеризуют центр тяжести пучка и определяются, как:
, 
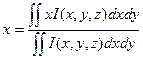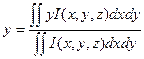(2.14)
Где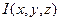 
- интенсивность пучка.
Вторые моменты характеризуют диаметр пучка и угол расходимости [130] и вычисляются с использованием следующих формул для полярной и декартовой системы координат соответственно:
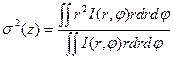
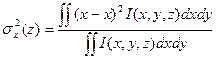(2.15)
Здесь r - расстояние до центра тяжести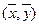 
, координаты которого дают первые моменты. Интегрирование ведется по всей плоскости xy.
Для определения диаметра пучка в положении z используется распределение интенсивности в плоскости xy. Согласно международному стандарту ISO 11146 [130], измерение интенсивности для каждого положения z должно проводиться не менее пяти раз. Исходя из результатов измерений интенсивности вычисляются первые
4) Островная модель генетического алгоритма [104]. Эта модификация также заимствована из биологии с следующей ситуации: имеется группа близкорасположенных островов, на которых живут популяции особей одного вида. Эти популяции развиваются независимо, и только изредка происходит обмен представителями между популяциями. Основная модель генетического алгоритма использует описанный принцип для поиска решения. Данная модель генетического алгоритма обладает следующими свойствами:
· Наличие нескольких популяции, как правило, одинакового фиксированного размера.
· Любые комбинации стратегий отбора и формирования следующего поколения в каждой популяции. Можно сделать так, что в разных популяциях будут использоваться разные комбинации стратегий.
· Ограничений на тип кроссовера и тип мутаций нет.
· Случайный обмен особями между «островами» после определенного шага схемы генетического алгоритма.
5) Алгоритм с периодическим перезапуском [109]. Данный алгоритм довольно быстро сходится из-за того, что в нем нет мутаций, используются популяций небольшого размера, и отбор особей в следующее поколение ведется и между родительскими особями и между потомками. Из-за этого после некоторого количества эпох алгоритм может сойтись к локальному экстремуму. После этого алгоритм перезапускается, причем лучшая особь копируется в новую популяцию, а оставшиеся особи подвергаются сильной мутации (мутирует примерно треть генов хромосомы) и поиск повторяется. Ещё одной специфической чертой является стратегия скрещивания: все особи разбиваются на пары, причем скрещиваются только те пары, в которых хромосомы особей существенно различны. При скрещивании используется так называемый – половинный однородный кроссовер – это разновидность кроссовера, в котором каждому потомку попадает ровно половина генов хромосомы от каждого родителя. Таким образом, модель обладает следующими свойствами:
· Фиксированный размер популяции.
· Перезапуск алгоритма после нахождения решения после определенного шага.
· Небольшая популяция.
· Особи для скрещивания разбиваются на пары и скрещиваются при условии существенных отличий.
· Отбор в следующее поколение проводится между родительскими особями и потомками.
· Используется половинный однородный кроссовер.
· Макромутация при перезапуске.
Какой из перечисленных алгоритмов наиболее эффективен, зависит от решаемой задачи и вида оптимизируемой функции.
Таким образом, генетические алгоритмы представляют мощный аппарат для решения задач оптимизации. Разработано большое количество различных модификаций и усовершенствований генетического алгоритма, которые повышают его эффективность и позволяют с той или иной степенью точности предсказать требуемое вычислительное время [106,110]. В последнее время генетический алгоритм нашёл широкое применение для решения различных прикладных задач лазерной физики [107-108,111-112].
Выводы:
Таким образом, подводя сравнение различных итерационных алгоритмов можно сделать следующие выводы:
1) алгоритм последовательного градиентного спуска для случая восстановления фазы по одному распределению интенсивности эквивалентен алгоритму минимизации ошибки, а в случае двух известных распределений интенсивности имеет сходство с алгоритмом Гершберга- Сакстона;
2) важным критерием при выборе того или иного метода является скорость его сходимости. В ходе исследований было установлено, что наиболее быстрой сходимостью из предложенных методов обладает INPUT-OUTPUT алгоритм.
3) вопрос получения однозначного решения для задачи восстановления фазы из распределений интенсивности так же представляет большой интерес. При решении двумерных задач данные методы позволяют получить однозначное распределение фазы.
4) алгоритмы глобального поиска имитирующие процессы эволюции в природе способны отыскать глобальный экстремум многоэкстремальной функции.