В данной главе рассматриваются известные в литературе методы рещения задач коррекции аберраций и формирования заданных распределений световых полей. Их можно классифицировать по двум признакам: во-первых, по выбору оптических элементов или оптических систем, осуществляющих коррекцию или формирование, а во-вторых, по реализации алгоритма восстановления фазы, которую выбранная оптическая система задает исходной световой волне. В соответствии с первым критерием можно выделить оптические системы, основание на голографических фильтрах, дифракционных элементах, рефрактивные оптические системы и, наконец, системы, основным элементов которых являются деформируемые зеркала. Выбор того или иного метода определяется поставленной задачей.
Во второй половине 20-го века лазеры начинают использовать для изготовления голограмм. Основное требование, предъявляемое в данном случае к изучению, состоит в возможно более равномерном распределении интенсивности по сечению пучка. Для формирования подобного профиля интенсивности предлагалось использовать диафрагмы и фильтры, с коэффициентов пропускания, экспоненциально возрастающим к периферии пучка [7-8] или мягкие диафрагмы. Они позволяют сгладить пространственное распределение интенсивности пучка, увеличить стабильность мощных лазерных пучков, оптимизировать заполнение активной среды и улучшить эффективность преобразования частоты излучения [9]. В работе [10] изучается возможность создания мягких диафрагм на основе кюветы с красителем для аподизации пучков излучения мощных лазеров. Для компенсации фазовых искажений в лазерном пучке, прошедшим мягкую диафрагму, предложена конструкция кюветы с вкладышем в виде мениска. Демонстрируется технология Формирования мягких апертур при лазерной обработке пластин прозрачного диэлектрика. Полученные результаты обосновывают возможность создания на основе кюветы с просветляющим красителем высокоапертурного оптического элемента – развязки аподизатора для применения в усилительных каскадах мощных неодимовых, йодных и эксимерных лазеров. Но, как оказалось, применение таких диафрагм сопряжено с большими потерями энергии [11]. Так, например, при использовании диафрагм эффективно исользовались только 5% исходного излучеия. Применение фильтров позволяло сохранить до 40% излучения [12]. Для повышения эффективности формирования были предложены многоапертурные интегрирующие системы или, так называемые, гомогенизаторы [11-13]. Их действие основано на принципе наложения и заключается в следующем: с помощью специального массива оптических элементов, например, микролинз (рис.1.1), плоских (рис.1.2) или выпуклых зеркал, исходных пучок ращепляется на несколько частей, которые затем отклоняются так, чтобы в некоторой плоскости сформировать заданное распределение интенсивности. За счет подобного наложения пучков достигается хорошая точность формирования равномерного распределения интенсивности. Такие системы успешно применяются для формирования многомодового излучения, так как из-за слабой степени пространственной когерентности излучения эффекты интерференции существенно подавляются. Однако, данная методика не является эффективной при необходимости формирования в выходной плоскости пучка не только с заданным профилем интенсивности, но и с определенной формой волнового фронта.


Рис. 1.1. Схема интегрирующей системы Рис. 1.2. Интегратор, использующий плоские зеркала
Помимо вышеизложенных способов формирования лазерного излучения, перспективным является использование элементов, изменяющих исключительно фазу световго излучения, а не его амплитуду. Как известно, комплексное поле  световой волны можно представить через амплитуду волны
световой волны можно представить через амплитуду волны  и фазу
и фазу  следующим образом:
следующим образом:
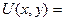
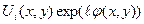
Распространение этой волны, скажем, от входной до выходной плоскости системы, можно рассчитать, использую интеграл Френеля-Кирхгофа:
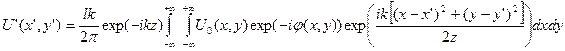 , (1.2)
, (1.2)
где (x,y), (x’,y’) – декартовы координаты во входной и в выходной плоскостях соответственно,  ,
,  – амплитуда световой волны во входной и в выходной плоскости соответственно, k – волновой вектор, z – расстояние между плоскостями. Из этого уравнения следует, что формирование требуемого светового поля возможно при задании соответствующего фазового профиля у исходной волны.
– амплитуда световой волны во входной и в выходной плоскости соответственно, k – волновой вектор, z – расстояние между плоскостями. Из этого уравнения следует, что формирование требуемого светового поля возможно при задании соответствующего фазового профиля у исходной волны.
Этот принцип лежит в основе большинства разработанных на данный момент методов. Выбор оптической системы, воздействующей на фазу световой волны, определяет отличие одного метода от другого.

Рис.1.3. Рефрактивная система, состоящая из двух асферических поверхностей
Возможности формирования лазерного излучения с помощью оптических элементов, основанных на эффекте преломления (Refractive Beam Shapers) активно исследовались несколькими научными группами. В работе приводится оптическая системы, состоящая и двух асферических поверхностей (рис.1.3), предназначенных для трансформирования пучка с гауссовыми профилем интенсивности в плоскую волну с равномерным распределением интенсивности. При расчете профилей данных поверхностей, авторы опирались на аппарат геометрической оптики. Рефрактивная система, приведенная в работе представляла собой одиночный элемент, состоящий из двух асферрческих поверхностей (рис.1.4.), и предназначалась для формирования Бесселева пучка нулевого порядка из пучка со следующими кольцевым распределением интенсивности:

Где  - параметры, определяющие используемые лазером. В основу расчета радиуса кривизны и асферичности поверхностей рефрактивных элементов положены следующие ограничения: энергия пучка при проходе через систему должна сохраняться, оптические длины для всех лучей должны быть одинаковыми. Помимо этого должно выполняться улсовие параллельности выходного пучка исходному. Подобные оптические элементы могут успешно применяться для решения довольно простых задач для формирования, однако, использование их в более сложных случаях ограничено трудоемкостью расчета и изготовления таких асферических поверхностей.
- параметры, определяющие используемые лазером. В основу расчета радиуса кривизны и асферичности поверхностей рефрактивных элементов положены следующие ограничения: энергия пучка при проходе через систему должна сохраняться, оптические длины для всех лучей должны быть одинаковыми. Помимо этого должно выполняться улсовие параллельности выходного пучка исходному. Подобные оптические элементы могут успешно применяться для решения довольно простых задач для формирования, однако, использование их в более сложных случаях ограничено трудоемкостью расчета и изготовления таких асферических поверхностей.
Одним из широко используемых способов управления и коррекции лазерного излучения в последнее время является применение жидкокристаллических управляемых транспарантов. С их помощью возможно создание управляемых линз, призм, дифракционных решеток. Принципиальная конструкция жидкокристаллического транспаранта следующая. В зазоре между двумя кварцевыми пластинами заливается нематический жидкий кристалл. На внутренних поверхностях пластин известны прозрачные электроды, представляющие собой сетку из большого числа элементов, и ориентирующие покрытия, придающие жидкому кристаллу свойства, эквивалентные свойствам монокристалла с оптической осью, ориентированной в заданном направлении. Электрическое поле изменяет показатель преломления кристалла. Функции отклика такого кристалла, т.е. вносимое в волной фронт воздействие при подаче напряжения на один электрод, представляют собой ступеньки, локализованные в местах расположения электродов.
Еще одной возможностью применения жидких кристаллов для управления излучением является использование оптически управляемого жидкокристаллического модулятора света. Принцип его действия основан на следующем. Выбитые падающим излучением фотоносители дрейфуют во внешнем электрическом поле. Они создают пространственный заряд, который определяет поле в объеме электрооптического материала, что, в свою очередь, определяет его оптические свойства. Усовершенствование электрооптических модуляторов было направлено, в основном, на увеличение их чуствительности к управляющему излучение, уменьшение времени отклика и увеличение разрешение. Эти модуляторы широко применяются в работающих в реальном времени системах обработки изображения, система детектирования и визуализации. В работе [22] рассмотрено применение жидкокристаллического модулятора при интерферометрическом измерении вибраций стеклянной пластины в реальном времени. Возможно применение этих корректоров для обращения волнового фронта, коррекции аберраций [21].
Достоинствами жидкокристаллического транспаранта являются возможность модулировать волновой фронт в достаточно широких пределах (несколько десятков микрон), локальность функции отклика, высокая прозрачность в широком спектральном диапазоне. Жидкие кристаллы не требуют громоздких блоков управления, высокого приложения. Однако их существенным недостатком является неоднозначность функции отклика при включении и выключении, а также требование низких мощностей пучка [23].
Среди основных направлений, разрабатываемых в дифракционной оптике для решения задач фокусировки а заданную область, можно выделать компьютерное моделирование голограмм (Computer-Generated Holograms) [24-29] и расчет дифракционных фазовых элементов (Diffractive Phase Elements) [30-37]. В работе [28] излагается методика формирования коллимированного пучка с равномерным распределением интенсивности из пучка с гауссовым профилем с помощью голографических фильтров (рис.1.5). В данной схеме используется два фильтра, первый из которых (H1) трансформирует исходный пучок в пучок с требуемым профилем интенсивности в ближнем поле, а второй (H2) корректирует фазу выходного пучка. Помимо этого в статье проводится сравнение нескольких методик расчета фильтров. С помощью таких фильтров достигается высокая точность формирования заданных профилей интенсивности.

Рис.1.5. Формирование пучка с помощью голографических пластин
Методы голографии можно использовать и для стационарной коррекции аберраций оптических систем [38]. Для этого сначала на фотографическую пластину записывается интерферограмма эталонной и прошедшей через оптическую систему с аберрациями волн. При восстановлении эталонной волной выходящее поле будет иметь искажения волнового фронта, обращенной по отношению к исходной волне, использовавшейся для записи. При ее прохождении через оптическую систему в обратном направлении фазовые искажения, в линейном приближении, взаимно скомпенсируются.
Однако, следует отметить ряд недостатков голографических оптических элементов. Во-первых, их использование налагает серьезные требования к технологии голографической записи. Во-вторых, они очень чувствительны даже к малым разъюстировкам оптической схемы. В-третьих, эффективность коррекции и формировании определяется дифракционной эффективностью голограммы, которая у обычных абсорбционных голограмм является крайне низкой (≈1%). Несмотря на то, что впоследствии были разработаны оптические элементы, обеспечивающие дифракционную эффективность порядка 45% (так называемые Computer-Originated Holographic Optical Elemt – COHOE [30]), применение голографических фильтров возможно только для ограниченного круга задач и не подходит для мощных лазерных систем.
Новые возможности по сравнению с описанной техникой применения голограмм дает использование киноформов [39], Киноформ – это чисто фазовый объект, его дифракционная интенсивность значительно выше, чем у амплитудной голограммы. Его функция пропускания может быть рассчитана из анализа оптической схемы прибора или обращением измеренного волнового фронта [39]. Далее необходимый рельеф формируется либо на фотопластинке, а затем переводится в вариации толщины отбеливанием фотоматериала, либо на поверхности прозрачной платины выжиганием. Погрешности этого метода связаны с дискретной природой представления информации в ЭВМ и ограниченными возможностями устройств формирования рельефа на пластине. Основные недостатки таких элементов связаны, в основном, с дифракцией на растре, рассеянием света на фотоэмульсии, стационарностью получаемой голограммы, т.е невозможностью динамически корректировать аберрации. От последнего недостатка свободны голограммы на фоторефрактивных кристаллах и полимерах. Время отклика фоторефрактивных кристаллов около 1 мс, разрешение более 100 лип/мм [39]. Основной их недостаток – сложность в производстве, что выражается в большой стоимости. В полимерах оптические свойства изменяются из-за перехода из транс- в цис-изомерное состояние. Время релаксации зависит от температуры, и, вместо стационарной голограммы при комнатной температуре, при термостатировании с температурой 60-70 С получается голограмма, позволяющая корректировать аберрации с частотой до 10Гц.
Однако существует недостатки, общие для всех голограмм. Это, например, низкая дифракционная эффективность преобразования, возможность перекрытия порядков при сильных аберрациях высоких порядков и.т.п.
Дифракционные оптические элементы [31-37] имеют ряд преимуществ по сравнению с рефрактивными элементами и голограммами. Среди них можно отметить компактность конструкции, высокую дифракционную эффективность (>95%) и невысокую стоимость производства. В статье [37] представлены результаты формирования пучков с бесселевым и равномерным профилями интенсивностей из гауссового пучка. Схема использования дифракционных фазовых элементов приведена на рисунке 1.6.

Рис. 1.6. Схема формирующей системы с использованием дифракционных элементов.
Для управления и амплитудой и фазой излучения необходимо два фильтра (на рисунке DPE1 и DPE2). Они представляют собой фазовые элементы, комплексная функция пропускания которых записывается в виде  . Поле непосредственно после первого дифракционного элемента выглядит следующим образом:
. Поле непосредственно после первого дифракционного элемента выглядит следующим образом:

 (1.3)
(1.3)
а после второго:
 (1.4)
(1.4)
где –  ,
, 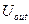 (x’, y’) поля во входной и выходной плоскостях, U’ (x’, y’) – поле в выходной плоскости, до прохождения через дифракционный фильтр, связанное с полем U (x, y) заданным оператором преобразования G: U’ (x’, y’)= G{U’ (x’, y’)}.
(x’, y’) поля во входной и выходной плоскостях, U’ (x’, y’) – поле в выходной плоскости, до прохождения через дифракционный фильтр, связанное с полем U (x, y) заданным оператором преобразования G: U’ (x’, y’)= G{U’ (x’, y’)}.
Например, в схеме рис.1.6 G – дифракционный интеграл распространения на расстояние z, определенный в формуле (1.2). каждый дифракционный элемент представлял собой набор 256 колец с заданной внутри каждого кольца постоянной фазой.
К отдельному классу дифракционных оптических элементов можно отнести, так называемые, дифракционные диффузоры. Фазовая функция такого диффузора рассчитывается с помощью следующего алгоритма [11]:
1) заданное в выходной плоскости распределение интенсивности домножается на случайную функцию (спекл-структуру),
2)вычисляется обратное преобразование Фурье от поля, интенсивность которого задана на первом шаге,
3)из рассчитанной во входной плоскости комплексной амплитуды определяется фазовая функция диффузора.
На рис.1.7 (а) представлен профиль, поверхности диффузора, позволяющего


(а) (б)
Рис.1.7 Формирование кольцевого распределения интенсивности:
а) фазовый профиль диффузора, б)полученное распределение интенсивности
сформировать кольцевое распределение интенсивности в дальнем поле, а на рис.1.7 (б) полученное распределение интенсивности. Подобные диффузоры успешно применяются при необходимости формирования сложных распределений интенсивности, логотипов и даже картин.
В последнее время разрабатываются диффузоры с улучшенными возможностями контроля распространения излучения [40]. Такой диффузор представляет собой микролинзовый растр (рис 1.8), Каждая микролинза растра характеризуется собственным радиусом кривизны, параметром асферичности и конической константой и рассчитывается в индивидуальном порядке. Для предотвращения дифракционных артефактов, расположение линз в растре задается в соответствии с вероятностной функцией Рэлея [41]. Подобный синтез детерминистического [42] и рандомизированного [11] подхода при создании диффузоров обеспечивает высокое качество формирования заданных профилей интенсивности (рис.1.9).




Рис.1.8.Микролинзовый Рис.1.9.Формирование заданных профилей
растр диффузора интенсивности с помощью диффузора
При решении задач коррекции аббераций или фокусировки мощного лазерного излучения качество формирования методами дифракционной оптики падает в связи с тепловыми искажениями, наводящимися лазерным излучением. В таких случаях более предпочтительным является применение ОВФ-зеркала или отражающей оптики. Методика ОВФ заключается во введении узла, который с помощью тех или иных малоинерционных физических процессов осуществляет операцию обращения волнового фронта [43]. При этом функция корректора, анализатора поля и системы управления объединены в одном устройстве. В результате ОВФ падающей волне придается прямо противоположное направление распространения и, с точностью до постоянного фазового множителя, комплексно сопряженное распределение амплитуды. Это означает, что у исходной и обращенной волн совпадают эквифазные поверхности и форма распределения интенсивности по сечению.
В качестве узла, реализующего операцию обращения волнового фронта, часто используется ОВФ-зеркало – нелинейный элемент, расположенный вместо глухого зеркала резонатора, в котором реализуется вынужденное бриллюоновское рассеяние. Недостатком обращения волнового фронта с помощью этого эффекта является наличие высокого порога по интенсивности, необходимость использования токсических веществ в качестве нелинейной среды [44]. Четырехволновое смещение мало эффективно, сложно реализовать из-за трудностей в юстировке, поэтому в работе [45] предлагается схема твердотельного АИГ лазера с самонакачиваемым векторным обращением. Было продемонстрировано исправление искусственно вводимых аббераций и возможность режима одномодовой генерации с помощью внутренних диафрагм.
Популярность ОВФ связана с тем, что эквифазные поверхности таких волн оказываются совпадающими не только вблизи узла, осуществляющего данную операцию, но и на любом удалении от него, даже когда среда, в которой они распространяются, является оптически неоднородной. Это позволяет компенсировать фазовые искажения в лазерных средах. Скорость выделении энергии оказывается настолько высокой, что ОВФ-зеркала обычно способны работать эффективно лишь короткое время. Также применение ОВФ-зеркал ограничивается его погрешностями функционирования, неравномерностью распределения усиления по сечению активного элемента (амплитудные абберации, приводящие в конечно итоге и к фазовым, с помощью методики ОВФ не компенсируются), наличием апертурных диафрагм [46].
При использовании зеркал достигается высокая эффективность трансформации излучения (в отличие от голографических фильтров), а также сохраняются когерентные свойства исходного излучения. Поэтому в ряде исследовательских лабораторий для формирования заданного профиля интенсивности пучка использовалось зеркало асферической формы. В работе [47] рассмотрен резонатор, одно из зеркал которого представляло из себя выпуклое сферическое зеркало с лункой в центре. Такая конструкция позволила значительно улучшить селективность резонатора. Такое асферическое зеркало также может быть использовано для компенсации различных искажений, вызванных термодеформацией активной среды [48].
В работе[49] задача формирования заданного профиля пучка решается путем пространственно неоднородного вывода энергии лазера, генерирующего основную моду. Однако излучение выводится не через неоднородное зеркало, а за счет отражения света от пластины с неоднородным покрытием, которая устанавливается внутрь резонатора под углом Брюстера к оптической оси. Светоделительная пластинка в этом эксперименте представляет собой прозрачную пластину с нанесенным вблизи оси пучка отражающим слоем диэлектрика. Эксперименты проводились с He-Ne лазером. Произведен расчет зависимости полных потерь отдельной моды от фазового сдвига, вносимого отражающим слоем. Показано, что как только потери основной моды, которые растут быстрее, сравниваются с потерями  моды, происходит значительное уменьшениевыходной мощности и качества пучка. Численные расчеты показали хорошее соответствие с экспериментом.
моды, происходит значительное уменьшениевыходной мощности и качества пучка. Численные расчеты показали хорошее соответствие с экспериментом.
Асферические зеркала успешно применяются в качестве внутризонаторных элементов для генерации заданных распределений интенсивности на выходе лазера. Эта идея была предложена еще в конце 70-х [49] однако широкое применение получила только с развитием техники алмазного точения, позволившей изготавливать такие зеркала с субмикронной степенью точности. В группе профессора Беланжера предложена и запатентована [50] методика расчета необходимых профилем поверхности, применяемых в качестве глухих зеркал устойчивых резонаторов  лазеров для формирования супергауссового распределения интенсивности низшей поперечной моды лазерного резонатора [51]. В результате проведенных экспериментов было зарегистрировано увеличение мощности низшей поперечной моды.
лазеров для формирования супергауссового распределения интенсивности низшей поперечной моды лазерного резонатора [51]. В результате проведенных экспериментов было зарегистрировано увеличение мощности низшей поперечной моды.
Другими исследовательскими группами также изучалась возможность формирования заданных профилей интенсивности с помощью асферических зеркал [52-55]. В работах [54-55] рассматривалась задача формирования пучка посредством зеркала с неаксиально-симметричным профилем поверхности. На рис.1.10 показана схема экспериментальной установки. Профиль поверхности зеркала рассчитывался в соответствии с методом стационарной фазы, более подробное рассмотрение которого, будет представлено в следующем параграфе. Распределение интенсивности, полученное с помощью данного зеркала, и профиль поверхности зеркала представлены на рис.1.11 и 1.12 соответственно. Из рисунка 1.11 видно, что распределение интенсивности с высокой точностью соответствует прямоугольному профилю, но к периферии пучка появляются острые скачки интенсивности. Это связано с технологическими погрешностями при изготовлении подобных зеркал. Максимальное отклонение профиля изготовленного зеркала от рассчитанного профиля составляло 10 нм для видимого диапазона света. Следовательно, при использовании подобных зеркал необходимо уделять внимание точности изготовления.

Рис.1.10.Схема экспериментальной установки, использующая зеркало с заданным профилем поверхности
Одним из широко используемых в последнее время пассивных способов формирования профиля интенсивности выходного излучения лазера является использование зеркал с промолулированным коэффициентом отражения (ЗПКО) [56]. Подбирая соответствующим образом профиль отражения таких зеркал, возможно сформировать, в ближнем поле основную поперечную моду резонатора, имеющую, например, супергауссовое распределение интенсивности [57]. Такое зеркало помещается вместо выходного зеркала резонатора. Для формирования супергауссового распределения интенсивности коэффициент отражения задается формулой:  , где
, где  - максимальный коэффициент отражения по интенсивности, r – радиус в полярных координатах, w - ширина пучка на зеркале, n - порядок супергаусса. Было показано, что использование ЗПКО в неустойчивых резонаторах импульсных твердотельных лазеров приводит к увеличению мощности генерации в основной поперечной моде в 1,6 раз, при этом одновременно улучшается качество пучка. Однако, т.к. ЗПКО вносят существенные дополнительные потери в резонатор лазера, то применение таких зеркал возможно лишь в лазерах с большим повышением над порогом генерации, то есть, как правило, имеющих неустойчивую конфигурацию резонатора [57].
- максимальный коэффициент отражения по интенсивности, r – радиус в полярных координатах, w - ширина пучка на зеркале, n - порядок супергаусса. Было показано, что использование ЗПКО в неустойчивых резонаторах импульсных твердотельных лазеров приводит к увеличению мощности генерации в основной поперечной моде в 1,6 раз, при этом одновременно улучшается качество пучка. Однако, т.к. ЗПКО вносят существенные дополнительные потери в резонатор лазера, то применение таких зеркал возможно лишь в лазерах с большим повышением над порогом генерации, то есть, как правило, имеющих неустойчивую конфигурацию резонатора [57].
В работе [58] было предложено использовать зеркала с коэффициентом отражения, модулированным за счет термооптического эффекта. Нагревание проводилось током, протекающим по боковой поверхности зеркала. Предложена теоретическая модель и продемонстрирована возможность применения таких зеркал.
Приведенные выше методы осуществляют формирование заданных распределений интенсивности, но не позволяют управлять световым пучком динамически. Для некоторых лазерных технологических установок это является существенной проблемой, так как эффективная работа подобных систем возможна лишь при стабильности параметров лазерного излучения. По ряду причин такое требование не всегда выполняется, например, из-за присущих лазерному пучку флуктуацией распределения интенсивности, рыскания пучка или из-за возможной


Рис.1.11.Распределение интенсивности в дальнем поле Рис.1.12.Профиль поверхности зеркала
Большой мощности светового пучка, приводящей к тепловым деформациям элементов лазера и формирующей оптики и к изменению их оптических характеристик. Иногда же сами условия технологического процесса требует изменения параметров светового пучка по заданной программе, то есть, необходим постоянный контроль и диагностика выходного лазерного излучения. Решением подобной проблемы является использование управляемых деформируемых зеркал, которые способны изменять свой профиль поверхности во времени.
Это свойство позволяет использовать деформируемые зеркала в составе систем с обратной связью для динамического управления лазерным излучением. В работе [55] для фокусировки пучка с гауссовым распределением в пучок с прямоугольным распределением интенсивности использовалось деформируемое зеркало с 9 управляющими электронами. В других научных группах [59-64] исследовались возможности управления лазерным излучением при помощи полупассивных биморфных гибких корректоров. Поэтому более универсальным и перспективным для технологических применений является использование гибких зеркал, профиль поверхности которых можно изменять в соответствии с требованиями эксперимента [65].
Одним из основных требований к адаптивным зеркалам является возможность компенсации максимального числа аббераций минимальным числом управляющих приводов. Поэтому главной характеристикой любого гибкого зеркала является функция отклика его приводов, под которой обычно понимается деформация поверхности корректора при подаче единичного управляющего напряжения на данный электрод.
Зеркала, деформация поверхности которых происходит в локальной области вблизи данного привода, называются корректорами с локальной функцией отклика [66]. К ним относятся сегментированные [66], мембранные [68], а также монолитные пьезозеркало [69]. Их достоинство состоит в основном в простоте расчета функций отклика и необходимого управляющего напряжения для аппроксимации требуемой поверхности. Недостатком является резкий скачок поверхности на границе сегментов, что приводит к ухудшению качества пучка. Поэтому предпочтительным является использование модальных корректоров, т.е. корректоров, вся поверхность которого деформируется при подаче управляющего напряжения на любой электрод.
Во многих работах показана возможность, использования такого корректора модального для управления выходным излучением лазера. В одной из первых работ [[70], посвященных проблеме внутрирезонаторного управления излучением с помощью гибких управляемых зеркал, рассмотрен  лазер с неустойчивым резонатором. Одно из зеркал этого лазера было заменено 19-ти элементным корректором, что позволило в 11 раз увеличить пиковое значение интенсивности в дальней зоне.
лазер с неустойчивым резонатором. Одно из зеркал этого лазера было заменено 19-ти элементным корректором, что позволило в 11 раз увеличить пиковое значение интенсивности в дальней зоне.
В работе [71] предложено в качестве глухого зеркала использовать механически нагруженную пластину с рассчитанной, переменной по радиусу толщиной. Величина подаваемой нагрузки определяется величиной термодеформаций активной среды. В аналогичной экспериментальной работе [72] была продемонстрирована эффективность применения зеркала постоянной толщины, что ограничивало спектр воспроизводимых аббераций только дефокусом и не влияло на селективность резонатора. В работе [73] в качестве глухого зеркала неустойчивого резонатора также использовался адаптивный корректор, воспроизводящий только дефокус для компенсации изменения параметров тепловой линзы, а для изменения профиля пучка применено зеркало с профилированным коэффициентом отражения. Было продемонстрировано сохранение качества пучка и его выходной мощности при изменении частоты повторения импульсов в 10 раз. В этом случае использовался корректор на основе биморфного пьезоэлемента, который состоит из двух соединенных между собой пьезокерамических пластин, поляризованных перпендикулярно широкой грани навстречу друг другу [73]. При подаче управляющего напряжения на электроды, нанесенные на пьезокерамику, под действием обратного пьезоэффекта, происходит расширение одной из пластин и сжатие другой, то есть возникает изгибающий момент, дефорирующий поверхность зеркала. В 1979 г. В работе С.Кокоровски было выведено уравнение деформации биморфного зеркала и решено для случая прямоугольной пластины [74]. Экспериментальный образец биморфного зеркала описывается в работе [75]. Однако изготовить (полировать, наносить покрытия, управляющие электроды) биморфные зеркала оказалось достаточно сложно. Более того, в задачах лазерной технологии адаптивные зеркала должны иметь систему охлаждения, которую невозможно сделать в тонкой ньезокерамической пластине. Поэтому в [76] было предложено использовать полупассивные биморфные корректоры (рис.1.13). Такое зеркало состоит из двух склеенных между собой, пластин: относительно толстой стеклянной или металлической подложки и тонкого пьезокерамического диска с электродами. Принцип работы такого корректора аналогичен биморфному зеркалу, однако чувствительность его ниже. В толще подложки могут быть сделаны каналы для охлаждения.

Рис.1.13.Полупассивный гибкий биморфный корректор
Экспериментальный образец круглого полупассивного биморфного зеркала описан в работе [77]. Он состоит из круглой стеклянной подложки и пьезодиска с одним общим электродом и 12-ю управляющими электродами в форме частей сектора. При толщине зеркала в 1,5 мм и диаметре 5 см его чувствительность составляла 1мкм на 100В. Характер деформации поверхности таких корректоров является модальным. Используя небольшое число управляющих электродов можно воспроизвести низшие абберации волнового фронта. Увеличивая число электродов и варьируя их положение, можно попытаться воспроизвести большое число аббераций.