В настоящей главе анализируется возможность использования адаптивной оптической системы на основе биморфных зеркал для улучшения качества фокусировки лазерного излучения [113-118]. Приводятся примеры использования адаптивной системы для управления фокусировкой лазерного излучения диодного и твердотельного YAG:Nd 
лазера [115-117]. В начале главы вводится понятие параметра качества пучка (
-фактора) [118-129], как параметра, с помощью которого можно правильно оценивать степень сфокусированного пучка по сравнению с гауссовым.
§ 2.1 Определение «степени фокусировки» пучка через понятие его качества ( -фактора)
При использовании лазерных установок в различных технологиях, например при термической обработке и резке металла, оптимальным является использование 
моды, которая соответствует гауссову пучку. Однако гауссов профиль распределения интенсивности лазерного излучения не означает, что пучок действительно является одномодовым [128], который не содержит моды, а получен суперпозицией мод более высокого порядка. Поэтому прежде, чем управлять фокусировкой излучения, встал вопрос о корректном «измерении» степени фокусировки пучка.
ВЫБЕРИ КАКОЙ БОЛЬШЕ НРАВИТСЯ
Рис 2.1. Распределение интенсивности (слева) и поперечное сечения пучка (справа).
Для сравнения степени фокусировки реального пучка с идеальным гауссовым удобно использовать так называемый параметр качества .
Этот параметр ввели специалисты по лазерной физике в конце 80-х годов.
Параметр должен был стать универсальным и характеризовать расходимость пучка в самых различных ситуациях [130-131]. представляет собой отношение диаметров произвольного и гауссова пучков в фокальной плоскости линзы. При этом полагается, что пучки имеют одинаковые диаметры перетяжки в ближней зоне 
.
Диаметр гауссова пучка в фокальной плоскости линзы 
можно рассчитать по следующей формуле [130]:
, (2.1)
Где 
- длина волны излучения, 
-фокусное расстояние линзы, 
- диаметр перетяжки пучка (наименьшее значение диаметра пучка на всем его протяжении).
При фокусировке произвольного лазерного излучения формула (2.1) принимает вид:
(2.2)
Таким образом, диаметр фокального пятна произвольного лазерного пучка в раз больше диаметра сфокусированного гауссова пучка. всегда больше единицы, причем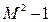 
только для идеального гауссова пучка.
К настоящему времени разработано большое количество методов для определения основных параметров лазерного излучения, от которых зависит - фактор [130-136]. К числу таких параметров относят диаметр пучка 
и угловую расходимость излучения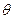 
[130].
Диаметр гауссова пучка при распространении может быть вычислен в соответствии со следующей формулой [130]:
(2.3)
Где 
- длина Релея, 
- диаметр пучка в плоскости перетяжки,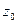 
- положение перетяжки относительно выходного зеркала лазера [130]. Длина Релея рассчитывается согласно следующей формуле:
(2.4)
Таким образом, распространение гауссова пучка полностью описывается размером его перетяжки и её положением . Для общего случая пучка с произвольным распределением интенсивности (рис 2.2) верна следующая формула:
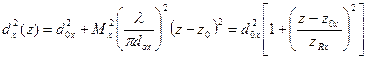(2.5)
(2.6)
Где 
, 
- диаметры пучка относительно главных осей пучка 
, 
и 
- параметр качества пучка относительно осей .
Рис 2.2. Сечение произвольного лазерного пучка: , - диаметры пучка,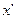 
и 
- лабораторная система координат, 
и 
- система координат, совпадающая с осями пучка,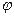 
- угол между лабораторной системой координат и главной осью пучка.
Другими словами, диаметр пятна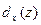 
и 
для произвольного пучка можно определить через размеры перетяжки 
и 
и её положение 
и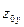 
, также, как через 
и 
определялся диаметр гауссова пучка. Кроме того, распространение пучка зависит от параметра качества пучка и . Для произвольного пучка 
- фактор вычисляется следующим образом:
, 
, (2.7)
Где 
, 
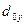- диаметр перетяжки, 
, 
- диаметр пучка в фокальной плоскости линзы f.
Исходя из уравнений (2.4) и (2.7), длина Релея для главных осей пучка может быть найдена следующим образом:
, 
(2.8)
Таким образом, диаметры 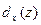и произвольного лазерного пучка в любой плоскости z полностью описываются шестью параметрами: 
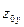, , для направления x и , , для направления y.