Геометрическая вероятность. Статистическое и аксиоматическое определения вероятности.

1. Геометрическая вероятность. Классическое определение ве­роятности предполагает, что число всех элементарных событий ко­нечно. Но на практике часто встречаются опыты, для которых мно­жество таких событий бесконечно. Например, пусть на отрезке [0; 1] числовой прямой ставят наудачу точку. Что подсказывает нам ин­туиция о вероятностях событий «точка попала на правую половину отрезка» и «точка попала на левую половину отрезка»? Поскольку точка ставится наудачу, то естественно считать эти события равно­вероятными — вероятность каждого 0,5 (поскольку это противопо­ложные события). Ну, а если мы разделим отрезок на 10 равных отрезков и рассмотрим события «точка попала на левый отрезок», «точка попала на второй слева отрезок»,..., «точка попала на пра­вый отрезок»? Это опять равновероятные события. А вероятность каждого из них оказывается равной 0,1, поскольку это совокуп­ность всех элементарных событий нашего опыта. Поставим теперь вопрос: «Какова вероятность попадания точки на отрезок [0,3; 0,7]?» Поскольку этому событию благоприятствуют четыре из указанных выше элементарных события, то искомая вероятность равна 0,4, т. е. длине отмеченного отрезка. В общем случае смысл выражения «точка поставлена наудачу на отрезок длины l » состоит в том, что вероятность попадания точки на часть этого отрезка длины l равна этому числу l(если вместо отрезка [0; 1] взять отрезок [0; s], s>1, то искомая вероятность будет равна 1/s ).

Аналогично уясняется смысл выражения «точка поставлена наудачу в квадрат со стороной 1 (или в прямоугольник площадью 1)»,— это значит, что вероятность попадания точки на любую часть этого квадрата (или прямоугольника) равна площади этой части.

В более сложных случаях (на плоскости) может оказаться, что при геометрической интерпретации получится такая картина: име­ется фигура площадью s, и на нее наудачу ставится точка. Тогда вероятность попадания точки на часть этой фигуры, имеющую площадь q, оказывается равной q/s.

Аналогично в трехмерном случае (в пространстве) здесь берется отношение соответствующих объемов. Такое определение вероятно­сти получило название геометрического.

Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности — вероятности попадания точки в область (отрезок, часть плоскости и т. д.).

Пример. В окружность вписан квадрат. В круг наудачу ставят точку. Какова вероятность того, что эта точка попадет в квадрат?

Событие А – точка попадает в квадрат

Отношение площадей квадрата и круга дает искомую вероят­ность:

P(А) = , где S­_1­ = а² (площадь квадрата), S­_2­ =pR² (площадь круга).

P(А) = = = .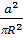

2. Относительная частота. Статистическое определение вероятно­сти. Классическое определение вероятности оказывается непригод­ным для изучения произвольных случайных событий. Так, оно неприемлемо, если результаты испытания не равновозможны. На­пример, при бросании неправильной игральной кости выпадение ее различных граней не равновозможно.

В таких случаях используется так называемое статистическое определение вероятности.

Пусть произведено п испытаний, при этом некоторое собы­тие А наступило т раз.

Определение 1. Число т называется абсолютной частотой (или просто частотой) события А, а отношение

P*(A)= .

называется относительной частотой события А.

Пример 1. При транспортировке из 10000 арбузов испорти­лось 26. Здесь т = 26 — абсолютная частота испорченных арбузов, а

P*(A)= 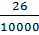= 0,0026.

относительная.

Результаты многочисленных опытов и наблюдений, многие из которых описаны, например, в работах [1—4], помогают заключить: при проведении серий из nиспытаний, когда число nсравнительно мало, относительная частота Р*(А)принимает значения, которые могут довольно сильно отличаться друг от друга. Но с увеличени­ем n — числа испытаний в сериях — относительная частота

Р*(А) = .

приближается к некоторому числу Р(А), стабилизируясь возле него и принимая все более устойчивые значения.

Пример 2. Было проведено 10 серий бросаний монеты, по 1000 бросаний в каждой. Относительные частоты выпадения герба оказались равными 0,501; 0,485; 0,509; 0,536; 0,485; 0,488; 0,500; 0,497; 0,494; 0,484. Эти частоты группируются около числа 0,5.

Определение 2 (статистическое определение вероятности). Вероятностью события Ав данном испытании называется число Р(А), около которого группируются значения от­носительной частоты при больших n в различных сериях испытаний.

В условиях только что приведенного примера указанная вероят­ность равна 0,5.

Пример 3. По данным шведской статистики, относительные частоты рождения девочек по месяцам одного года характеризуют­ся следующими числами (расположены в порядке следования ме­сяцев, начиная с января): 0,486; 0,489; 0,490; 0,471; 0,478; 0,482; 0,462; 0,484; 0,485; 0,491; 0,482; 0,473. Эти частоты груп­пируются около числа 0,482.

Таким образом, относительная частота события приближенно со­впадает с его вероятностью, если число испытаний достаточно велико. Имеется огромный опытный материал по проверке последнего утверж­дения. Приведем еще один такой пример с бросанием монеты.

Здесь относительные частоты незначительно отличаются от чис­ла 0,5, причем тем меньше, чем больше число испытаний. При 4040 испытаниях отклонение равно 0,008, а при 24 000 — 0,0005.

Таким образом, относительная частота события приближенно совпадает с его вероятностью в статистическом смысле, если число испытаний достаточно велико.

С этой точки зрения величина m=npпредставляет собой сред­нее значение числа появления события Aпри nиспытаниях.

При широких предположениях доказывается, что вероятности события в классическом и статистическом смысле совпадают между собой.

3. Аксиоматическое определение вероятности. В современных ма­тематических курсах вероятность определяется аксиоматически. При аксиоматическом построении теории вероятностей исходят из свойств вероятности событий, к которым применимо классическое или ста­тистическое определение. Отдельные свойства вероятности извест­ны из предыдущую изложения. Поэтому естественно принять сле­дующие аксиомы.

Аксиома 1. Каждому событию А поставлено в соответствие неотрицательное число Р(А), называемое его вероятностью.

Аксиома 2. Вероятность достоверного события равна единице.

Аксиома 3. Вероятность суммы попарно несовместимых собы­тий равна сумме вероятностей этих событий.

Последняя аксиома называется аксиомой сложения вероятностей.

Исходя из этих аксиом, свойства вероятностей и зависимости между ними выводят в качестве теорем.

1. Известно, что электронный луч попал в мишень радиуса R. Какова вероятность, того что он отклонился от центра не более чем на r?

Решение:

Площадь все области: мера(G) = S = p 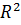, площадь области, отвечающей событию А: мера(g) = s = p поэтому, используя, находим P(A) = .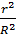

2. Оценить вероятность появления признака А, если в серии из 500 испытаний этот признак наблюдается 20 раз.

Решение: В качестве оценки вероятности принимаем относительную частоту W(A) = 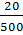= 0,04.

3. Какова вероятность того, что сумма двух положительных чисел меньше 1, если каждое в отдельности не превышает 1?

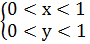, y < 1 – x, x + y < 1, x ≤ 1, y ≤ 1.

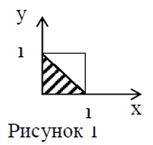
Решение: Первое число xÎ(0;1], аналогично второе число yÎ(0;1]. Общее пространство G, как видно из рисунка 1, представляет событию А, есть заштрихованный треугольник (s=0,5). Поэтому P(A) = s/S = 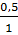= 0,5.(ε-окрестность целиком принадлежит области G).

Вопросы:

1. Дайте определение геометрической вероятности?

2. Сформулируйте определение абсолютной частоты?

3. Сформулируйте определение относительной частоты?

4. Дайте определение статистической вероятности?

5. Сформулируйте аксиомы вероятности?

Урок №2.

Вариант 1.

1. Отдел технического контроля обнаружил в партии из 1000 изделий 20 бракованных. Найти частоту изготовления бракованного изделия.

2. После бури на участке между 40-м и 70-м километрами телефонной линии произошел обрыв провода. Какова вероятность того, что разрыв произошел между 45-м и 50-м километрами линии?

Вариант 2.

1. При испытании партии приборов частота появления годных приборов составила 0,7. Найти число годных приборов, если всего проверено 200 штук.

2. В круг радиуса r наудачу брошена точка. Найти вероятность того, что эта точка окажется внутри вписанного в данный круг правильного треугольника.

Вариант 1*.

1. В результате сдачи государственного экзамена частота получения «хороших» и «отличных» оценок оказалась равной 0,6. Сколько выпускников выдержало экзамен, если, кроме того, ими получено, 48 «неудовлетворительных» оценок?

2. На окружности радиуса r наудачу поставлены три точки A, B и C. Найти вероятность того, что треугольник ABC остроугольный.

Вариант 2*.

1. Найти число n выстрелов по цели, если частота попаданий оказалась равной p, а промахов было совершено k.

2. Двое договорились о встрече в определенном месте. Каждый из них приходит в условленное место независимо друг от друга в случайный момент времени из [0;T] и ожидает не более, чем время tÎ(0;T). Какова вероятность встречи на таких условиях?

Свойства вероятности