Случайные события. Классическое определение вероятности

Глава 1: «Случайные события»

Теория вероятностей изучает математические модели

случайных событий и позволяет по вероятностям одних

случайных событий находить вероятности других случайных

событий, связанных каким-либо образом с первыми.

Прохоров и Севастьянов

 

 

СЛУЧАЙНЫЕ СОБЫТИЯ И ВЕРОЯТНОСТИ

Случайные события. Классическое определение вероятности

1. Понятие о случайном событии. Опыт, эксперимент, наблюде­ние явления называют испытанием. Испытаниями, например, явля­ются: бросание монеты, выстрел из винтовки, бросание игральной кости (кубика с нанесенным на каждую грань числом очков — от одного до шести).

Результат, исход испытания называется событием. Событиями являются: выпадение герба или цифры, попадание в цель или промах, появление того или иного числа очков на брошенной игральной кости.

Для обозначения событий используются большие буквы латин­ского алфавита: А, В, С и т.д.

Определение 1. Два события называются совместимыми, если появление одного из них не исключает появление другого в одном и том же испытании.

Определение 2. Два события называются несовместимыми, если появление одного из них исключает появление другого в одном и том же испытании.

Пример 1. Испытание: однократное бросание игральной ко­сти. Событие А — появление четырех очков, событие В — появление четного числа очков. События А и В совместимые.

Пример 2. Испытание: однократное бросание монеты. Собы­тие А — выпадение герба, событие В — выпадение цифры. Эти со­бытия несовместимы, так как появление одного из них исключает появление другого.

Несовместимость более чем двух событий в данном испытании означает их попарную несовместимость.

Пример 3. Испытание: однократное бросание игральной ко­сти. Пусть события

А­₁, А₂, А₃, А₄, А₅, А₆— соответственно выпа­дение одного очка, двух, трех, четырех, пяти и шести очков. Эти события являются несо­вместимыми.

Определение 3. Два события А и В называются противопо­ложными, если в данном испытании они несовместимы и одно из них обязательно происходит.

Событие, противоположное событию А, обозначают через .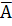

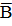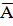Пример 4. Испытание: однократное бросание монеты. Собы­тие А — выпадение герба, событие В — выпадение цифры. Эти со­бытия противоположны, так как исходами бросания могут быть лишь они и появление одного из них исключает появление другого, т. е. А = или = В.

Определение 4. Событие называется достоверным, если в данном испытании оно является единственно возможным его исхо­дом, и невозможным, если в данном испытании оно заведомо не может произойти.

Пример 5. Испытание: извлечение шара из урны, в кото­рой все шары белые. Событие А — вынут белый шар — достовер­ное событие; событие В — вынут черный шар — невозможное со­бытие.

Заметим, что достоверное и невозможное события в данном ис­пытании являются противоположными.

Определение 5. Событие Аназывается случайным, если оно объективно может наступить или не наступить в данном испы­тании.

Пример 6. Событие А­₆ — выпадение шести очков при броса­нии игральной кости — случайное. Оно может наступить, но может и не наступить в данном испытании.

Пример 7. Событие А₉₈ — прорастание девяноста восьми зе­рен пшеницы из ста — случайное. Это событие может наступить, но, может быть, прорастет зерен больше или меньше.

 

Алгебра событий.

Определение 1. Суммой событий А и Вназывается событие С = А + В, состоящее в наступлении по крайней мере одного из со­бытий А или В.

Пример 1. Испытание: стрельба двух стрелков (каждый дела­ет по одному выстрелу). Событие А — попадание в мишень первым стрелком, событие В— попадание в мишень вторым стрелком. Сум­мой событий Аи В будет событие С = А + В, состоящее в попадании в мишень хотя бы одним стрелком.

Аналогично суммой конечного числа событий А­₁, А₂,..., А­_k­называется событие

А = А­₁ +А₂ +... + А_k, состоящее в наступлении хотя бы одного из событий А­_i (i=1,..., k).

Из определения 1 непосредственно следует, что А + В = В + А. Справедливо также и сочетательное свойство. Однако А + А = А(а не 2А, как в алгебре).

Определение 2. Произведением событий А и Вназывается событие С = АВ, состоящее в том, что в результате испытания про­изошли и событие А, и событие В.

Аналогично произведением конечного числа событий А­₁, А₂,..., А­_kназывается событие

А = А­_{1 ­}А­_{2 ­}… А­_k, состоящее в том, что в результате испытания произошли все указанные события.

В условиях предыдущего примера произведением событий А и Вбудет событие С = АВ, состоящее в попадании в мишень двумя стрелками.

Из определения 2 непосредственно следует, что АВ = ВА.

Справедливы также сочетательный и дистрибутивный законы. Однако АА = А (а не А²).

 

Сумма	Произведение
"А, А+А=А	А·А=А
"А,В, А+В=В+А	А·В=В·А
"А,В,С, (А+В)+С=А+(В+С)	(А·В) ·С=А·(В·С)
А+W=W	А·W=А
А+Æ=А	А·Æ=Æ
	(А+В) ·С=А·С+В·С

 

 

3. Классическое определение вероятности. Всякое испытание вле­чет за собой некоторую совокупность исходов — результатов испы­тания, т. е. событий. Во многих случаях возможно перечислить все события, которые могут быть исходами данного испытания.

Определение 1. Говорят, что совокупность событий обра­зует полную группу событий для данного испытания, если его ре­зультатом обязательно становится хотя бы одно из них.

Примеры полных групп событий — выпадение герба и выпаде­ние цифры при одном бросании монеты; попадание в цель и про­мах при одном выстреле; выпадение одного, двух, трех, четырех, пяти и шести очков при одном бросании игральной кости.

Рассмотрим полную группу попарно несовместимых событий U­_1­, U­_2­, …, ­ U­_n­, связанную с некоторым испытанием. Предположим, что в этом испытании осуществление каждого из событий U­_i­­ (i=1, 2,…, n) равновозможно, т. е. условия испытания не создают преимуществ в появлении какого-либо события перед другими возможными.

Определение 2. События образующие пол­ную группу попарно несовместимых и равновозможных событий, называют элементарными событиями.

Пример 1. Вернемся к опыту с подбрасыванием игральной кости. Пусть V, — событие, состоящее в том, что кость выпала гранью с цифрой. Как уже отмечалось, события

U­_1­, U­_2­, …, U_n образуют полную группу попарно несовместимых событий. Так как кость предполагается однородной и симметричной, то собы­тия U­_1­, U­_2­, …, ­ U­₆ являются и равновозможными, т. е. элементар­ными.

 

Определение 3.

Событие А называется благоприятствую­щим событию В, если наступление события А влечет за собой на­ступление события В.

Пример 2. Пусть при бросании игральной кости события U­₂, U­_4­ и U­_6­— появление соответственно двух, четырех и шести очков, а А — событие, состоящее в появлении четного числа очков; собы­тия U­₂, U­_4­ и U­_6­ благоприятствуют событию А.

Определение 4 (классическое определение ве­роятности).

Вероятностью Р(А)события Аназывается отноше­ние числа испытаний в которых событие наступилок числу всех испытаний, т. е.

Р(А) = m/n.

Пример 3. Вычислим вероятность выпадения герба при од­ном бросании монеты. Очевидно, событие А — выпадение герба — и событие В— выпадение цифры — образуют полную группу несов­местимых и равновозможных событий для данного испытания. Значит, здесь n = 2. Событию А благоприятствует лишь одно собы­тие—само А, т.е. здесь m=1. Поэтому Р(А) =1/2.

Пример 4. Очевидно, что при одном бросании игральной кости (вероятность выпадения какой-либо цифры от 1 до 6 будет равна

P(U­_i­) = 1/6, i=1, 2,..., 6.

Пример 5. Найдем вероятность того, что при однократном бросании игральной кости выпадет число очков, делящееся на 2 (событие А).

Число элементарных событий здесь(n) 6. Число благоприятствую­щих элементарных событии(m) 3 (выпадение 2, 4 и 6). Поэтому

P(A)=m/n, P(A)= = .

Пример 6. При составлении команды космического корабля возникает вопрос о психологической совместимости отдельных членов экипажа. Допустим, что надо составить команду из трех человек: командира, инженера и врача.

 

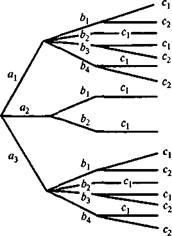На место командира есть три кандидата: а­₁, а­₂, а₃; на место инженера — четыре кандидата: b_1­­, b₂, b₃, b₄; на место врача — два кандидата: с­₁, с₂. Проведенная проверка показала психологическую несовместимость командира а₂ с инженерами b₃, b₄ и с врачом c­₂, а также инженера b ₂ с врачом ­­c­₂. Будем для простоты считать, что без учета фактора несовместимо­сти все варианты составления коман­ды равновозможны. Какова в этом случае вероятность того, что будет составлен экипаж, все члены которо­го психологически совместимы друг с другом?

Представим все варианты команды, при которых члены экипажа совмес­тимы друг с другом в виде «дерева» (рис. 1). Число ветвей этого дерева, т. е. исходов, благоприятствующих собы­тию А, равно 16, а общее число воз­можных комбинаций по правилу рис 1. про­изведения равно 4 · 3 · 2 = 24. Искомая вероятность Р(А) = 16/24 = 2/3.

 

Задача (Вероятности рождения мальчиков и девочек). Будем предпо­лагать, что случаи рождения мальчика и девочки — равновозможные события.

Пусть в семье двое детей. Какова вероятность, что оба ребен­ка — мальчики? Если известно, что один мальчик, какова вероят­ность, что оба ребенка — мальчики?

На первый вопрос ответить нетрудно. Имеется четыре равновозможных исхода: ММ, МД, ДМ, ДД ( М — мальчик, Д— Девочка). Исходы МДи ДМразличны, так как в первом из них сначала родился мальчик, а потом девочка, во втором — наоборот. Из этих четырех исходов только один ММ благоприятствует нашему событию. Отсюда следует, что Р(ММ) = 1/4.

Если дополнительно известно, что один ребенок — мальчик, то событие ДДисключается. Из трех равновозможных событий ММ, МД, ДМ по-прежнему только одно ММблагоприятствует желаемому исходу. Поэтому Р(ММ) = 1/3.

Если известно, что старший ребенок — мальчик, то исключаются исходы ДМ и ДД. В этом случае Р(ММ) =1/2.

Из приведенного классического определения вероятности выте­кают следующие ее свойства:

1. Вероятность достоверного события равна единице.

Действительно, достоверному событию должны благоприятство­вать все п элементарных событий, т. е. т = п и, следовательно,

P(A)=m/n=n/n=1.

2. Вероятность невозможного события равна нулю. В самом деле, невозможному событию не может благоприятст­вовать ни одно из элементарных событий, т.е. т = 0, откуда

P(A)=m/n=0/n=0.

3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных событий. Поэтому в этом случае 0<m<n и, значит, 0<m/n<1. Следовательно, 0<Р(А)<1.

Таким образом, вероятность любого события удовлетворяет двой­ному неравенству

Замечание. Из определения вероятности следует, что эле­ментарные события являются равновероятными, т. е. обладают од­ной и той же вероятностью.