Комбинаторика — раздел математики, занимающийся вопросами о том, сколько комбинаций определенного типа можно получить из данных предметов (элементов). Как при решении задач с использованием классического определения вероятности, так и в дальнейшем могут нам понадобиться некоторые определения и формулы комбинаторики. Приведем наиболее употребительные из них.
Определение 1. Размещениями из nразличных элементов по т элементов ( m ≤ n ) называются комбинации, составленные из данных nэлементов по т элементов, которые отличаются либо самими элементами, либо порядком элементов.
Например, из трех элементов а, b, сможно составить по два элемента следующие размещения:
аb, ас, bс, bа, са, сb.
Число  размещений из n элементов а1, а2,..., an по mравно
размещений из n элементов а1, а2,..., an по mравно
 = n(n-1)(n-2)…(n-m+1) (1.1)
= n(n-1)(n-2)…(n-m+1) (1.1)
Пусть aα1, aα2,..., aαm(1 < αk ≤ п; k= 1,..., m) — всевозможные размещения, содержащие mэлементов. Будем эти размещения строить последовательно. Сначала определим aα1 — первый элемент размещения. Очевидно, из данной совокупности n элементов его можно выбрать n различными способами. После выбора первого элемента aα1 для второго элемента aα2 остается n -1 способов выбора и т. д. Так как каждый такой выбор дает новое размещение, то все эти выборы можно свободно комбинировать между собой. Поэтому общее число размещений равно указанному произведению (1.1).
Пример 1. Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2?
Искомое число сигналов  =
=  ,
, 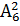 =6 · 5 = 30.
=6 · 5 = 30.
Определение 2. Перестановками из n различных элементов называются размещения из этих nэлементов по n.
Перестановки можно рассматривать как частный случай размещений при m = n, поэтому общее число перестановок из n элементов равно
Pn =n(n-1)(n-2)…3·2·1= n! (1.2)
Пример 2. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз?
Искомое количество трехзначных чисел P3 = 3! = 1·2·3 = 6.
Определение 3. Сочетаниями из n различных элементов по mэлементов называются комбинации, составленные из данных n элементов по m элементов, которые отличаются хотя бы одним элементом.
Отметим разницу между сочетаниями и размещениями: в первых не учитывается порядок элементов.
Обозначим через  число сочетаний из n элементов по m.
число сочетаний из n элементов по m.
Рассмотрим все допустимые сочетания элементов aα1, aα2,..., aαm. Делая в каждом из них m! возможных перестановок их элементов, очевидно, получим общее число размещений из nэлементов по m. Таким образом  ·m! =
·m! =  отсюда
отсюда
 =
=  =
=  (1.3)
(1.3)
Формулу (3) можно представить также в виде
 =
= 
 обладает очевидной особенностью
обладает очевидной особенностью  =
= 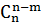
которая также верна и при т = 0, если принять 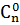 = 1. Этой особенностью удобно пользоваться, когда т > 1/2. Числа
= 1. Этой особенностью удобно пользоваться, когда т > 1/2. Числа  являются коэффициентами в формуле бинома Ньютона
являются коэффициентами в формуле бинома Ньютона
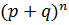 =
=  +
+ 
 q+
q+ 
 q2+…+ qn
q2+…+ qn
и поэтому часто называются биномиальными коэффициентами.
Свойства числа сочетаний:
1.  .
.
2.  .
.
3.  .
.
4.  .
.
Пример 3. Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей?
Используем формулу  =
=  ,
,  =
=  =
=  = 45.
= 45.
При решении задач комбинаторики можно использовать следующие правила:
Правило суммы. Если некоторый элемент А может быть выбран из совокупности элементов т способами, а другой элемент В — п способами, то выбрать либо А, либо В можно т + п способами.
Правило произведения. Если элемент А можно выбрать из совокупности элементов т способами и после каждого такого выбора элемент В можно выбрать п способами, то пара элементов (А, В) в указанном порядке может быть выбрана т·п способами.
Правила суммы и произведения естественным образом обобщаются и на случай комбинаций многих элементов, а именно, если первый элемент совокупности из k различных элементов можно выбрать n1 способами, второй – n2 способами и так далее, k-ый элемент – nk способами, то всевозможных комбинаций соответственно n1+n2+…+nk и n1·n2·…·nk
Приведем примеры применения формул комбинаторики к нахождению вероятностей событий.
Пример 4. Набирая номер телефона, абонент забыл две последние цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Какова вероятность того, что номер набран правильно?
Опыт: набор номера телефона.
Событие А – цифры набраны правильно.
Тогда число всевозможных исходов равно числу двузначных чисел, составленных из различных цифр. Так как в этом случае мы имеем выборку без возвращения (цифры различны), но упорядоченную (меняя цифры местами, получаем новое число), то n=  =10·9=90.
=10·9=90.
Исход, благоприятствующий наступлению события А только один.
P(А) =  =
=  =
=  @ 0,011.
@ 0,011.
Пример 5. Партия из 10 деталей содержит одну нестандартную. Какова вероятность, что при случайной выборке 5 деталей из этой партии все они будут стандартными (событие A)?
Здесь число всех случайных выборок и n = 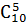 , а число выборок, благоприятствующих событию А, есть т =
, а число выборок, благоприятствующих событию А, есть т =  . Таким образом, искомая вероятность
. Таким образом, искомая вероятность
P(A) =  =
=  =
=  =
=  =
=  =
=  = 0,5.
= 0,5.
Пример 6. (Задача о Генуэзской лотерее*). Разыгрывается 90 номеров, из которых выигрывают пять. По условию можно ставить ту или иную сумму на любой из 90 номеров или на любую совокупность двух, трех, четырех или пяти номеров. Если участник лотери ставил на один номер, то он получал при выиграше в 15 раз больше ставки; если на два номера (амбо), то в 270 раз больше; если на три номера (терн), то в 5500 раз больше, если на четыре номера (катерн) — в 75 000 раз больше; если на пять номеров (квин) — в 1 000 000 раз больше, чем ставка. Какова вероятность выигрыша в каждом из указанных пяти случаев?
В первом случае вероятность выигрыша оказывалась
P1 = 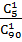 =
=  =
=  @ 0,055,
@ 0,055,
во втором, третьем, четвертом и пятом случаях вероятности выигрыша были соответственно равны:
P2 =  =
=  =
=  @ 0,0025,
@ 0,0025,
P3 =  =
=  =
=  @ 8,5
@ 8,5  10-5,
10-5,
P4 = 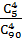 =
=  =
=  @ 1,9
@ 1,9  10-6,
10-6,
P5 =  =
=  =
=  @ 2,3
@ 2,3  10-8.
10-8.
Вопросы:
1. Дайте определение испытания?
2. Дайте определение события?
3. Дать определение двух совместных событий?
4. Дать определение двух не совместных событий?
5. Дать определение двух случайных событий?
6. Что называют суммой событий, произведение событий?
7. Сформулируйте определение полной группы событий?
8. Какие события являются элементарными, благоприятствующими?
9. Сформулируйте классическое определение вероятности?
10. Перечислите свойства, вытекающие из классического определения вероятности?
11. Сформулируйте определения размещение, перестановкой, сочетанием?
12. Сформулируйте правило суммы, правило произведения?
Урок №1 приведен как пример в Главе 1.