КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.
При выборе m элементов из n различных элементов говорят, что они образуют Соединение из n элементов по m. Различают три вида соединений элементов:
1. Размещениями называются соединения, которые отличаются друг от друга составом элементов или их порядком, и каждое из которых содержит m элементов, взятых из n различных элементов.
Например, выпишем все размещения элементов a, b, c, d по два: ab, ba, ac, ca, ad, da, bc, cb, bd, db, cd, dc.
2. Перестановками из n элементов называются соединения, каждое из которых содержит n различных элементов, взятых в определенном порядке.
Например, выпишем все перестановки из элементов a, b, c: abc, acb, bac, bca, cab, cba.
3. Сочетаниями из n элементов по m называются соединения, отличающиеся друг от друга, по крайней мере, одним элементом, каждое из которых содержит m элементов, взятых из n различных элементов.
Например, выпишем все сочетания из элементов a, b, c, d, e по три: abc, abd, abe, acd, ace, ade, bcd, bce, bde, cde.
Задача о числе размещений: Сколькими способами можно выбрать и разместить по m различным местам n разных предметов? Количество таких способов обозначается 
и читается: «Число размещений из n по m ».
, 
(по определению)
Пример 1. Сколько всего пятизначных телефонных номеров, в каждом из которых ни одна цифра не повторяется?
Решение. Это задача о выборе и размещении по пяти разным местам пяти из десяти различных цифр. Поэтому число указанных телефонных номеров равно 
.
Задача о числе перестановок: Сколькими способами можно переставить n разных предметов, расположенных на n разных местах? Количество таких способов обозначается 
и читается: «Число перестановок из n ».
, 
(по определению)
Пример 1. Сколько всего шестизначных четных чисел можно составить из цифр 1, 3, 4, 5, 7, 9, если в каждом из этих чисел ни одна цифра не повторяется?
Решение. Из всех указанных цифр последней может быть только цифра 4. Остальные пять цифр могут стоять на оставшихся пяти местах в любом порядке. Значит, нужно найти число перестановок из пяти элементов. 
. Таким образом, можно составить 120 указанных чисел.
Задача о числе сочетаний: Сколькими способами можно выбрать m из n разных предметов? Количество таких способов обозначается 
и читается: «Число сочетаний из n по m ».
; 
; 
.
Пример 1. Сколькими способами читатель может выбрать две книжки из пяти имеющихся?
Решение. Искомое число способов равно числу сочетаний из пяти по два. Так как 
, то указанную выборку читатель может осуществить десятью способами.
Правило сложения
Если некоторый предмет 
может быть выбран из совокупности предметов 
способами, а другой предмет 
может быть выбран 
способами, то выбрать либо , либо можно 
способами. Правило распространяется на совокупность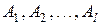 
.
Правило умножения
Если некоторый предмет можно выбран из совокупности предметов способами и после каждого такого выбора предмет может быть выбран способами, то пара объектов (, ) в указанном порядке может быть выбрана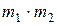 
способами. Правило распространяется на совокупность .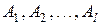