Требуется провести статический анализ механизма, определить значение массы m 3гр, при которой возможно равновесие системы. Найти усилия в тросе, соединяющем колеса 1 и 2 а также в тросе, на котором висит груз 3, определить реакции внешних опор колес. Сравнивая массы m3гр и массу m3, данную в условии, установить направление движения звеньев механизма.
1
S1
N2y S2 N1y
N2x m1g N1x
m2g
m3g Р
Рис.2 Статическая схема механизма
.
Для решения рассматривается равновесие каждого звена под действием сил, показанных на рисунке. Здесь mg-силы тяжести; Nx ‘, Ny-реакции подшипников; S1 и S2- силы действия и противодействия в тросе, соединяющем звенья 1 и 2. S1=S2.
Уравнения равновесия для звена 1:
Σ Fix=0 N1x - S1 cos15° =0; (2.1)
Σ Fiy=0 N1y - m1 g-S1sin15°–P =0; (2.2)
Σ Mо1(Fi) = 0 -P R1 + S1 r1 =0. (2.3)
Для колеса 2 с грузом 3
Σ Fix=0, N2x + S2 cos15° = 0; (2.4)
Σ Fiy=0, N2y – m2 g+ S2sin15° – m3 g =0; (2.5)
Σ Mo1(Fi) = 0, S2 r2 – m3 g R2 =0. (2.6)
Из (2.3) S2=S1= P R1 / r1=3500∙0,5/0,2=8750 H. Тогда из (2.6) m3g=S2 r2 / R2=8750∙0,3/0,4=6562,5 Н, отсюда m3гр = 669,643кг.
Определим реакции опор из остальных уравнений. Из (2.1) и(2.2)
N1x=8451,9 Н, N1y= 8207,5 Н, N2x=-8451,5 Н, N2y=4658,5 Н.
В равновесии натяжение троса, на котором висит груз, равно весу груза S3=m3 g =4905 H.
Сравнивая заданную массу m3=500кг массой m3гр, видим, что m3< m3гр, значит сила Р будет поднимать груз 3.
КИНЕМАТИКА МЕХАНИЗМА
Требуется установить кинематические зависимости, выразив кинематические параметры тел 2 и 3 через параметры тела 1.
ω1 ε1 φ1
δφ1
ε2 φ2
ω2
δφ2
а3
v3 1
y3
δy3 3 Рис.3 Кинематическая схема
На рисунке введены обозначения: ω1, ε1, φ1- угловая скорость, угловое ускорение, угловое перемещение тела 1; ω2 ε2 φ2-то же для тела 2; v3, a3, y3- линейная скорость, ускорение и перемещение тела 3.
Движение от тела 1 к телу 2 передается тросом и скорости точек, лежащих на окружностях колес малого радиуса, равны, ω1 r1=. ω2 r2. отсюда
ω2= ω1 r1 / r2, ω2=2/3 ω1. (3.1)
Касательные ускорения этих точек тоже равны, r2 ε2= r1 ε1.
ε2= r1 ε1 / r2, ε2=2/3 ε1. (3.2)
Равны и линейные перемещения этих точек, r2 φ2= r1 φ1:
φ2= r1 φ1 / r2, φ2=2/3 φ1. (3.3)
Груз 3 висит на тросе, который намотан на колесо радиуса R2, поэтому
v3 = R2 ω2, а с учетом (3.1):
v3= ω1 r1 R2 / r2, v3=0,2667 ω1. (3.4)
Ускорение груза 3 равно касательному ускорению точки, которая принадлежит большой окружности колеса 2, a3= ε2 R2. С учетом (3.2):
a3= r1 ε1 R2 / r2, a3=0,2667 ε1. (3.5)
Линейные перемещения груза 3 и точки на окружности радиуса R2 равны
y3= φ1 r1 R2 / r2, y3=0,2667 φ1. (3.6)
Формулы, полученные в этом параграфе, будут использоваться в дальнейших вычислениях.
4. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ДВИЖЕНИЯ МЕХАНИЗМА
Требуется составить динамическое дифференциальное уравнение движения механизма, приведя его к 1-ому телу, применяя теорему об изменении кинетической системы в дифференциальной форме.
По теореме об изменении кинетической энергии в дифференциальной форме, производная по времени от кинетической энергии механической системы равна сумме мощностей всех сил, действующих на систему
dT/dt= Σ NFi. (4.1)
Система состоит из твердых тел, тросы, передающие движение от одного тела к другому нерастяжимые и невесомые, поэтому сумма мощностей всех внутренних сил системы равна нулю.
Вычисление кинетической энергии механизма выполняется с учетом формул, полученных в главе 3. Кинетическая энергия системы равна сумме кинетических энергий всех звеньев, участвующих в движении
Т=Т1+Т2+Т3.
Тела 1 и 2 вращаются вокруг неподвижных осей, поэтому их кинетическая энергия вычисляется по следующим формулам:
Т1=Iz1 ω12 / 2;
Т1=Iz2 ω22 / 2.
Тело 3 движется поступательно, поэтому Т3=m3v32 / 2. Iz1 - момент инерции тела 1 относительно его оси вращения, он равен Iz1=m1 iz12=15,625кгм2. Iz2- момент инерции тела 2 относительно его оси вращения, он равен Iz2=m2 iz22= 18 кг м2.
С учетом формул (3.1)-(3.6) получается выражение для кинетической энергии
T= m1 iz12 ω12 / 2 + m2(iz2 r1 ω1)2 / 2 r22 + m3(r1 R2 ω1)2 / 2 r22
или T=(m1 iz12+ m2 iz22 r12/ r22+ m3r13 R22 / r22) ω12 / 2;
Т=(250∙0,42+200∙0,32∙0,22 / 0,32+500∙0.22∙0,42 / 0,32)ω12/2;
T=84ω12/2. (4.2)
dT/dt=84ω1ε1.
Для заданной механической системы, состоящей из твердых тел, соединенных нерастяжимыми, невесомыми тросами мощность всех внутренних сил равна нулю, поэтому необходимо вычислить мощность внешних сил.
В общем случае мощность силы определяется формулой N=F v cosα, где F=величина силы, v-скорость точки приложения силы, α - угол между направлением силы и направлением скорости. Силы тяжести тел 1 и 2, а также реакции опор N1x, N1y, N2x, N2y приложены к неподвижным точкам О1 и О2 поэтому их мощности равны нулю (см. рисунок в гл.4). Мощность силы Р равна
Np=Р R1∙ω1,
мощность силы тяжести m3g равна
N m3 g = -m3g v3.
Мощность пары сил, действующей на вращающееся тело, вычисляется как взятое со знаком + или – произведение момента пары на угловую скорость тела, поэтому мощность момента сил сопротивления вычисляется по формуле NМс= -Мс ω2
Сумма мощностей всех внешних сил с учетом формул п.3 равна
Σ NFi= Np+ N m3 g+ NМс= ω1(Р R1-Mc r1/r2-m3g r1 R2/ r2)ω1
Σ NFi =(Р R1-Mc r1/r2-m3g r1 R2/r2)ω1. (4.3)
Подстановка заданных величин позволяет вычислить суммарную мощность.
Пример для вариантов(1-60)*:
Σ NFi = (3500· 0,5-60∙(0,2)2/(0,3)2 ω1-500·10·0,2·0,4/0,3) ω1=(416,67-26,67 ω1) ω1;
Σ NFi =(416,67-26,67 ω1) ω1. (4.4)
Уравнение (12.1) имеет вид
84 ε1=416,67-26,67 ω1.
Дифференциальное уравнение движения имеет вид
+ 0,312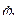 
=4,987. (4.5)
ω1
ω2
N2y N1y
N2x N1x
Mc P
V3
m3 g
Рис.4 Динамическая схема к вычислению мощностей сил
Замечание: приводимый расчет и составленное дифференциальное уравнение соответствует иар.1-60. Пример расчёта для вариантов 61-100 см. на стр.
Пример для вариантов 61-100:
Σ NFi = (3500· 0,5-60∙(0,2)2/(0,3)2 ω1-500·10·0,2·0,4/0,3) ω1=(416,67-26,67 ω1) ω1;
Σ NFi =(416,67-26,67 ω1) ω1. (