Задание 3. Исследование кинематики кривошипно-ползунного

Механизма

 

Определить скорость и ускорение точек А,В и С а также угловую скорость и угловое ускорение шатуна кривошипно-ползунного механизма в положении, определяемом углом φ между кривошипом и осью, параллельной оси движения ползуна.

1)Скорости точек В и С и угловые скорость шатуна АВ определить c помощью теоремы о распределении скоростей при плоском движении тела. Аналогично ускорения точек В и С и угловое ускорение шатуна определить c помощью теоремы о распределении ускорений.

Для всех вариантов принять следующие исходные данные: ОА=20см, АВ=100см, ω_ОА=2рад/с_. Значение угла φ и h выбрать из таблицы1, в соответствии с вариантом.

Решение выполнить графическим методом.

 

Варианты 1-30

№вар
φ,град
h,см
№вар
φ,град
h,см
№вар
φ,град
h,см

 

Варианты 1-15

А

С

φ В

О h

 

Варианты 16-30

 

А

 

 

О φ С

 

h

 

В

 

 

Варианты 31-60

№вар
φ,град
h,см
№вар
φ,град
h,см
№вар
φ,град
h,см

Варианты 31-45 Варианты 46-60

 

Варианты 61-100

№вар
φ,град
h,см
№вар
φ,град
h,см
№вар
φ,град
№вар
φ,град
h,см

 

 

Варианты 61-75

			φ

 

Варианты 76-100

 

 

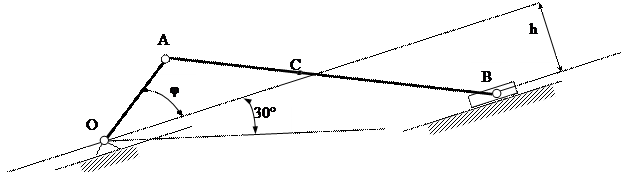
Пример. Определить скорости и ускорения точек А, В, С кривошипно-ползунного механизма в положении, указанном на рис.1. Дано ОА=20см, АВ=50см, φ=60, АС=20см.

ω_ОА=2с^-1, h=4см.

 

Рис.1 Схема механизма.

 

Решение. Для определения скоростей точек применяется теорема о распределении скоростей точек при плоскопараллельном движении твердого тела. Согласно этой теореме, скорость любой точки шатуна равна векторной сумме двух скоростей: вектора скорости какой-нибудь точки, взятой за полюс, и скорости этой точки во вращательном движении вокруг этого полюса

V _B= V _A+ V _BA; (1)

С

V _C= V _A+ V _CA. (2)

 

VA

А   А

В формулах (1) и (2) V _A-вектор* скорости точки А, который перпендикулярен кривошипу ОА и равен по величине V_А= ω_ОА∙ОА=2∙20=40см/с.

 

Рис.2 Кинематика

 

 

 

Масштаб m_v=1 см/с/мм

 

Рис.3 Графическое определение скоростей точек.

 

Вектор скорости точки В горизонтален и по величине неизвестен. Вектор V _BA скорости точки В во вращательном движении шатуна АВ вокруг полюса А направляется перпендикулярно отрезку АВ (рис.2). На рис. 3 показано построение векторного треугольника, с помощью которого определяются все неизвестные скорости. Начинаем построение с отрезка Ра, который в масштабе m_v соответствует скорости V_А. Затем через точку а проводим линию перпендикулярную АВ, и через точку Р линию параллельную скорости V _B.

В получившемся треугольнике расставляем направления векторов так, чтобы выполнилось равенство (1). Модули неизвестных векторов получаем, измеряя их значения на рисунке. С учетом масштаба получим V_B=42см/с, V_BA=21.31см/с.

Определяем угловую скорость шатуна АВ:

ω_АВ= V_BA/ВА=21,31/50=0,407с^-1. (3)

Направление вращения шатуна - по часовой стрелке. Вычисляем скорость V_CA.

V_CA= ω_ab∙АС=0,407∙20=8,14см/с.

С учетом того, что скорость V _CA перпендикулярна отрезку СА и направлена в ту же сторону, что и V _BA, построим скорость V _C. Измеряя длину вектора V _C,получим его величину V_C=39см/с.

Перейдем к определению ускорений точек.

 

68,

Определение ускорений точек следует начинать с вычисления ускорения точки А. Кривошип ОА вращается равномерно, поэтому ускорение точки А совпадает с нормальным ускорением, которое направлено от точки А к точке О.

а_А=а_Аⁿ= ω_ОА²∙ОА=2²∙20=80см/с².

 

Ускорения точек В и С определяем с помощью теоремы о распределении ускорений в плоскопараллельном движении шатуна АВ. Согласно этой теореме вектор ускорения любой точки тела при его плоскопараллельном движении равен векторной сумме ускорения какой-нибудь другой точки, взятой за полюс, касательного и нормального ускорений рассматриваемой точки во вращательном движении тела вокруг полюса.

а _В= a _A +a _ba^τ+ a _baⁿ (4)

а _с= a _A +a _сa^τ+ a _сaⁿ (5)

При этом, величина касательного ускорения равна a_ba^τ=ε_ba∙BA, а направление перпендикулярно отрезку АВ; величина нормального ускорения равна a_baⁿ=(ω_ab)²∙BA, а направление параллельно отрезку ВА от В к А (см.рис.4).

На рис.5 показано графическое решение, соответствующее уравнению (4). На рис. а) показано начало построения в масштабе m=20см/с²/см. Из произвольной точки откладывается вектор. a _A,на рисунке он изображен отрезком ра. Определяется величина вектора a_baⁿ=(0,4070)²∙50=8,28см/с² и затем он пристраивается к вектору a _A. Через конец вектора a _baⁿ проводится линия перпендикулярная АВ, а через начало вектора a _A проводится линия параллельная ходу ползуна. Построение завершается расстановкой стрелок (см. рис.5 б).Все искомые величины измеряются и с учетом масштаба определяются.

a_b=19см/с²

a_ba^τ=68,54см/с²

ε_ba=1,37с^-2

По рис.5 можно установить, что ε_ba направлено против часовой стрелки.

Аналогично определяется ускорение точки С, величины слагаемых векторов вычисляются по формулам:

а_сaⁿ=(ω_ab)²∙СA

a_сa^τ=ε_ba∙СA

Величина ускорения а _с измеряется. а_с=44,98см/с².

Итог расчета представлен в таблице.

VB	VC	ab	ас	ωАВ	εba
42см/с	39см/с.	19см/с2	19см/с2	0,407с-1	1,37с-2

*В тексте вектор обозначен жирным шрифтом V -вектор скорости; обычным шрифтом величина вектора. V-величина скорости.