МОЩНОСТИ ВЕДУЩЕГО УСИЛИЯ

Ведущим усилием для рассматриваемого механизма является сила Р. Мощность силы Р вычисляется по формуле N_P=Pv cos0˚, где v-скорость точки приложения силы Р, 0˚-угол между направлением силы и скорости. Используя формулу (6.2), получим

V=ω₁·R₁= 15,984(1- е^{- 0,312t})0,5=7,992(1- е^{- 0,312t})м/с;

N_P=27972(1- е^{- 0,312t})Вт.

Максимальное значение мощность ведущего усилия имеет при установившемся движении N_P^max=27,972кВт.

10. РАБОТА СИЛЫР НА ПЕРЕМЕЩЕНИИ, СООТВЕТСТВУЮЩЕМ t_уст

Работа силы, приложенной к вращающемуся телу, вычисляется по формуле

А_Р= ,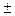

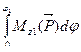где М_Z(P) -момент силы Р относительно оси вращения тела 1.

В нашем случае момент силы Р относительно оси вращения постоянен и равен М_z1=Р·R₁=1750 Нм, поэтому работу силы Р следует вычислять по формуле

А_Р=Р·R₁ φ₁.

Знак + выбран потому, что направление момента силы Р и направление вращения колеса 1 совпадают. Вычислим значение угла поворота φ₁для момента времени, за которое движение механизма устанавливается t_уст=15 c, по формуле (5.3)

φ₁(15)= 51,23(-1+ е^{- 0,312·15})+15,984·15 =29,165рад.

Искомое значение работы:

А_Р=1750·29,165=51039Дж=51,039кДж.

ОПРЕДЕЛЕНИЕ ЗНАЧЕНИЯ СИЛЫРmin.

Требуется, применяя принцип возможных перемещений, определить при коком значении силы Р_min груз 3 будет подниматься с маленькой скоростью.

Согласно принципу возможных перемещений для равновесия механической системы с идеальными связями, необходимо и достаточно, чтобы сумма элементарных работ всех действующих на нее активных сил при любом возможном перемещении системы была равна нулю.[1]

Σ δА_к=0.

Определим предельное значение силы Р, которая будет удерживать механизм в равновесии при заданных массах звеньев. Сопротивление, зависящее от скорости в этом случае равно 0.

На рисунке в главе 2 изображены активные силы, действующие на механизм, в случае его равновесия, возможные перемещения звеньев механизма δφ₁,δφ₂ и δy₃.

Рассматриваемая механическая система имеет одну степень свободы, связи, наложенные на систему, являются стационарными и голономными, поэтому зависимости между возможными перемещениями такие же, как между действительными перемещениями, определенными формулами (3.3), (3.6), (3.9).

δφ₂= r₁/r₂ δφ_1;

δy₃= r₁ R₂/r₂ δφ_1.

Дадим механизму возможное перемещение и вычислим возможную работу активных сил.

Σ δА_к = δА_Р+ δА_Мс+ δА_m1g;

Σ δА_к =РR₁ δφ₁-m₃g δy₃=0;

Σ δА_к =Р R₁ δφ₁ -m₃g r₁ R₂/r₂ δφ₁=0;

Р_min R₁ -m₃g r₁ R₂/r₂ =0.

Получаем значение искомой силы

Р_min = +m₃g r₁ R₂/r₂ R₁=533,33Н.

При значении силы немного больше Р_min=533,33Нгруз 3 будет подниматься с очень маленькой скоростью.

ВЫВОДЫ

Методами статики исследовано состояние равновесия подъемного механизма и установлена грузоподъемность, реакции внешних опор и сил натяжения тросов при максимальной нагрузке.

Исследована кинематика механизма и установлены зависимости между параметрами движения его звеньев.

Для исследования динамики движения механической системы был применен принцип Даламбера.

Получено дифференциальное уравнение движения механической системы, после интегрирования которого, установлены законы движения всех тел и получены формулы изменения их скоростей и ускорений.

Построены графики изменения параметров движения тела 1. По графику угловой скорости видно, что через некоторое время угловая скорость колеса 1 становится постоянной и равной ω_1уст=15,984с^-1, это значит, что движение устанавливается, и все тела движутся равномерно. Время установления t_уст= 15 c.

Определены силы натяжения тросов. Установлены законы изменения значений этих сил и определены их максимальные значения. Вычислены реакции внешних связей и их максимальные значения.

Установлена зависимость мощности ведущего усилия Р от времени и определено её максимальное значение N_р^мах=10,474кВт. Определена работа ведущего усилия на перемещении, соответствующем времени установления движения.

Принцип возможных перемещений применен для определения ведущего усилия Р, необходимого для подъема тела 3 с очень маленькой скоростью.

*Приведённый выше пример по ходу расчётов и по используемым формулам годится для всех вариантов. Но дифференциальное уравнение в вар. 61-100 получается иным. Чтобы показать отличие приводится пример для этих вариантов.

*Пример расчёта суммарной мощности и составление дифференциального уравнения движения механизма для вар.(61-100).

Будем составлять динамическое уравнение движения механизма, приведенного в предыдущем примере, если при сохранении всех данных изменить только значения ведущего усилия Р и момента сил сопротивления Мс. Возьмём Р=(3000+30t)Н и Мс=100Нм. Значение кинетической энергии остается таким же, как в предыдущем примере в параграфе 4:Т=84ω₁²/2. и dT/dt=84ω₁ε₁.

По формуле (4.3) вычисляем суммарную мощность.

Σ N_Fi =(Р R₁-M_c r₁/r₂-m₃g r₁ R₂/r₂)ω_1. (4.3)

Σ N_Fi = ((3000+30t) 0,5-100∙0,2/0,3 -500·10·0,2·0,4/0,3) ω₁=(100,7+15t) ω₁;(4.4)

По теореме dT/dt= Σ N_Fi. В нашем случае

84ω₁ε₁=(100,7+15t) ω₁.

Сокращая ω₁ и учитывая, что ε₁= 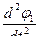, получим дифференциальное уравнение

84 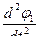=100,7+15t. (4.5)

Решение дифференциального уравнения.

Дифференциальное уравнение решается при нулевых начальных условиях, потому что механизм начинает двигаться из состояния покоя.

При t=0 φ₁₀=0 и ω₁₀=0. Перепишем уравнение (4.5) с учетом того, что 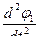= 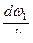, получим

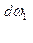=100,7+15t.

Умножим это уравнение на dt и проинтегрируем правую и левую части:

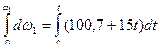
После интегрирования получим закон изменения угловой скорости по времени:

ω₁(t)=(100,7t+7,5t²)1/c

Заменим ω₁=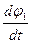

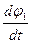=100,7t+7,5t², и проинтегрируем

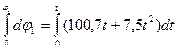
φ₁(t)=50,35t²+2,5t³.

Последняя формула определяет закон движения тела 1. Итак, мы установили законы изменения параметров движения тела 1 и его закон движения:

ε₁(t)=100,7+15t.

ω₁(t)=(100,7t+7,5t²)1/c

φ₁(t)=50,35t²+2,5t³

Вычислим значения ε₁, ω₁ и φ₁ в момент времени t=3c: ε₁(3)=115,7 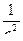, ω₁(3)=169,6 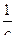, φ₁(3)=520,65радиан.

Дальнейшие расчеты необходимо продолжить по плану задания с помощью первого примера, с учетом полученного решения дифференциального уравнения.

Пример оформления титульного листа