Транспортная задача линейного программирования

Содержание

Линейная производственная задача 3

2. Двойственная задача 4

Задача о "расшивке узких мест производства" 6

3. Транспортная задача линейного программирования 7

4. Динамическое программирование. Распределение капитальных вложений 11

5. Анализ доходности и риска финансовых операций 13

6. Матричная игра как модель конкуренции и сотрудничества 15

7. Задача о кратчайшем пути 20

8. Задача о максимальном потоке в сети 21

Линейная производственная задача

Задача о рациональном использовании производственных мощностей является одной из первых задач, для решения которой были применены методы линейного программирования. В общем виде математическая модель задачи об использовании производственных мощностей может быть получена следующим образом.

Предприятие может использовать m групп ресурсов для выпуска n видов изделий. Известны нормы расхода ресурсов для выпуска каждого изделия и общий объем ресурсов, которые могут быть использованы для выпуска продукции в определенный период времени. Пусть, кроме того известна удельная прибыль на единицу продукции каждого вида. Требуется составить план производства, который обеспечивает получение максимальной суммарной прибыли за определенное время (месяц, квартал, год).

Примем следующие обозначения:

i – номер ресурса (i =1,2, …, m);

j – номер вида изделия (j =1,2, …, n);

a_ij – норма расхода ресурса вида j - на единицу i -го изделия;

b_i общий объем ресурса вида j, который может быть использован для выпуска продукции в определенный период времени;

с _j удельная прибыль на единицу j-го изделия.

Для построения формальной модели введем переменные x_i, значения которых будут показывать планируемое количество единиц j -го изделия. По смыслу задачи все переменные могут принимать только неотрицательные значения. Набор значений переменных (x₁, x₂, …, x_n) будет представлять искомый план производства.

 

Исходные параметры задачи представлены в виде технологической матрицы A затрат ресурсов на единицу продукции каждого вида, вектора B объемов ресурсов и вектора C удельной прибыли:

 

2 3 4 1 103

A = 4 2 0 2 B= 148 C= (36 32 10 13)

2 8 7 0 158

 

При этом x₁ ³ 0, x₂ ³ 0, x₃ ³ 0, x₄ ³ 0.

 

Составим функция прибыли (целевую функцию):

 

Z=36x₁+32x₂+10x₃+13x₄

Необходимо составить производственную программу (х₁, х₂, …, х_n) так, чтобы функция Z приняла наибольшее значение при выполнении всех других условий:

 

2 x₁ + 3x₂ + 4x₃ + 1x₄ £103 1 вид ресурса

4x₁ + 2x₂ + 0x₃ + 2x₄ £ 148 2 вид ресурса (1)

2x₁ + 8x₂ + 7x₃ + 0_x4 £ 158 3 вид ресурса

 

Неравенства (1) нужно превратить в равенства. Для этого вводим дополнительные неотрицательные неизвестные x₅ ³ 0, x₆ ³ 0, x₇ ³ 0.

Решим задачу с помощью симлексной таблицы:

 

 

			X1	X2	X3	X4	X5	X6	X7
c`	Базис	H
	X5
	X6
	X7
	Z-Z0		D1 = -36	D2 = -32	D3 = -10	D4 = -13	D5 = 0	D6 = 0	D7 = 0
	X5							-0.5
	X1			0.5		0.5		0.25
	X7					-1		-0.5
	Z-Z0		D1 = 0	D2 = -14	D3 = -10	D4 = 5	D5 = 0	D6 = 9	D7 = 0
	X5					0.29		-0.36	-0.29
	X1				-0.5	0.57		-0.29	-007
	X2					-0.14		-0.07	0.14
	Z-Z0		D1 = 0	D2 = 0	D3 = 4	D4 = 3	D5 = 0	D6 = 8	D7 = 2

 

Рассчитываем таблицу до тех пор пока все Dj не станут неотрицательными.

 

 

Двойственная задача

 

Ранее мы рассмотрели конкретную линейную производственную задачу по выпуску четырех видов продукции с использованием трех видов ресурсов по заданным технологиям.

Теперь представим себе, что возникла новая ситуация. Некий предприниматель, занимающийся производством каких-то других видов продукции, но с использованием трех таких же видов ресурсов, какие имеются у нас, предлагает нам "уступить" по определенным ценам все имеющиеся у нас ресурсы и обещает платить у₁ рублей за каждую единицу первого ресурса, у₂ руб – второго, у₃ руб – третьего. Возникает вопрос: при каких ценах у₁, у₂, у₃ мы можем согласиться с предложением.

Величины у₁, у₂, у₃ принято называть расчетными, или двойственными, оценками ресурсов. Они прямо зависят от условий, в которых действует наше предприятие.

В моей задаче технологическая матрица А, вектор объемов ресурсов В и вектор удельной прибыли С имеют вид:

 

2 3 4 1 103

A = 4 2 0 2 B= 148 C= (36 32 10 13)

2 8 7 0 158

 

 

Для производства единицы продукции первого вида необходимо затратить, как видно из матрицы А, 2 единицы ресурса первого вида, 4 единицы ресурса второго вида и 2 единиц третьего (элементы первого столбца матрицы). В ценах у₁, у₂, у₃ затраты составят 2 у₁ + 4у₂ + 2у₃, т.е. столько заплатит предприниматель за все ресурсы, идущие на производство единицы первой продукции. На рынке за единицу первой продукции мы получили бы прибыль 36 руб. Следовательно, мы можем согласиться с предложением П только в том случае, если он заплатит не меньше

2у₁ + 4у₂ + 2у₃ ³ 36

 

Аналогично, во втором столбце матрицы А указаны затраты различных ресурсов на производство единицы продукции второго вида. Эти затраты составят 3 у₁ + 2у₂ + 8у₃, а на рынке за единицу продукции второго вида мы получили бы прибыль 32 руб. Поэтому перед предпринимателем ставится условие

3у₁ + 2у₂ +8у₃ ³ 32

и так далее по всем видам продукции.

За все имеющиеся у нас ресурсы нам должны заплатить 103у₁ + 148у₂ + 158у₃ рублей. При поставленных нами условиях предприниматель будет искать такие значения величин у₁, у₂, у₃, чтобы эта сумма была как можно меньше. Подчеркнем, что речь идет не о ценах, по которым мы когда-то приобретали эти ресурсы, а об этих ценах, которые существенно зависят от применяемых нами технологий, объемов ресурсов и от ситуации на рынке.

Таким образом, проблема определения расчетных оценок ресурсов приводит к задаче линейного программирования: найти вектор двойственных оценок:

 

y (у₁, y₂, y₃)

 

минимизирующий общую оценку всех ресурсов

 

W= 103у₁ + 148у₂ + 158у₃ →min (1)

 

при условии, что по каждому виду продукции суммарная оценка всех ресурсов, затрачиваемых на производство единицы продукции, не меньше прибыли, получаемой от реализации единицы этой продукции

2у₁ + 4у₂ + 2у₃ ³ 36

3у₁ + 2у₃ + 2у₃ ³ 32 (2)

4у₁ + 0у₂ + 7у₃ ³ 10

1у₁ + 2у₂ + 0у₃ ³ 13

 

причем оценки ресурсов не могут быть отрицательными

 

y₁ 0, y₂ 0, y₃ 0 (3)

 

Решение полученной задачи легко найти с помощью второй основной теоремы двойственности, согласно которой для оптимальных решений

=(х₁, х₂, х₃, х₄) и =(y₁, y₂, y₃ )

пары двойственных задач необходимо и достаточно выполнение условий

 

х₁ (2у₁ + 4у₂ + 2у₃ – 36) = 0

х₂ (3у₁ + 2у₂ + 2у₃ – 32) = 0

х₃ (4у₁ + 0у₂ + 7у₃ - 10) = 0

х₄ (1у₁ + 2у₂ + 0у₃ – 13) = 0

 

 

y₁ (2у₁ + 3у₁+ 4у₁ +1у₁ - 103) = 0

y₂ (4у₂ + 2у₃+0у₂ + 2у₂ - 148) = 0

y₃ (2у₃ + 2у₃ +7у₃ + 0у₃ - 158) = 0

 

Так как x₁ > 0 и x₂ > 0, то

2у₁ + 4у₂ + 2у₃ – 36 = 0

3у₁ + 2у₂ + 2у₃ – 32 = 0

 

Если учесть, что первый ресурс был избыточным, то у₂ = 0, и мы приходим к системе уравнений

2у₁ + 2у₃ – 36 = 0

3у₁ + 2у₃ – 32 = 0

 

откуда следует у₁=-4, у₃=22.

 

Таким образом, получили двойственные оценки ресурсов

 

у₁=-4; у₂=8; у₃=2, (4)

 

причем общая оценка всех ресурсов равна 1500.

Решение (4) содержалось в последней строке последней симплексной таблицы исходной задачи. Важен экономический смысл двойственных оценок. Например, двойственная оценка второго ресурса у₁=4 показывает, что добавление одной единицы 1-го ресурса обеспечит прирост прибыли в 4 единицы.

 

 

Задача о "расшивке узких мест производства"

При выполнении оптимальной производственной программы второй и третий ресурсы используются полностью, т.е. образуют ²узкие места производства². Будем их заказывать дополнительно. Пусть T (t₁, t₂, t₃) – вектор дополнительных объемов ресурсов. Так как мы будем использовать найденные двойственные оценки ресурсов, то должно выполняться условие:

H + Q ^-1T 0.

Задача состоит в том, чтобы найти вектор T (0, t₂, t₃), максимизирующий суммарный прирост прибыли

W = 8t₂ + 2t₃ (1)

 

при условии сохранения двойственных оценок ресурсов (и, следовательно, структуры производственной программы)

 

(2)

 

предполагая, что можно надеяться получить дополнительно не более 1/3 первоначального объема ресурса каждого вида

 

t₁ 316

0 <=1/3* 216 (3)

t₃ 199

 

По смыслу задачи t₁ ³ 0, t₃ ³ 0

 

 

28 + 1/28*t₁ ³ 0

7 - 4/7*t₁ - 1/7*t₃ ³ 0

23 –3/28*t₁ + 2/7 t₃ ³ 0

t₁ £ 316/3

t₃ £ 199/3

 

t₁ ³ -784

4/7*t₁ + 1/7*t₃ £ 7

–3/28*t₁ + 2/7 t₃ ³ 23

t₁ £ 316/3

t₃ £ 199/3

t₁ ³ 0, t₃ ³0

 

 

 

 

 

 

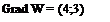
Находим координаты точки А(t1,t2). t₁ = 0, t₂ =49, и прирост прибыли составляет 0*4+49*3=147 рублей.

 

 

cj

b

x4+i

yi

ti

aij

-3/28

2/7

xj

Dj

 

 

Транспортная задача линейного программирования

 

Транспортная задача формулируется следующим образом. Однородный продукт, сосредоточенный в m пунктах производства (хранения) в количествах а₁, а₂,... а_m единиц, необходимо распределить между n пунктами потребления, которым необходимо соответственно b₁, b₂,... b_n единиц. Стоимость перевозки единицы продукта из i-го пункта отправления в j-ый пункт назначения равна с_ij и известна для всех маршрутов. Необходимо составить план перевозок, при котором запросы всех пунктов потребления были бы удовлетворены за счет имеющихся продуктов в пунктах производства и общие транспортные расходы по доставке продуктов были минимальными.

Для решения транспортной задачи чаще всего применяется метод потенциалов.

 

Пусть исходные данные задачи имеют вид:

2 3 4 1

А(40, 60, 70) В (36; 32; 40; 53); С = 4 2 1 2

2 7 7 1

 

Общий объем производства åа _i = 40+60+70 = 170; требуется всем потребителям åb_i = 36+32+40+53 = 161, т.е. имеем открытую модель транспортной задачи. Для превращения ее в закрытую вводим фиктивный пункт потребления с объемом потребления 170-161 = 9 единиц, причем тарифы на перевозку в этот пункт условимся считать равными нулю, помня, что переменные, добавляемые к левым частям неравенств для превращения их в уравнения, входят в функцию цели с нулевыми коэффициентами.

Первое базисное допустимое решение легко построить по правилу ²северо-западного угла².

 

Потребление	b1 = 36	b2 = 32	b3 = 40	b4 = 53	b5 = 9
Производство
а1 = 40					*	p1 =0
a2 = 60						p2
a3 = 70						p3
	q1	q2	q3	q4	q5

 

Следует иметь в виду, что по любой транспортной таблице можно восстановить соответствующий предпочитаемый эквивалент системы уравнений, в таблице записаны лишь правые части уравнений, причем номер клетки показывает, какая неизвестная в соответствующем уравнении является базисной. В любой транспортной таблице должно быть m + n - 1 занятых клеток.

 

Обозначим через m ) вектор симплексных множителей или потенциалов. Тогда D_ij = mA_ij - с_ij

i = 1,m; j = 1,n

 

откуда следует

D_ij = p_i + q_j - c_ij i = 1,m; j = 1,n

Один из потенциалов можно выбрать произвольно. Положим, что р₁ = 0. Остальные потенциалы находим из условия, что для базисных клеток . В данном случае получаем

D₁₁ = 0, p₁ + q₁ - c₁₁ = 0, 0 + q₁ - 2 = 0, q₁ = 2

D₁₂ = 0, p₁ + q₂ - c₁₂ = 0, 0 + q₂ -3 = 0, q₂ = 3

D₂₂ = 0, p₂ + q₂ - c₂₂ = 0, р₂ +3 - 2 = 0, р₂ = 1

D₂₃ = 0, p₂ + q₃ – c₂₃ = 0, 1 + q₃ - 1 = 0, q₃ = 0

D₃₃ = 0, p₃ + q₃ – c₃₃ = 0, р₃ + 0 - 7 = 0, p₃ = 7

D₃₄ = 0, p₃ + q₄ – c₃₄ = 0, 7 + q₄ - 1 = 0, q₄ = 6

D₃₅ = 0, p₃ + q₅ – c₃₅ = 0, 7 + q₅ - 0 = 0, q₅ = -7

 

Затем по формуле

D_ij = p_i + q_j - c_ij i = 1, m; j = 1, n

 

 

вычисляем оценки всех свободных клеток:

 

D₂₁ = p₂ + q₁ - c₂₁ = 1 + 2 - 2 = 1

D₃₁ = p₃ + q₁ - c₃₁ = 7 + 2 - 2 = 7

D₃₂ = p₃ + q₂ - c₃₂ = 7 + 3 - 7 = 3

D₁₃ = p₁ + q₃ – c₁₃ = 0 + 0 - 4 = -4

D₁₄ = p₁ + q₄ – c₁₄ = 0 + 6 - 1 = 5

D₂₄ = p₂ + q₄ – c₂₄ = 1 + 6 - 2 = 5

D₁₅ = p₁ + q₅ – c₁₅ = 0 - 7 - 0 = -7

D₂₅ = p₂ + q₅ – c₂₅ = 1 - 7 - 0 = -6

 

Находим наибольшую положительную оценку

max (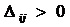) = 7 =D₃₁

Для найденной свободной клетки 31 строим цикл пересчета - замкнутую ломаную линию, соседние звенья которой взаимно перпендикулярны, сами звенья параллельны строкам и столбцам таблицы, одна из вершин находится в данной свободной клетке, а все остальные - в занятых клетках. Это будет 31-11-12-22-23-33. Производим перераспределение поставок вдоль цикла пересчета

 

				36-r	4+r
					28-r	32+r
				r		8-r

 

r_MAX = 8

Получаем второе базисное допустимое решение:

 

Потребление	b1 = 36	b2 = 32	b3 = 40	b4 = 53	b5 = 9
Производство
а1 = 40					*	p1 =0
a2 = 60						p2
a3 = 70						p3
	q1	q2	q3	q4	q5

 

Находим новые потенциалы, новые оценки.

 

D₁₁ = 0, p₁ + q₁ – c₁₁ = 0, 0 + q₁ – 2 = 0, q₁ = 2

D₁₂ = 0, p₁ + q₂ – c₁₂ = 0, 0 + q₂ – 3 = 0, q₂ = 3

D₂₂ = 0, p₂ + q₂ – c₂₂ = 0, р₂ + 3 – 2 = 0, р₂ = 1

D₂₃ = 0, p₂ + q₃ – c₂₃ = 0, 1 + q₃ – 1= 0, q₃ = 0

D₃₃ = 0, p₃ + q₃ – c₃₃ = 0, р₃ + 0 – 7 = 0, p₃ = 7

D₃₄ = 0, p₃ + q₄ – c₃₄ = 0, 7 + q₄ - 1 = 0, q₄ =-6

D₁₅ = 0, p₁ + q₅ – c₁₅ = 0, 0 + q₅ - 0 = 0, q₅ = 0

 

D₂₁ = p₂ + q₁ - c₂₁ = 1 + 2 – 4 = -1

D₃₁ = p₃ + q₁ - c₃₁ = 7 + 2 – 2 = 7

D₃₂ = p₃ + q₂ - c₃₂ = 7 + 3 – 7 = 3

D₁₃ = p₁ + q₃ – c₁₃ = 0 + 0 – 4 = -4

D₁₄ = p₁ + q₄ – c₁₄ = 0 - 6 – 1 = -7

D₂₄ = p₂ + q₄ – c₂₄ = 1 - 6 – 2 = -7

D₂₅ = p₂ + q₅ – c₂₅ = 1 + 0 – 0 = 1

D₃₅ = p₃ + q₅ – c₃₅ = 7 + 0 – 0 = 7

 

Находим наибольшую положительную оценку

max (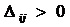) = 7 =D₃₁

 

 

Для найденной свободной клетки 31 строим цикл пересчета 11-31-14-34. Производим перераспределение поставок вдоль цикла пересчета

 

			28-r	r
			8+r	53-r

 

r_MAX = 28

 

Потребление	b1 = 36	b2 = 32	b3 = 40	b4 = 53	b5 = 9
Производство
а1 = 40					*	p1 =0
a2 = 60						p2
a3 = 70						p3
	q1	q2	q3	q4	q5

 

Находим новые потенциалы, новые оценки.

 

D₁₁ = 0, p₁ + q₁ – c₁₁ = 0, 0 + q₁ – 2 = 0, q₁ = 2

D₁₂ = 0, p₁ + q₂ – c₁₂ = 0, 0 + q₂ – 3 = 0, q₂ = 3

D₂₂ = 0, p₂ + q₂ – c₂₂ = 0, р₂ + 3 – 2 = 0, р₂ = 1

D₂₄ = 0, p₂ + q₄ – c₂₄ = 0, 1 + q₄ – 2 = 0, q₄ = 1

D₃₄ = 0, p₃ + q₄ – c₃₄ = 0, p₃ + 1 - 1 = 0, p₃ = 0

D₃₃ = 0, p₃ + q₃ – c₃₃ = 0, 0 + q₃ – 7 = 0, q₃ = 7

D₁₅ = 0, p₁ + q₅ – c₁₅ = 0, 0 + q₅ - 0 = 0, q₅ = 0

 

D₂₁ = p₂ + q₁ - c₂₁ = 1 + 2 – 4 = -1

D₃₁ = p₃ + q₁ - c₃₁ = -2 + 2 – 2 = -2

D₃₂ = p₃ + q₂ - c₃₂ = 0 + 3 – 7 = -4

D₁₃ = p₁ + q₃ – c₁₃ = 0 + 7 – 4 = -3

D₁₄ = p₁ + q₄ – c₁₄ = 0 - 1 – 1 = -2

D₂₃ = p₂ + q₃ – c₂₃ = 1 + 7 – 1 = -7

D₂₅ = p₂ + q₅ – c₂₅ = -3 + 0 – 0 = -3

D₃₅ = p₃ + q₅ – c₃₅ = 0 + 0 – 0 = 0

 

Я получил таблицу, для которой все D_ij £ 0 i = 1,m; j = 1,n

Оценки удовлетворяют условию оптимальности, следовательно решение

 

оптимально.