Рассмотрим пример игры с платежной матрицей размера 4х5:
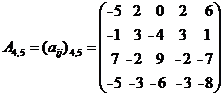
Вначале проведем анали на доминирование. 1-ая строка доминирует j-ю, если все элементы i-ой строки больше или равны соответствующих элементов j-ой. Так как строки выбирает Первый игрок, то мы исключаем из платежной матрицы доминируемые строки. В нашем примере 1-ая строка доминирует 4-ую. В результате ее исключения получим:
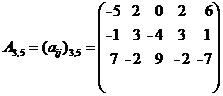
Четвертый столбик доминирует второй и, так как столбцы выбирает Второй игрок, то мы исключаем доминирующий четвертый столбец. В результате получим платежную матрицу 3x4, которую упростить уже невозможно
αi
-5
-4
-7
βj 7 3 9 6
Далее проведем анализ игры на седловую точку. Находим минимумы по строкам α. Тогда нижняя цена игры α=-7.
Находим максимумы по столбцам β. Тогда верхняя цена игры β=9.
Поскольку α ≠β, то решения игры в чистыз стратегиях нет. Бужем искать решение в смешанных стратегиях. Предварительно прибавим к каждому элементу платежной матрицы константу, равную 7, сделав их неотрицаельными. Решение игры при этом не изменится, а цена игры возрастет на 7 и будет больше нуля.
Матрица игры примет следующий вид:
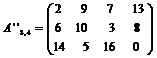
В силу теоремы Неймана решение игры сводится к нахождению решений симметричной пары взаимно двойственных задач линейного программирования. Пусть P=(p1;p2;p3); Q=(q1;q2;q3;q4) – стратегии игроков. Найдем сначала Q*
Если Второй игрок применяет свою оптимальную стратегию, то Первый игрок не может улучшить свое положение, отступая от своей оптимальной стратегии. Заставим Первого отступать от своей оптимальной стратегии, пользуясь чистыми стратегиями p1,p2,p3 (а второй игрок, между тем, придерживается своей оптимальной стратегии Q*). В любом случае проигрыш Второго игрока будет не больше, чем цена игры v
|
|
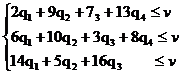
Разделим каждое из неравенств на v>0 и введем обозначения
=xi ≥0
Получим
Поскольку 
, то переменные x1,x2,x3,x4 удовлетворяют условию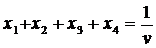 
Но v есть проигрыш Второго игрока, который он стремится сделать минимальным. Следовательно, величина 1/v должна быть максимальна. Таким образом, имеем следующую задачу линейного программирования.
Найти вектор x=(x1,x2,x3,x4), который обеспечивает максимум целевой функции
Z=x1+x2+x3+x4→max
при следующих линейных ограничениях:
x1,x2,x3,x4≥0
После приведенной задачи к основной задаче линейного программирования найдем ее оптимальное решение симплексным методом
X*=(0;1/28;1/14;1/28), при значении целевой функции Zmax=1/7.
Найдем теперь оптимальную стратегию P* первого игрока. Если Первый игрок применяет свою оптимальную стратегию, то Второй игрок не может улучшить свое положение, отступая от своей оптимальной стратегии. В случае использования Вторым игроком своих чистых стратегий Q1,Q2,Q3,Q4, а Первым игроком своей оптимальной стратегии P*, выйгрыш первого будет не меньше чем цена игры:
Разделим каждое неравенство на v>0 и введем обозначения
=yi ≥0
Получим
Поскольку 
, то переменные y1,y2,y3,y4 удовлетворяют условию
y1+y2+y3=1/v.
Но v есть выйгрыш Первого игрока, который стремится его максимизировать. Следовательно, величина 1/v должна быть минимальна. Таким образом имеем слкдующую задачу линейного программирования.
Найти вектор y=(y1,y2,y3), который обеспечивает минимум целевой функции
|
|
L=y1+y2+y3→min
При следующих линейных ограничениях:
y1,y2,y3≥0
Эта задача является двойственной по отношению к рассмотренной выше задаче. Решение задачи возьмем из последней симплексной таблицы:
Уопт=(1/28, 1/14, 1/28); Lmin=Zmax=1/7
Откуда цена игры v0 по-прежнему равна 7.
Далее найдем P*=v0*Уопт=(1/4; 1/2; 1/4)
Возвращаемся теперь к исходной матрице игры A4,5. Решение этой игры имеет вид
v0=0; P*=(1/4; 1/2; 1/4; 0); Q*=(0;1/4; 1/2; 0; 1/4)
Найдем риск игры при использовании игроками своих оптимальных стратегий
а также риск при использовании одним из игроков своей чистой, а другим — своей оптимальной стратегии (нижний индекс Первого игрока, верхний — Второго игрока):
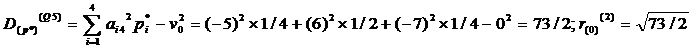
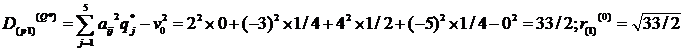
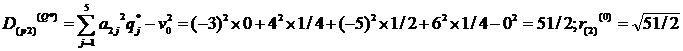
Минимальное значение риска равно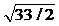 
и меньше r0. Этот риск соответствует ситуациям, когда Первый игрок играет по оптимальной стратегии P*, а Второй игрок использует вторую чистую стратегию Q2; или, когда Первый игрок использует свою первую чистую стратегию P1, а Второй — оптимальную Q*. Однако играть с таким риском, как отмечалось выше, можно только с согласия обеих игроков, т.е. При их сотрудничестве друг с другом.