Распределение капитальных вложений
Динамическое программирование - это вычислительный метод для решения задач управления определенной структуры. Данная задача с n переменными представляется как многошаговый процесс принятия решений. На каждом шаге определяется экстремум функции только от одной переменной.
Предположим, что указано n пунктов, где требуется построить или реконструировать предприятия одной отрасли, для чего выделено b рублей. Обозначим через fi(xi) прирост мощности или прибыли на j-м предприятии, если оно получит xi рублей капитальных вложений. Требуется найти такое распределение (x1,x2,..., xn) капитальных вложений между предприятиями, которое максимизирует суммарный прирост мощности или прибыли
z = f1(x1) + f2(х2) +... + fn(xn)
при ограничении по общей сумме капитальных вложений
x1 + x2 +... + xn = b
причем будем считать, что все переменные xj принимают только целые неотрицательные значения.
Функции fj(xj) считаются заданными. Воспользуемся методом динамического программирования для решения этой задачи.
Производственное объединение состоит из четырех предприятий (n=4). Общая сумма капитальных вложений равна 700 тыс. рублей (b=700), выделяемые предприятиям суммы кратны 100 тыс. рублей. Значения функций fj(xj) приведены в таблице 1, где, например, число 44 означает, что если третье предприятие получит 400 тыс. руб. капитальных вложений, то прирост прибыли на этом предприятии составит 44 тыс. руб.
Таблица 1
| xj | ||||||||
| f1 (x1) | ||||||||
| f2 (x2) | ||||||||
| f3 (x3) | ||||||||
| f4 (x4) |
Прежде всего заполняем табл. 2. Значения f2(x2) складываем со значениями F1(x - x2) = f1(x- x2) и на каждой северо-восточной диагонали находим наибольшее число, которое отмечаем звездочкой и указываем соответствующее значение 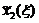 . Заполняем таблицу 3.
. Заполняем таблицу 3.
Продолжая процесс, табулируем функции F3(x), 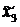 (x) и т.д. В табл. 6 заполняем только одну диагональ для значения x= 700. Наибольшее число на этой диагонали:
(x) и т.д. В табл. 6 заполняем только одну диагональ для значения x= 700. Наибольшее число на этой диагонали:
Zmax = 89 тыс. руб.,
причем четвертому предприятию должно быть выделено
х*4 = 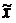 4 (700) = 100 тыс. руб.
4 (700) = 100 тыс. руб.
На долю остальных трех предприятий остается 600 тыс. руб. Из табл. 5 видно, что третьему предприятию должно быть выделено
x*3 = 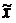 3 (700-x*4) =
3 (700-x*4) = 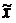 3 (600) = 200 тыс. руб.
3 (600) = 200 тыс. руб.
Продолжая обратный процесс, находим
x*2 = 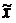 2 (700 - x*4 - x*3) =
2 (700 - x*4 - x*3) = 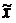 2 (400) = 300 тыс. руб.
2 (400) = 300 тыс. руб.
На долю первого предприятия остается
x*1 = 700 - x*4 - x*3 - x*2 = 100 тыс. руб.
Таким образом, наилучшим является следующее распределение капитальных вложений по предприятиям:
x*1 =100; x*2 =300; x*3 = 200; x*4 = 100.
Оно обеспечивает производственному объединению наибольший воможный прирост прибыли 89 тыс. руб.
 Таблица 2
Таблица 2
| x - x2 | 0 100 200 300 400 500 600 700 | ||
| x2 | F1(x - x2) f2(x2) | 0 15 24 30 36 40 43 45 | |
 0 0
| 0 15 24 30 36 40 43 45 | ||
| 18 2342 48 54 58 61 | |||
| 26 41 5056 62 66 | |||
| 34 4958 64 70 | |||
| 39 54 63 69 | |||
| 42 57 66 | |||
| 44 61 | |||
| 46. |
Таблица 3
| x | 0 100 200 300 400 500 600 700 | |
| F2(x) | 0 18 26 42 50 58 64 70 | |
` 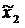 (x) (x)
| 0 100 200 100 200 300 300 300 |
Таблица 4
| x - x3 | 0 100 200 300 400 500 600 700 | ||
| x3 | F2(x - x3) f3(x3) | 0 18 26 42 50 58 64 70 | |
 0 18 26 42 50 58 64 70 0 18 26 42 50 58 64 70
| |||
| 16 34 42 5866 73 80 | |||
| 27 45 53 69 77 85 | |||
| 37 55 63 79 87 | |||
| 44 62 70 86 | |||
| 48 66 74 | |||
| 50 68 | |||
| 56. |
Таблица 5
| x | 0 100 200 300 400 500 600 700 | |
| F3(x) | 0 18 34 45 58 69 79 87 | |
`  (x) (x)
| 0 0 100 200 100 200 300 300 |
Таблица 6

| x - x4 | 0 100 200 300 400 500 600 700 | |
| x4 | F3(x - x4) f4(x4) | 0 18 34 45 58 69 79 87 | |
 0 0
| |||
| 41. |