Необходимо найти кратчайший путь между пунктами 0 и 8.


7 11
6 10 9
7 9
11 5 3
















 12 13
12 13
X0 = 0
X1 = +¥ = 3
X2 = +¥ = 6
X3 = +¥ = 12
X4 = +¥ = 13
6 + 7
3 + 11
X5 = +¥ = 15
3 + 12
X6 = +¥ = 16
7 + 12
6 + 10
X7 = +¥ = 18
13 + 5
X8 = +¥ = 21
12 + 11
16 + 9
13 + 9
13 + 5 + 3
15 + 13
Таким образом, кратчайшее расстояние между двумя пунктами 0 и 8 = 6 + 7 + 5 + 3 = 21
Задача о максимальном потоке в сети
Постановка задачи
Рассмотреть задачу о максимальном потоке в сети. Решить конкретную задачу на сети с 8-9 вершинами.
Исходные данные
Определить максимальный поток в сети, изображенной на Рисунке 6 из вершины x0 в вершину x8, где числа на дугах, снабженные стрелками, означают пропускные способности этих дуг в указанных направлениях.
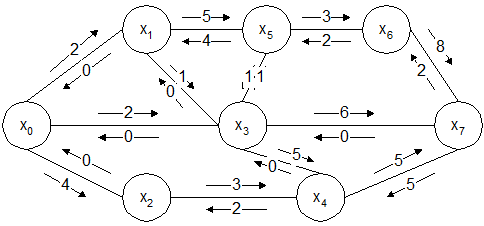 |
Рисунок 6
Решение
Составим матрицу пропускных способностей дуг данной сети и представим сеть в матричной форме (см. Таблицу 1).
 Таблица 1
Таблица 1
| x0xj xi | x1 | x2 | x3 | x4 | x5 | x6 | x7 | |
 x0 x0
| 2- | |||||||
| x1 | ||||||||
| x2 | ||||||||
 x3+ x3+
| 6- | |||||||
| x4 | ||||||||
| x5 | ||||||||
| x6 | ||||||||
| x7 | + |
В качестве начального возьмем нулевой поток z0ij = 0. Найдем какой-нибудь путь, идущий из x0 в x7 по ненасыщенным дугам. Для этого в нулевой строке таблицы выберем какой-нибудь элемент cij, отличный от нуля, например c03. Из вершины x0 можно перейти в x3. Для наглядности дугу (x0, x3) проведем прямо в нулевой строке таблицы из нулевого столбца в 3-й. Теперь мы находимся в вершине x3. Чтобы зафиксировать это, сместимся по пятому столбцу до строки с тем же 3-м номером. В 3-й строке имеется 3 ненулевых элемента соответственно в 4-м, 5-м и 7-м столбцах. Это означает, что из x3 можно перейти или в x4, в x5 или в x7. Пойдем в сток x7. Этот переход изображен стрелкой в 3-й строке с началом в 3-м столбце и концом в 7-м. Таким образом, по таблице пропускных способностей дуг сети мы нашли путь, ведущий по ненасыщенным дугам из источника в сток:
m1 = [x0, x3, x7].
Теперь по таблице надо узнать пропускную способность q1 найденного пути и уменьшить пропускные способности всех дуг этого пути на q1, а симметричных им дуг – увеличить на q1. Для этого отмечаем знаком «-» числа в тех клетках, где находятся концы дуг, а числа в клетках, симметричных указанным относительно главной диагонали, отмечаем знаком «+». Пропускная способность найденного пути, очевидно, равна наименьшему среди чисел, отмеченных знаком «-» (Таблица 1).
q1 = 2
Из всех чисел, отмеченных знаком «-», вычитаем наименьшую пропускную способность q1. Получаем Таблицу 2. Это – сеть с измененными пропускными способностями дуг.
 Таблица 2
Таблица 2
| x0xj xi | x1 | x2 | x3 | x4 | x5 | x6 | x7 | |
 x0 x0
| 4- | |||||||
| x1 | ||||||||
 x2+ x2+
| 3- | |||||||
| x32 | ||||||||
 x4 x4
| 2+ | 5- | ||||||
| x5 | ||||||||
| x6 | ||||||||
| x7 | 5+ |
Ищем новый путь, идущий из источника в сток по ненасыщенным дугам и процедуру повторяем. Получаем путь m2 и пропускную способность q2:
m2 = [x0, x2, x4, x7]
q2 = 3
Далее
 Таблица 3
Таблица 3
| x0xj xi | x1 | x2 | x3 | x4 | x5 | x6 | x7 | |
 x0 x0
| 2- | |||||||
 x1+ x1+
| 5- | |||||||
| x23 | ||||||||
| x32 | ||||||||
| x4 | ||||||||
 x5 x5
| 4+ | 3- | ||||||
 x6 x6
| 2+ | 8- | ||||||
| x7 | 2+ |
m3 = [x0, x1, x5, x6, x7]
q3 = 2
 Таблица 4
Таблица 4
| x0xj xi | x1 | x2 | x3 | x4 | x5 | x6 | x7 | |
| x0 | ||||||||
| x12 | ||||||||
| x23 | ||||||||
| x32 | ||||||||
| x4 | ||||||||
| x5 | ||||||||
| x6 | ||||||||
| x7 |
Из Таблицы 4 видно, что не существует ни одного пути из источника в сток. (Из x0 можно перейти только в x2, а оттуда – обратно в x0). Следовательно, увеличить поток нельзя.
Для определения величины полученного максимального потока вычитаем из элементов Таблицы 1 соответствующие элементы Таблицы 4. Записывая только положительные из найденных разностей, получаем Таблицу 5, указывающую максимальный поток в заданной сети с величиной
w* = z37 + z47 + z67 = q1 + q2 + q3 = 7
 Таблица 5
Таблица 5
| x0xj xi | x1 | x2 | x3 | x4 | x5 | x6 | x7 | |
| x0 | ||||||||
| x1 | ||||||||
| x2 | ||||||||
| x3 | ||||||||
| x4 | ||||||||
| x5 | ||||||||
| x6 | ||||||||
| x7 |